Session 1
SLOs:
- Instantly recognise patterns for teen numbers.
- Make groups of ten and represent teen numbers with materials.
- Recognise and record words and symbols for teen numbers.
Activity 1
- Show the ākonga single tens frames. Have them show the same number of fingers as the number of dots, say and write the number with their finger in the air or on the mat.
- Show two tens frames, one of ten and the other of a number less than ten, together making a teen number. Have ākonga ‘write’ with their finger how many dots they see. For example:

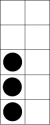 13
13
Repeat with several teen numbers.
- Write the numbers 11 – 19 in symbols and words on chart paper, highlighting the inconsistencies of the language and exploring for fun alternative forms of some of the teen numbers, for example, eleven (oneteen), twelve (twoteen), thirteen (threeteen), fifteen (fiveteen). For each word, as appropriate, underline teen in the word, practice saying it and hearing the final consonant, ‘n’. Make the connection between this ‘teen’ word and ‘ten’. Retain this chart to add to later. This chart could also include words for 'teen' numbers from other languages relevant to your ākonga.
- Ask your ākonga what they notice about all of these numbers. (They all have 'teen' at the end and are ten and ‘something’). They are known as teen numbers.
Activity 2
Have ākonga work in pairs to play Teen Pairs. Consider pairing together ākonga of mixed mathematical abilities to encourage tuakana/teina.
Purpose: to recognise and match teen number representations and the words ‘ ten and ____’
Ākonga place between them two piles of cards face down (Copymaster 1).
Pile 1: Tens frame teen number cards (showing two tens frames).
Pile 2: Word Ten and _____ cards.
Ākonga take turns to turn over one tens frame teen number card and say the number of dots they see. They then turn over a word card and read the words aloud. If the tens frames and word card match, they keep the matching pair. The winner is the ākonga with the most pairs.
For example:


Activity 3
- Have ākonga work in pairs to ‘make’ their own group of ten. Give each pair of ākonga forty ice-block sticks, two elastic hair ties, pens and chart paper or a mini whiteboard.
- Have each ākonga pair choose and write in symbols a number from eleven to nineteen and take that many sticks. Have them count out and make one bundle of ten using the hair tie, then write and draw what they have. For example:



12 is ten and two - Have them unbundle and return their sticks, then repeat with another teen number making use of spare sticks as required.
- Ask the ākonga to return to the whole group with their drawings, keeping them hidden. Have the ākonga take turns to describe to the class what they have drawn, and ask another ākonga to say what number it is. The drawing is then shown.
- The kaiako concludes by recording the ‘ten and _________’ words beside each of the teen numbers on the class chart begun in the earlier activity. Also consider exploring together the Place Value sticks animation, available from https://e-ako.nzmaths.co.nz/modules/PVanimations/
Session 2
SLOs:
- Make groups of ten and represent teen numbers with materials.
- Recognise and record words and symbols for teen numbers.
- Understand that in a teen number, the 1 represents one group of ten
Activity 1
- Have ākonga sit with a partner. Tell them that each pair is going to be making teen numbers on their fingers and ask them to discuss how they will do this. Look and listen for those ākonga who immediately identify that one of their pair will be the ‘ten person’, holding up ten fingers each time.
- Hold up a mixture of cards with number names in words, symbols and those reading ‘ten and ___’. (Copymaster 2). Each time, check to see if ākonga pairs can achieve the cooperative representation on their fingers.
- The kaiako makes a teen number from ice block sticks, having ākonga count to ten as the ten bundle is made.






Hold up the ten bundle and ask, 'Do I still have ten sticks here?' (yes) 'How many bundles of ten do I have?' (1). Record this on the chart, for example, I have fifteen. 15 is ten and five. 15 is 1 ten and 5 ones. Discuss the language of ‘ones’ and that sometimes ‘ones’ can be called ‘units’.
- Model some more examples then have ākonga individually draw and write about some of their favourite teen numbers. For example '12 is 1 ten and two ones'.
Activity 2
If available, have ākonga work in small groups or pairs to explore, find and display the four matching cards in the BSM 9-1-48 card game.
Alternatively, ākonga can make a class puzzle matching game. Provide each ākonga with card, pens and scissors. Have them make their own puzzle pieces which can then be combined with those made by their classmates and mixed up to make a matching pairs game. Before cutting these up, photocopy an extra 3 or 4 sets to be used later on in this unit.
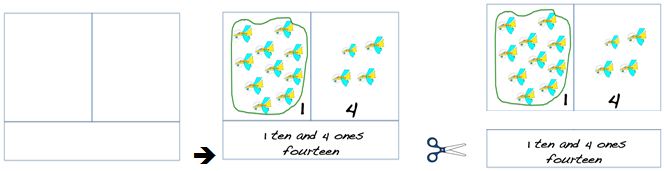
Activity 3
- Return to the class chart started in Session 1. Record te reo Māori words for teen numbers, highlighting ‘tekau mā’ is ‘ten and’, connecting this mathematics language with the other expressions already recorded.
- Photocopy a few more sets of the matching game ākonga made in Session 2, Activity 2. Distribute this game so that your ākonga can play it in small groups of 3-4. The purpose of this game is to match word, pictorial and symbol representations of teen numbers.
Ākonga deal out 7 cards each. The remaining pile of cards is placed in the centre of the group. Ākonga take turns to ask one other player for a card needed to complete a set of 3 teen family cards. If the other player does not have the card sought, the requesting player takes one from the pile. As sets are complete, ākonga place these in front of them.
The winner is the player with the most complete sets.
Session 3
SLOs:
- Understand that in a teen number, the 1 represents one group of ten.
- Expand teen number notation and understand simple place value.
- Understand and apply a ten for one exchange.
Activity 1
- Display the chart started in Session 1. Record beside the numbers 11 – 19 the description ‘1 ten and x ones’ for each of the numbers.
- Using enlarged arrow cards demonstrate and discuss the place value notation that we use, highlighting tens and ones language.


- Introduce ākonga to plastic beans and containers. Have them work in pairs to make up containers with ten beans in each and discuss what the containers will be called. (a container is ‘one ten’ or ‘a ten’). Have ākonga discuss the similarities between the sticks they have been using and the beans.






NB. The container for the beans looks different from the ones, but can still be unpacked. This is a subtle and important shift. Also consider exploring together as a group or class the place value beans animation, available from https://e-ako.nzmaths.co.nz/modules/PVanimations/ - Give ākonga time to become familiar with the beans and the arrow cards. Have them make and model teen numbers with the equipment, explaining this to their partner.
- Have each ākonga complete a think board sheet (Copymaster 3) or a mini poster about one of their favourite teen numbers. Display these.
Activity 2
Ākonga play Go Teen in pairs. A tuakana/teina model could work well here.
Purpose: to use ten ones to make one group of ten, when adding two single-digit numbers.
Ākonga have playing cards (ace - 9), shuffled and face down between them. Alternatively you could print out numeral cards 1-9. They have single beans and empty tens containers (or single ice block sticks and hair ties), single digit and tens arrow cards available.
The players take turns to turn over two playing cards. When the two numbers are added, if they make less than ten they return them face down to a discard pile.
If they make more than ten they keep their playing cards, take the total number of beans, group the materials showing the total as 1 ten and units. They also show the number with the arrow cards.
However, if the number has already been made by their partner, (the arrow cards for that number have been used) the ākonga must simply return their playing cards to the discard pile.
The winner is the player with the most tens (containers with beans) when all the arrow cards have been used up.
Session 4
SLOs:
- Understand and apply a ten for one exchange.
- Understand how to decompose a ten in order to subtract.
Activity 1
- Kaiako models a teen number with containers and beans and asks, ‘What number is shown here?’. For example, 18:









A problem is posed in which the number being subtracted requires the ten to be ‘unpacked’ or decomposed:
'Here are the beans Gardener Gavin is going to plant. He plants 9 in the first row. How many beans are left to plant in the second row? How can we work this out?'
Ākonga can discuss strategies for subtracting 9 and suggest what they can do with the materials. Kaiako models this and some more examples can be explored together.
- Ākonga are provided with place value materials and are each given some subtraction problems to solve with decomposition (Copymaster 4). Ākonga should record with pictures, words and an equation what they did and what their result is. The thinkboard (Copymaster 3) could be used again - it could be laminated and be reusable with a whiteboard pen.
- Share as a class and discuss. The language of making ten (composing) and breaking ten (decomposing) can be introduced.
Activity 2
- The kaiako asks a ākonga to model twenty using place value material. Discuss what this represents: two tens is the same as twenty. Rua tekau is a good example of this concept.
- Have the ākonga play in pairs or small groups First to twenty.
Purpose: to understand how to compose and decompose a ten.
Equipment: Ākonga beans and containers, numeral cards 11- 14, a set of playing cards 2 – 5, a dice with a + or – symbol marked on each of the six faces, mini whiteboards and markers.
How to play:- Numeral cards are spread out face down.
- Each ākonga selects a card and makes that number using place value equipment.
- Players take turns to roll the dice and turn over a playing card. They follow the instructions on the card, either adding or subtracting from their materials.
- Each time an ākonga has a turn they are required to write the equation.
- The winner is the first ākonga who has two containers of ten beans (twenty).
For example: one ākonga turns over and models 13, rolls + and 3, and makes 16.
At their next turn the ākonga may have to – 4, followed on the next turn by – 3.
This will require the ākonga to decompose the ten.
The ākonga will have recorded for the three turns so far:
13 + 3 = 16
16 – 4 = 12
12 – 3 = 9
Conclude the lesson with a focus on the words, ‘place value’. The kaiako writes ‘place value’ on a chart and asks ākonga what this could mean. They are encouraged to look at all the recording of teen numbers completed throughout these lessons. Accept all responses, but conclude by highlighting and recording that 'the place of a numeral in a number tells us what it is worth or its value.' Show the enlarged arrow cards drawing attention to the words tens and ones.


All about us
This unit provides you with a range of opportunities to assess the entry level of achievement of your students.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
The context for this unit can be adapted to suit the interests and experiences of your students. For example:
Prior Experience
It is expected that students will present a range of prior experience of working with numbers, geometric shapes, measurement, and data. Students are expected to be able to count a small set of objects by ones, at least.
Session One
In this first session students explore an activity called ‘Handfuls' which was first developed by Ann Gervasoni from Monash University, Melbourne. Handfuls could become a regular part of lessons during the year.
How can we check how many things there are?
Session Two
In this session, called “Our Favourites” students explore category data and how it might be displayed. The data comes from their responses, so the displays provide useful information about the class. You may wish to replace the images provided in Copymaster 1 with images of sports that you know are popular with your students.
If we want to find out the favourite sport, what could we do?
Could we arrange the squares, so it is easier to see which sport has the most and the least squares?
The students will now choose other ‘favourites’ to use as data. Copymaster 2 provides some strips of favourites including favourite fruit, fast food, pet, vegetable, way to travel to school, and after school pastime. You may wish to create your own strips using ‘favourites’ that are relevant to your group of students.
Session Three
In this session your students use the language of two-dimensional shapes to provide instructions to other students. The use of te reo Māori vocabulary for shapes could also be introduced and used within this session.
You need multiple sets of shapes. Ideally there is a set of shapes for each pair or trio of students. Attribute blocks are used below to illustrate the activity but other shape-based materials such as those below are equally effective.
“Make Me” is an activity that can be used throughout the year with different materials to develop your students’ fluency in using geometric language for shape and movement.
Where could I put the mirror, but it still looks like the whole shape?
Use two shapes positioned together to draw out the language of position. For example:
right side of the square.
Look to see whether your students:
Session Four
In this session students compare items by mass (weight).
How could we find out which thing is heavier?
Students usually suggest that the objects can be compared by hefting, that is holding one object in each hand.
What can we say about the weight of these two objects?
Look for statements like, “The book is heavier than the stapler,” or “The stapler is lighter than the book.”
Let’s put these objects in order of weight. Who thinks they could do that?
I want you to find five things from around the classroom and put them in order of weight. You can use hefting if you want but we have other balances you can use. You will need to record for us, so we know the order of the objects.
Look to see if your students can:
Session Five
In this session students look for repeating patterns and connect elements in the pattern with ordinal numbers.
Dear parents and caregivers,
For the first week of school our mathematics unit is about us. We will investigate efficient ways to count a set of objects, create graphs of data about ourselves, order objects by mass (weight), build models of shapes from instructions, and create our own sequential patterns.
Making ten
The purpose of this unit of sequenced lessons is to develop knowledge and understanding of combinations to ten.
These lessons build upon the student’s recognition and knowledge of groupings within ten, to scaffold ready combinations and separations in numbers that make ten.
A goal within primary mathematics is for students to use partitioning strategies when operating on numbers. By building images and knowledge of these combinations at an early age, the ability to naturally partition larger numbers will be strengthened. Students should have many opportunities to combine and separate numbers to ten and come to clearly see and understand how these ‘basic facts’ are fundamental building blocks of our number system.
As they work with numbers greater than ten, students will develop knowledge of ‘tidy numbers’ and about ‘rounding to ten’. Students should be encouraged to know and have an intuitive feeling for "ten". Ultimately, they should be able to readily apply this knowledge in solving problems that involve partitioning and combining larger numbers and sets.
Our place value system has ten digits only. It is the place of a digit in a number that determines its value. Ten is the basis of this system. By having the opportunity to briefly explore other number systems (Roman and Mayan), and by considering notation to create their own system, students will better understand the numerals and number representations that we may take for granted within the base ten system we use.
The activities suggested in this series of lessons can form the basis of independent practice tasks.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
The contexts for this unit can be adapted to suit the experiences of your students. For example, numbers to ten in other languages can be used in this unit in response to the languages and cultures of your students. For example: numbers from Pasifika cultures could be included in a similar way to how te reo Māori is used in session 4.
Te reo Māori vocabulary terms such as mati (digit) and meka matua (basic facts) could be introduced in this unit and used throughout other mathematical learning.
Session 1
SLO: Explore the numerals to ten.
Activity 1
Activity 2
Sessions 2-3
SLOs:
Introduce the following activities over the next two sessions.
Activity 1
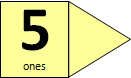
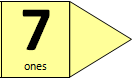
Have the students show ten on their fingers, then have them describe to a partner how many dots they see and how many fingers they see, using ‘ten and no more.’ Record 10 + 0 = 10
Record equations with unknowns representing some of the tens frames; For example, for dots: 7 + ☐ = 10, 10 = 4 + ☐, 10 = 1 + ☐
Make it clear that the spaces ask us ‘how many more to make ten?’
Record equations, 7 + 3 = 10 and 3 + 7 = 10.
Ask what subtraction equations can be recorded using these numbers. Accept student responses, write and model by removing counters, 10 – 3 = 7 and 10 – 7 = 3
Highlight that the four equations are related because they use the same 3 numbers. They are known as a family of facts.
Model with other tens frames: for example 10 = 4 + 6, 6 + 4 = 10, 10 – 4 = 6 and 10 – 6 = 4.
Students say, “Eight,” and write 2. Students with emergent writing skills could be paired with a student with more developed writing skills, or could use counters to demonstrate their understanding of how many more are needed to make ten.
Activity 2
Students play Clever Fingers in pairs. (Purpose: to practice seeing, saying and writing combinations to ten)
They need ten counters, pencil and paper to record winning equations. For each “hand” played they move a counter into a ‘used’ pile.
Students, with their hands behind their backs, make a number on their fingers.
They take turns to call ‘Go.’ On ‘Go’ they show their fingers. If the combination of raised fingers makes ten, they say, “Clever fingers” and one student records the equation. 3 + 7 = 10 When all the counters are used (they have had ten turns). They count their equations. Student pairs compare results.
Activity 3
Students play Snap for Ten in pairs.
(Purpose: to practice seeing, saying combinations to ten)
They need playing cards with Kings and Jacks removed, and use the Queen as a zero.
Turn over a card to begin the game.
Students take turns to turn over a card from the pack, placing the turned card on top of the card before. If the turned card can combine in some way with the previous card to make ten the student says, ‘Snap’, states the equation and collects the pile of cards.
For example: if 9 is turned, followed by a 1, 9 + 1 = 10 is stated and the pile of cards is collected.
Activity 4
Students play Memory Tens in pairs..
(Purpose: to practice seeing and saying combinations to ten)
They need playing cards with Kings and Jacks removed, and use the Queen as a zero.
Cards are turned down and spread out in front of the students.
Students take turns to draw pairs. If the numbers on the two cards combined make ten, the pair is kept by the player.
For example: A player draws 6 and 4 and states 6 + 4 = 10 and keeps the pair.
The game continues till all cards are used up.
The winner is the person with the most pairs.
Activity 5
Students play Fast Families
(Purpose: to practice writing and demonstrating family of fact combinations to ten)
They need pencil and paper.
Students place ten counters of one colour on a blank tens frame.
They take turns to roll a ten-sided dice. The dice roller removes the number of counters indicated by the dice roll and says, “Go.”
The players quickly write the four family of fact members associated with 10, 6 and 4: beginning with the equation just modeled.
10 – 6 = 4, 6 + 4 = 10, 10 – 4 = 6, 4 + 6 = 10.
The first to write these calls stop.
That player chooses another player to demonstrate and say the other three family members in logical order by adding 6 onto the 4, saying 4 + 6 = 10, then removing 4 counters saying 10 – 4 = 6 and finally adding 4 back onto the 6 and saying 6 + 4 = 10.
If this player is correct, he rolls the dice and the game begins again.
The winner is the student who accurately records the most families of facts.
Session 4
SLO: Recall and apply groupings to ten using te reo Māori.
If students are unfamiliar with nga tau, have a number chart displayed.
Each student has a set of number words to ten in te reo Māori (Copymaster 1).
A ten-sided dice is passed around the class circle. Each student takes a turn to roll the dice and call the number in English and in Māori and classmates must hold up the Māori word.
(Purpose: to recognise and come to know number words in te reo Māori)
A mixed piles of tens frames are provided with a mixed pile of Māori number word cards to ten.
Both are turned down. The students take turns turning over a tens frame and a word card. If they match they keep the pair.
The winner is the player who has the most pairs when all the cards are used.
(Purpose: to recognise and come to know number combinations to ten using Māori number words)
Each student shuffles a double set of Māori number word cards to ten and places the pile face down in front of them.
They take turns to turn over one word card at a time and place these in one pile, one on top of another. If two consecutive numbers together make ten, the player who played the second card calls, ‘Tekau’ and collects the whole pile and begins the game again.
The winner is the player with all the cards or with the biggest pile when the game is stopped.
Session 5
SLO: Recognise the usefulness of knowing combinations to ten.
Have a set of tens frames displayed to support some students.
Provide each student with a number fan.
As the teacher shows a digit, each student finds and shows the complementary digit to ten.
For example: the teacher shows 3 and each student shows 7.
For example, the teacher writes 10 – 2 = ☐ and the students show 8, the teacher writes ☐ - 5 = 5 and the students show 10.
Ask the students, “What is a fact?” and record their responses. (A fact is something that has really occurred or is actually the case. It is something that can be tested and can be found to be true).
Ask the students, “What does ‘basic’ mean?” and record their responses. (Something that is basic is essential, fundamental. A ‘base’ is the bottom support of anything or the thing upon which other things rest. It is a foundation.)
Session 6
SLOs:
Demonstrate this by developing with the students and “If I know this, then I know that ” flow diagram. For example:
The students are being introduced to this idea. They are not expected to immediately apply the principle to the bigger numbers.
Highlight the important idea that maths is about relationships between numbers, like fact families, and if we look for these and for number patterns, they help us.
Have students complete their own copies of the grid (Copymaster 2) and write (up to) five things they notice.
Have them share with a partner what they have discovered.
Dear parents and whānau,
In class we have been making, saying and practising addition and subtraction facts with numbers up to ten.
Your child can access practice tasks on the e-ako maths website: https://e-ako.nzmaths.co.nz/ if this suits your family arrangements.
Your child would also enjoy sharing with you activities they have learned in class and would appreciate your making time to play a maths games with them. Here are two we have played in class. You might like to make up one of your own too.
Memory Tens.
In pairs, using playing cards with Kings and Jacks removed, and using the Queen as a zero:
Cards are turned down and spread out in front of the players.
Players take turns to draw pairs. If the numbers on the two cards combined make ten, the pair is kept by the player.
For example: A player draws 6 and 4 and states 6 + 4 = 10 and keeps the pair.
The game continues till all cards are used up.
The winner is the person with the most pairs.
Snap for Ten.
In pairs, using playing cards with Kings and Jacks removed, and using the Queen as a zero:
Turn over a card to begin the game.
Players take turns to turn over a card from the pack, placing the turned card on top of the card before. If the turned card can combine in some way with the previous card to make ten the student says, ‘Snap’, states the equation and collects the pile of cards.
For example: if 9 is turned, followed by a 1, 9 + 1 = 10 is stated and the pile of cards is collected.
The winner is the person with the most cards.
Teddy Bears and Friends
In this unit we compare the lengths of ākonga soft toys directly, and then indirectly using non-standard measurement units.
In this unit ākonga begin by making direct comparisons between objects and putting a number of objects into order according to length. They are also introduced to measuring with multi-link cubes which allows them to compare objects which cannot be placed together.
Multi-link cubes are an example of a non-standard measuring unit. They reinforce most of the principles that underpin measurement and allow ākonga to find out that:
Ākonga will also be encouraged to estimate. Initially these estimations may be little more than guesses, but estimating involves ākonga in developing a sense of the size of the unit. The skill of estimating is just as important as finding exact measurements, as both skills are used frequently in everyday life, for example, estimating shoe size before trying on a shoe, knowing exact height to go on a waterslide.
The learning opportunities in this unit can be differentiated by providing or removing support to ākonga and by varying the task requirements. Ways to support ākonga include:
As the focus of this unit is making measurements of themselves it is already in a context that is meaningful. In some situations, it may be more appropriate to use a collection of classroom objects rather than ask students to bring toys to school.
The context for this unit can be adapted to suit the interests and experiences of your ākonga. For example:
Te reo Māori vocabulary terms such as ine (measure), roa (long), poto (short), nui (big) and iti (small) could be introduced in this unit and used throughout other mathematical learning.
In preparation for this unit, ask ākonga to bring a soft toy to kura. Have a supply of soft toys available to use in the classroom (e.g. for ākonga that forget).
Getting Started
Who has a toy that is taller than this?
Who has a toy that is shorter than this?
Who has a toy that is the same height as this?
Exploring
For the next 3 days we make comparisons using ākonga. In pairs, ākonga take turns drawing outlines of their bodies. A tuakana/teina model could work well here. They use these outlines to make measurements using multi-link cubes or cuisenaire rods (the 10 ones work best). Kaiako or ākonga can record their estimates and actual measurements as appropriate.
At the end of each day, share mahi and make comparisons. Remember to make comparisons amongst the same type (toys or ākonga, in this case).
Whose arm measured more than 25 cubes?
How many more?
Which parts of your body were measured shorter than your arm?
Which is your smallest measurement?
Which is your largest measurement?
What have you measured with rods? Why did you choose rods?
Have you ever been to a place where you were measured? Tell us about it.
Reflecting
Today we line up the outlines of our soft toys ready to go to kura assembly with (the shortest in the front.)
Dear family and whānau,
This week at kura we have compared the lengths of different objects including the toys you brought to kura. We would like your child to have a go at ordering their other toys at home, in order of shortest to tallest. Cutlery, food items or clothing could be used instead of toys. Take a photo or draw a picture of your line up and send it to kura for your tamariki to share.
How long now?
In this unit students compare the duration of events and learn to read time to the hour and half-hour.
Duration
Comparing the duration of two events is an important part of developing an understanding of time passing. This can be done by directly comparing two activities that have common starting points, for example, singing a waiata or running around the building.
After ākonga have directly compared the duration of two events we use sand-timers, counting, and other non-standard measures to compare two or more events.
Telling time
In this unit we learn the skills to tell time to the hour and and half-hour. Telling time must enable them to:
The learning opportunities in this unit can be differentiated by providing or removing support to ākonga and by varying the task requirements. Ways to differentiate include:
The contexts for the duration activities are based on activities that are undertaken by ākonga in your classroom so should be engaging to them. Asking ākonga to choose which activities they would like to compare provides further opportunities for their engagement. For example, they could sing a waiata, complete a hand game or do a short obstacle course.
Te reo Māori vocabulary terms such as karaka (clock), karaka mati (digital clock), karaka ringa (analogue clock), haora (hour), and meneti (minute) could be introduced in this unit and used throughout other mathematical learning.
Session 1: Who finishes first?
In this activity we directly compare two activities to see which takes the longest.
Session 2: Clapping time
In this activity we indirectly compare "quick" events by clapping, stamping and linking cubes.
Writing my name 9 claps
Walking to the board 11 claps
Session 3 : A big clock
In this activity ākonga form a large clock which is then used to show hour times. As you need a large space for the "people clock" this may be best done outside.
Session 4: Making Clocks
In this activity ākonga create their own clocks using paper plates and then use the clock to show times during the school day.
Session 5: The best times of the day.
In this activity we look at different kinds of clocks and talk about telling the time. We draw a picture of our favourite time of the day.
Dear parents and whānau,
This week we have been exploring time and learning to tell time to the hour and half-hour. We have also been looking at different sorts of clocks.
Please support your child to draw pictures or take photos of clocks in your home and community (for example, watches, appliance clocks, novelty clocks, clock radios). We will be using these pictures in an activity later in the week so please email them or send them to school.
Another way you can support your child's learning is by talking about the time when certain things happen, especially if it is on the hour or half hour. For example: "Look! It's 8 o'clock, time for bed" or "It's 5:30, time for tea".
Amazing Mazes
This unit introduces some of the key concepts of position and direction in the context of a series of activities around mazes.
At Level 1 the Position element of Geometry consists of gaining experience in using everyday language to describe position and direction of movement, and interpreting others’ descriptions of position and movement. In this unit students will gain experience using the language of direction, including up, down, left, right, forwards, backwards in the context of mazes. For more activities that involve students giving and following instructions using the language of position and direction you might like to try Directing Me.
Spatial understandings are developed around four types of mathematical questions: direction (which way?), distance (how far?), location (where?), and representation (what objects?). In answering these questions, students need to develop a variety of skills that relate to direction, distance, and position in space.
Teachers should extend young students' knowledge of relative position in space through conversations, demonstrations, and stories. For example, when students act out the story of the three billy goats and illustrate over and under, near and far, and between, they are learning about location, space, and shape. Gradually students should distinguish navigation ideas such as left and right along with the concepts of distance and measurement.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
The context for this unit can be adapted to suit the interests and experiences of your students by engaging them in identifying the character and destination for each maze. Simple Māori designs can be used for mazes. Images of Native Garden Mazes can be shared with the children to engage them in the unit.
There are many books of mazes and online interactive mazes available. Try to have different resources available in the classroom while you are working on this unit. Early finishers or students who need more challenge could be given the opportunity to work with the other mazes or draw their own.
Session 1
Many students may have some experience of using mazes, whether it is walking through mazes, or solving pen and paper mazes in puzzle books.
Sessions 2-3
Maze Pairs
In this activity one student has a picture of a maze and the other has a blank grid. There are 4 mazes (two basic and two harder), and two blank grids (one for the basic mazes and one for the harder ones) available as copymasters. You can also easily make more mazes by using a vivid to draw walls on the blank grids.
Put Yourself in the Maze
For this extension to Maze Pairs tell students that they have to imagine that they are actually in the maze themselves, and that the only things they can do are to move forward or to turn left or right. This makes the activity much more challenging, as they now need to keep track of the direction they are facing as well as where in the maze they are. Counters with an arrow drawn on to indicate direction faced would be a useful aid.
The activity proceeds as in Maze Pairs above but both partners should use a counter with an arrow as they plot their route through the maze.
Outdoor maze
In this activity students take the direction giving skills they have used in the classroom outside and onto a larger scale.
Session 4
Let students draw their own mazes on grid paper, and challenge a friend to first solve it, and then give instructions for how to get through it. Display some examples of a variety of simple mazes as inspiration.
You may need to give some guidance in drawing mazes – ensure that they are solvable, but try to have plenty of false paths and dead ends.
Possibly students could take their mazes to another class and show them how they have learned to give accurate directions through the maze, or take them home to share with whānau.
Dear family and whānau,
This week we are looking at solving mazes and giving directions in maths. Encourage your child to use language such as left, right, over, under, near, far, to describe where objects are in relation to each other. Ask your child to describe the path they would follow to get out of their room if there was a fire. Ask them to describe the route they take to get to school. Using this kind of language helps to develop the maths ideas. Discuss the terms for left, right, over, under, near, far in your own language.
I Like Toys
In this unit we explore ways to pose and answer investigative questions about our favourites by gathering and analysing data and discussing the results.
In this unit the students begin by brainstorming areas for investigation. Young students' areas of interest are likely to focus on themselves and the activities that they are engaged in. Using the students and their interests is a recurring technique used in junior classes. It provides students with contexts that are meaningful and motivating. With the teacher investigative questions are posed about categorical data.
In this unit we use favourites as the theme for the investigations. Much of the data collected at level one will be real objects. In this unit we begin by posing an investigative question about our favourite toys. Once the data (toys) are collected together they can be sorted into categories ready for display. It is important that the students are involved in deciding how to sort the objects. We then draw pictures of other favourites and use them to make displays.
Once more we stress the importance of letting the students decide how to sort and display the data. In this unit we photocopy the drawings so that each pair of students gets the opportunity to make decisions about how the data should be sorted and displayed. The follow-up discussion of the displays will involve the students making statements about the number of objects in each of the categories. In this unit we do not attempt to get the students to formalise their displays into pictographs. However the thinking carried out in this unit means that the students would be ready to use pictographs in future statistics units.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
The context, about favourites, for this unit can be adapted to suit the interests and experiences of your students by selecting favourites of interest to your students.
A te reo Māori term that can be introduced in this unit is rōpū (group). Counting in te reo Māori could be used throughout the sessions.
Session 1
Let’s try to find out about our favourite toys. The investigative question we are exploring is "What are the favourite toys of the children in our class?"
Do any of you have toys that could belong with this one? Is there some way that your toy is like this one? How does your toy belong? Who has one that doesn’t belong? Why not?
Four of us brought dolls or action men. Three of us brought balls to kick. Six of us brought toys with wheels. Two of us brought soft animals etc
Session 2
In this session we collect sets of data to use in investigations in the following sessions. If you have time available at the end of the session you may wish to start analysing one of the sets.
Possible favourites include: food, colour, drink, number, animal.
Sessions 3 and 4
In preparation for the next two days, make a set of picture sheets for each pair by photocopying the answers from session 2 (8 per sheet of A4). It is worth taking the time to make copies as it gives everyone the opportunity to sort and display the data.
Can you see your drawing?
Do you see any that are like yours?
Which ones are different to yours?
How are you sorting the pictures?
How many categories or groups have you got?
Is it easy to decide where to put the pictures? Why/Why not?
Session 5
We begin today’s session by getting the students to select their favourite investigation to display on the classroom walls.
How many chose that favourite (e.g. fruit)?
Which things are favourites? How do you know? How does your display show that?
Dear parents and whānau,
This week in mathematics and statistics we are exploring ways to pose and answer investigative questions about our favourites by gathering and analysing data and discussing the results. One of our activities involves us investigating our class and families favourite type of fruit. To help us with this activity we would like everyone in your home to draw us a picture of their favourite fruit. Your child will then add this to our display that shows the favourite fruits. We are answering the investigative question "What are the favourite fruits of our class and their families?"
Gecko feet
In this unit of work we link the development of skip-counting patterns to bars on a relationship graph. We also plot our skip-counting patterns on a hundreds board.
In this unit we look at skip-counting patterns. These are patterns obtained by adding the same, constant, number to make the next number every time. So the difference between any two terms in a skip-counting pattern is the same. This is a good exercise to help reinforce the various concepts relating to pattern. In particular, it helps us to understand the idea of a recurrence relation between consecutive terms.
Skip-counting patterns are also called arithmetic progressions. In secondary school, expressions for both the general term of an arithmetic progression and the sum of all of the numbers in the progression are found.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate the tasks include:
The contexts for the skip patterns used in this unit can be adapted to suit the interests and experiences of your students. For example in the Exploring part of the unit:
Getting Started
Explain that today we will explore the pattern of 4s by counting the number of feet on geckos. We then use this information to build a relationship graph.
How did you work that out?
Share ideas. Encourage the students to focus on the relationship between the number of geckos and the number of feet.
Exploring
Over the next 2-3 days, the students work in pairs to explore the number patterns of other skip-counts. At the end of each session the students share their charts with the rest of the class.
Reflecting
In today’s session we use calculators to extend our skip-counting into the hundreds. We record our patterns on a hundreds chart.
Which number will be next?
How do you know?
Dear parents and whānau,
This week in maths we have been looking at skip-counting patterns and the charts that can be made from them.
Your child will be able to explain to you exactly what we did in class. Here is a chart made from a skip-counting pattern. Talk with your child about what the next number in the pattern will be. Put that number onto the chart. Discuss with your child how the pattern would continue.
Try to think of how that pattern might describe something in your whānau. Could you make a similar chart of another number pattern related to nature, sport, or another family interest.
This is an important part of maths. Thank you for your help.
Figure it Out Links
A link from the Figure It Out series which you may find useful is:
Link, Algebra, Book One, Which Wheels Where? Page 20.
Equality and equations
The purpose of this unit of five sessions is to develop the algebraic understanding that the equals symbol, = , indicates a relationship of equivalence between two amounts.
This sequence of lessons provides a fundamental and important foundation for students to be able to read, write, and understand an equation.
The essence of an equation is that it is a statement of a relationship between two amounts. This relationship is a significant one of equivalence. The understanding that the amounts on either side of the equals sign are equal in value, is essential if students are to experience success in algebra, and mathematics.
The most common misunderstanding is when students develop a process view of an equation as a procedure to follow to get an answer, rather than a structural or relational view of equivalence.
Students should be immersed in a range of experiences that support them to explore the concept of equivalence and balance. During these experiences, the teacher must carefully choose the language they use and model. As equations are introduced, recorded, read and interpreted, words and phrases such as ‘has the same value as’, ‘is the same as’, ‘is equal to’ and ‘ is equivalent to’, rather than ‘makes’, or ‘gives an answer of ’ become very important. It is interesting to note that the word ‘equals’, on its own, has subtly become more synonymous with ‘makes’ or ‘gives an answer’, rather than giving the message of equivalence that it should.
When posing problems that position the unknown amount at the beginning or in the middle of an equation, we challenge the students to explore the relationship statement and the operations from a different perspective. This also occurs when students are asked to find ‘different names’ for the same amount.
Students should have opportunities to read and respond to equations, and record them after having interpreted a number problem expressed in words. In developing the ‘balance’ view of an equation, students will understand the equality relationship expressed in an equation such as 6 = 6, rather than being perplexed by the fact that there is no number problem to ‘answer’. Students will also readily understand relationships expressed in equations such as 4 + 2 = 1 + 5, rather than developing an expectation that a single ‘answer’ will follow the = symbol. Instead of expressing solutions in the arithmetic ‘voice’ of ‘problem, calculation and answer’, it is important in early algebra work, for students to explain their solutions in words that make the equivalence relationship explicit.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate the tasks include:
The contexts used in the word problems in this unit can be adapted to suit the interests and experiences of your students. For example:
These learning experiences use numbers in the range from 1 to 20, however the numbers in the problems and the learning experiences should be adapted, as appropriate, for the students.
Session 1
SLOs:
Activity 1
Pose subtraction scenarios and have students record their number expressions.
For example:
Jack has eight beans and drops four. (8 - 4)
Jack has 6 beans and drops 1. (6 - 1)
Activity 2
Pose the problem:
“Jack wants to give away some packets of beans. He decides he’ll put six in each packet. He puts some beans of each colour into each packet and writes on the outside of the packet how many there are of each colour."
Write 6 on the class chart.
Demonstrate. For example:
Put 2 bright green and four dark green beans into one envelope and write 2 + 4 in pencil on the outside.
Tell the students that they should take turns to put the beans into the packets and to write on the outside.
6 is the same amount as:
Have students take turns to record their number expressions beside this.
6 is the same as: 5 + 1, 4 + 2, 3 + 3, 2 + 4, 1 + 5
Read these together using the language of, “is the same as.”
Ask whether it would be fair for Jack to give these to his friends. (Yes, because they would be getting the same amount. They would be getting an equal amount.)
Activity 3
Have students tell you what ‘equal’ means. Brainstorm ideas and record these.
6 is the same (amount) as: 5 + 1, 4 + 2, 3 + 3, 2 + 4, 1 + 5
6 is equal to: 5 + 1, 4 + 2, 3 + 3, 2 + 4, 1 + 5
Ask if students know how to write “is equal to” using a symbol. Introduce =.
Model writing 6 = 5 + 1.
Activity 4
Explain that Jack needs packets with these different amounts. Demonstrate, using a ‘six packet’, that each envelope must have the “number equals story” on it.
Activity 5
Conclude the session by reviewing =, equals and its meaning and the meaning of the word equation. Have students explain these, and record what they say.
Session 2
SLO:
Activity 1
Record a ‘six’ equation and read it in different ways together. For example:
6 = 5 + 1, “six is equal to five plus one”, “six is the same as five plus one”.
Highlight the fact that each of the packets in the 6 container have an equal or same amount.
Have students in pairs choose one of the containers (you may need to make multiples of each container depending on class size).
Students begin by taking turns to read aloud to their partner, in the two ways modeled in Step 1 (above), an equation on an envelope selected from the container. They should return these once read.
They should take two packets at a time, check that they have exactly the same amount and record what they find on their “stocktaking sheet” like this:
Students with containers 3 and 4 in particular, will accomplish this quickly.
Activity 2
Place in front of the students the cardboard ‘tickets’ and the plastic pegs.
Pose the task:
“Jack is going to have a bean stall. He needs ‘pegged pairs’ with ten beans altogether in each. We are going to help him. We need to make labels to show the contents, or what's inside."
Elicit from the students that by using one packet from each of their containers, they will have ten beans. If necessary, students can explore this idea and check, using their fingers, showing, for example: 10 = 7 fingers (up) and 3 fingers (down).
We say "7 beans plus 3 beans equals 10 beans" and we write 7 + 3 = 10
We say: "This envelope has 5 dark and 2 light (5 + 2) and this envelope has 1 dark and 2 light (1+2). Altogether that equals 10 so " We write: 5 + 2 + 1 + 2 = 10
Tip out the beans and write the number of each of the colours.
We say" There are 6 dark beans and 4 light beans and that is 10 beans altogether."
We write: 6 + 4 = 10
Review the words, equal, equation and the symbol =, recorded on the class chart in Step 1, highlighting the language of ‘is equal to’ and ‘is the same as’ and that all the equations written are different names for ten.
Session 3
SLOs:
Activity 1
Again, record and ‘test’ student ideas, trying different combinations of pegged pairs. For example:
5 + 5 = 6 + 4
6 + 4 = 7 + 3
Ask why the results are recorded using =.
Elicit reasons such as ,”equals shows that they are the same”, “equals shows that they balance”, “equals shows that both amounts have the same value (10)” , “equals means is the same as”.
Activity 2
Remove the packet of 4 beans, leaving 6 only on one side. Discuss the tipped scales and how to record the removal of the 4 beans.
Record suggestions. For example:
5 + 5 is not the same as 10 – 4
5 + 5 is not equal to 10 – 4
10 is not equal to 6
Accept, ‘put 4 back in again’, but work to elicit, ‘take 4 away from the other side.’
Have a student remove 4 beans from one of the 5 bean envelopes (example above), saying how many are remaining in the envelope (1). Return it to the scales.
Record suggestions that describe what has happened now the balance is restored. For example:
5 + 5 - 4 is equal to 10 – 4
10 - 4 is the same as 10 – 4
10 – 4 = 10 – 4
6 = 6
As equations are recorded, have students explain or demonstrate, using the materials, exactly what is happening. Together reach the conclusion: if you take away the same amount from each ‘side’ or pan, the scales will still balance.
Have student pairs combine the beans from the pegged pairs into single envelopes of ten beans, writing 10 on each.
Have students work in pairs with envelopes of ten beans, some spare beans, paper to record equations and a set of balance scales.
Have students undertake the following tasks
Student Two guesses how many were removed, removes this number from the other envelope, ‘secretly’ records the equation, for example 10 – 5 = 5, and returns it to the scales. They look carefully to check to see if the scales balance. If the scales do not balance, Student Two repeats their turn with another amount. When the scales do balance, both students share their final equations and check the amount in each envelope. Both students finally record the balance, for example, 7 = 7.
The students reverse rolls.
Student One places one ten envelope and a mixture of both colours of beans into one pan to make a number between ten and twenty. The student records the equation: for example, 10 + 2 + 3 = 15.
Student Two places one ten envelope and a mixture of both colours of beans into the other pan. The two-bean mix must be a different combination, but the total must balance the scales (in this case must equal 15). This student records their equation: for example, 10 + 1 + 4 = 15.
Both students then record what they can see in both pans.
10 + 2 + 3 = 10 + 1 + 4
15 = 15
It is important to highlight the balanced nature of the equations. Elicit from the students what their understanding is about equations.
Session 4
SLOs:
Activity 1
Explain that Jack, of Jack and the Beanstalk fame, has some problems for the students to solve and that they may want to use the equipment to help them.
Distribute a copy of Copymaster 1 to each student. Read through the problems together.
Highlight that each student will be writing equations for each problem.
Students should choose whether to work on the problems alone or with a partner; however, each student should complete their own recording sheet.
Session 5
SLOs:
Activity 1
Introduce the True/False game. (Copymaster 2)
(Purpose: To recognise when amounts are equal or not equal.)
Model a ‘true’ equation such as 1 + 3 = 2 + 2, highlighting the fact that the amounts on both sides are the same or equal to each other. Each expression is equal to 4. Model a ‘false’ equation such as 1 + 3 = 3 + 2, highlighting the fact that both sides are not the same and not equal to each other. 4 is not equal to 5. This is false (not true).
Students play in pairs. They shuffle the playing cards and deal 10 to each player. The remainder of cards is placed in a pile, face down, handy to both players.
The aim of the game is to be the first person to have an equal number of true and false equations (five of each).
As each player turns over their cards, they sort them into true and false groups, face up in front of themselves. If they have more of one group than the other, they continue to take cards from the top of the pile, till the number of their true and false cards is equal.
The first player to have equal numbers of true and false cards calls, “Stop!”
This caller must explain to their partner, for each of their decisions, how they know they are correct in their true/false decisions. They can use beans to support their explanation.
The game begins again. The winner is the person who wins the most of three games.
Activity 2
Students play Same Name snap, using cards from Copymaster 3.
Purpose: To recognise when amounts are equivalent (or not equivalent) and to give the ‘number name’ for the ‘same name’ expressions.
How to play:
Student pairs shuffle the cards and deal all cards so each student has an equal number of cards. These are placed in a pile, face down in front of each student. Student One turns over the top card and places it, face up, between both students. Student Two does the same, placing their card on top of their partner’s card. If the two expressions have equal value, either student calls Same Name, states the number that the expression represents, and the correct equation using either ‘is equal to’ or ‘is the same as’. For example:
2 + 3 is placed on top of 4 + 1.
“Same name! Five! Two plus three is equal to four plus one.” or
“Two plus three is the same as four plus one.”
The caller collects the card pile, records the equation, 5 = 2 + 3 = 4 + 1 on their scoring paper, and the game begins again, with the winner of this round placing the first card.
The student who does not call, can challenge the caller if they believe the “name” is not true for either or both expressions. If they are correct, they collect the pile and record the correct equation. The original caller must erase the incorrect equation.
The game finishes when one student has all the cards, or when one student has recorded ten ‘same name’ equations.
Activity 3
Conclude this session by discussing learning from the games, and reviewing ideas recorded on the class chart over five sessions.
Dear parents and whānau,
In maths this week the students have been learning how to read and write addition and subtraction equations. The algebra focus has been on helping the students to understand that equals (=) means “is equal to” or “has the same value as”, rather than being a sign that indicates “the answer”.
They have been playing the Same Name Game in class, so your child will be able to show you how to play. It would be helpful if you can use the phrases “is equal to” or “is the same as”, as you play the game together.
Thank you.
Making Patterns
In this unit students explore patterns involving transformations of shapes. Students make and identify patterns that involve translation, reflection, and rotation. They make their own patterns and pictures to show the transformations, and discuss with others how they included the different transformation elements.
Translations (slides), reflections (flips), and rotations (turns) are explored in this unit.
Translations are slides or shifts of a shape along a line.

Reflections are flips of a shape to make an image as though it is reflected in a mirror.
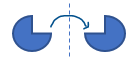
Rotations are turns, so when a shape is turned about a point, either inside or outside of itself, the image is a rotation of the original shape. This unit uses examples where the rotation happens around the centre point of a shape.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to make the tasks more accessible include:
The objects and pictures used in this unit can be changed to suit the interests and experiences of your students. For example, local flowers and pictures of native insects and butterflies are likely to be more engaging than generic pictures of flowers and butterflies. You could also incorporate an outdoor walk where students look for examples of translations, reflections and rotations. Images of Native plants, animals, butterflies and marine mammals can be found at: Doc Native Plants, Doc Native Animals, Native Butterflies Slideshow and Native Marine Mammals.
Te reo Māori vocabulary terms such as neke (translate), whakaata (reflect) and huri (rotate) could be introduced in this unit and used throughout other mathematical learning.
Session 1
In this session students make patterns that show translations.
Are the pictures the same each time? (Yes)
How are the pictures the same? (shape, size, orientation, colour)
Session 2
In this session students make patterns that show reflections.
Session 3
In this session students make patterns that show rotations.
Sessions 4 and 5
In these sessions students make an underwater sea picture that shows translation, reflection and rotation.
Which animal shows reflection? (Octopus)
How else could you show reflection in your picture? (Put two fish nose to nose.)
How could you show the translation in your picture? (Use 2 or more of the same animal and orientate them the same way.)
How could you show rotation in your picture? (Use 2 or more sea stars and rotate each one.)
Dear parents and whānau,
This week we have been making patterns. Your child is going to be a Pattern Detective and look for patterns at home and in their neighbourhood that show translations (a picture or pattern that repeats to make a pattern) or rotations ( a picture or pattern that repeats around in a circle). One place to look for these is in wallpaper or tiling. These patterns can also be found in nature. Please ask them to explain what is happening in the patterns they find.
Matariki - Level 1
This unit consists of mathematical learning, at Level 1 of the New Zealand Curriculum, focused around celebrations of Matariki, the Māori New Year. The sessions provide meaningful contexts that highlight Māori culture and provide powerful learning opportunities that connect different strands of mathematics.
In this unit the students will apply different mathematical and statistical ideas, such as the properties of symmetry. In this, they will demonstrate understanding of the features of a shape that change and remain invariant under translation, reflection and rotation.
Students also apply simple probability. For example, given this set of cards, what is the chance of getting a bright star if you choose one card at random? Random means that each card has the same chance of selection.
The set of all possible outcomes contains four possibilities. Two of those possible outcomes are selecting a bright star card. The chances of getting a bright star are two out of four or one half. There is a one quarter chance of getting a fuzzy star and the same chance of getting a rainy cloud.
The learning opportunities in this unit can be differentiated by providing or removing support to students, or by varying the task requirements. Ways to support students include:
Although the context of Matariki should be engaging, and relevant, for the majority of your learners, it may be appropriate to frame the learning in these sessions around another significant time of year (e.g. Chinese New Year, Samoan language week). This context offers opportunities to make links between home and school. Consider asking family and community members to help with the different lessons. For example, members of your local marae may be able to share local stories and traditions of Matariki with your class.
Te reo Māori language is embedded throughout this unit. Relevant mathematical vocabulary that could be introduced in this unit and used throughout other learning include āhua (shape), shape names (e.g. whetū - star), hangarite (symmetry, symmetrical), whakaata (reflect, reflection), huri (rotate, rotation), tātai (calculate, calculation), tāpiri (add, addition), hautau (fraction), raupapa (sequence, order), tūponotanga (chance, probability), and ine (measure).
Lesson One
What shape is a star?
Today we are going to make some stars to display using shapes.
How do you know that you have got all the diagonals? (Students might notice that the same number of diagonals come from each corner)
Does the star have mirror lines? How do you know?
Lesson Two
In this lesson your students explore family trees, working out the number of people in their direct whakapapa. This may be a sensitive topic for some students. Thinking about our relatives who are no longer with us, or have just arrived, is a traditional part of Matariki, the Māori New Year. According to legend, Matariki is the time when Taramainuku, captain of Te Waka O Rangi, and gatherer of souls, releases the souls of the departed from the great net. The souls ascend into the sky to become stars.
That question needs to be treated sensitively but the focus is on biological parents, usually a father and mother. You might personalise the answer by telling your students the names of your mother and father. Draw a diagram like this, or use an online tool to create the diagram:
My mother and father had parents too. What are your parents' parents called?
How many grandparents (koroua) do you have?
Students may have different ways to establish the number of grandparents, such as just knowing, visualising the tree and counting in ones, or doubling (double two),
Nowadays, many students will still have living great grandparents. You might personalise the idea using your whakapapa.
What do we call the parents of your great grandparents?
Now I want you to solve this problem. How many great great grandparents do you have?
Use the context as a vehicle for introducing even numbers (multiples of two), Act out three children getting their parents (other students) and bringing them to school. Change the number of students and work out the total number of parents. Find a way to highlight the numbers that come up, such as shading the numbers on a virtual Hundreds Board.
Students might notice that even numbers occur in the 0, 2, 4, 6, 8 columns of the hundreds board.
Lesson Three
Matariki is a time for cultural activities, such as story-telling, music, and games. Titi Rakau is a traditional game that involves hitting and throwing sticks, usually to a rhythmic chant. It was used to enhance the hand-eye coordination of children and warriors. Rakau can be used as a vehicle for fractions and musical notation, as well as physical coordination. You can make the tasks below as simple or as difficult as you like.
What fractions has the bar been broken into? (Quarters)
Each of these notes (crotchet) is one quarter of a bar in this music.
The popular chant associated with Ti Rākau (E Papa Waiari - available on YouTube) is in 6/8 time meaning there are six quaver beats to a bar. If you watch a video of a performance with Rākau the sticks are often hit on the ground on the first and fourth beats, or clicked together on the second, third, fifth and sixth beats.
Lesson Four
The rising of Matariki, in late May or June, signals to Māori that it is the start of a new year. It is appropriate for students to reflect on the passage of time. For young students there are important landmarks in the development of time, including:
Cooking in a hāngī
In the first part of the lesson students work with the first two ideas, recalling the past and anticipating the future.
Watch carefully. At the end of the video I will ask you about how to make a hāngī.
I want you to put the pictures in the order that they happened. Put them in a line. Be ready to explain why you put the pictures in that order.
Why does this happen before this?
Why does this happen after this?
What might have happened before the hole was dug?
What might have happened after the food was served?
Chances of a good year
In former times, tohunga, wise people of the village, looked at the sky before dawn to watch the rising of Matariki. They used the clarity of the stars to predict what the new year would bring. A clear sky with the stars of Matariki shining brightly signalled a good season for weather and the growing and harvesting of crops. A cloudy sky signalled bad luck.
If you saw this, what would you predict?
There will be plenty of rain but not too much, and the crops will grow well.
It is going to be a bit windy.
There will be lots of food in the rivers, lakes and sea.
Lesson Five
This lesson involves making rēwena paraoa (potato bread). The process of making it takes three stages; preparing the ‘bug’, mixing and baking, then serving. Therefore, it is not a continuous lesson. Preparation and serving food are important activities for Matariki celebrations. It would be beneficial to invite older students, or community members, in to help with this session.
2 cups of flour
1 teaspoon of sugar
Up to one cup of luke-warm water (as needed to maintain a paste-like consistency)
How many slices should we make?
How thick will the slices be?
How many cuts will we make?
Dear family and whānau,
This week we have been exploring shapes and sequencing events. Ask your child to find examples of shapes such as triangle, square, hexagon and trapezium around the house. Ask them about how the shapes were used to make stars in class. To extend the work we have been doing on sequencing events, when you are engaging in activities at home that have a defined sequence, ask your child questions to explore before and after actions, for example why does this happen before this? What might happen after we have done this?
Arty Shapes
In this unit ākonga participate in a variety of art based activities to develop their knowledge of 2-dimensional shapes. They use their own language to describe their works and the shapes they have used.
This unit begins an exploration of basic 2D shapes, their properties and the mathematical language associated with them in both te reo Māori and Engligh. There is a progression from the way the ākonga think of and see these objects to the more formal mathematical ideas and descriptions. In order to be able to communicate on any topic, there is a need for a common language. This unit takes the initial steps in the formulation of this common language.
The learning opportunities in this unit can be differentiated by providing or removing support to ākonga and by varying the task requirements. Ways to differentiate the tasks include:
The context for this unit can be adapted to suit the interests, experiences and cultural makeup of your ākonga. This unit begins with looking at Piet Mondrians's artwork. In Session One, ākonga practice identifying shapes and describing them. Instead, or following this discussion, you could work with ākonga to identify art in their culture. Possible contexts of art in te ao Māori could be raranga/weaving, whakairo/carving, or peitatanga/painting. The art that is utilised in this learning should make clear links to the specific learning outcomes, meaning it should include images of 2-dimensional shapes (i.e. triangle, square, oblong, circle, oval, diamond).
Te reo Māori vocabulary terms such as tahi (one), rua (two), toru (three), tapatoru (triangle), tapawhā rite (square), tapawhā hāngai (non-square triangle), porowhita (circle), porohema (oval) and taimana (diamond) could be introduced in this unit and used throughout other mathematical learning.
Throughout each session encourage the ākonga to talk about what they are making and the features of the shapes they are using. Discuss the similarities and differences in shapes and encourage a wide use of a range of terms. Counting the numbers of sides and the numbers of corners each shape has is also a good way to get ākonga to focus on shapes.
Questions or pātai to use:
A word wall, vocabulary poster, or T chart may be a useful scaffold for ākonga to use throughout this unit.
Session 1: Shape collage
Begin the session by looking at some of Piet Mondrian’s primary coloured and cubist art works. Have ākonga identify the shapes they can see and describe these.
As the ākonga identify the shapes and their features, record these in a visible place (e.g. whiteboard, on a large poster).
Session 2: String shapes with PVA
Session 3: Shape stencils in crayon and dye
Session 4: Shape mobiles
Session 5
In this session ākonga reflect on one of their art-works made in the previous sessions, discuss and describe it and write about their work. Encourage ākonga to use both te reo Māori and English to describe their artworks.
Their writing could then be published and displayed, either in a classroom display or in a large book for the book corner. Encourage ākonga to share their produced artwork and learning with family and whānau.
Family and whānau,
This week at school we are looking at different shapes and the ways they are used in art works. It would be great if you could walk around your home and discuss the pictures on the walls with your child. Encourage them to tell you about the shapes they see.
Teen numbers (building with ten)
The purpose of this unit of sequenced lessons is to develop knowledge and understanding of the place value structure of numbers from ten to twenty.
When ākonga meet the number ten they meet a two-digit number for the first time. They begin to develop awareness of the concept that there are no more numerals to learn and we just ‘recycle’ them. This is their entry into the structural world of our tens based number system.
Ākonga are introduced to the language of digits, place and value. It is a considerable conceptual shift for ākonga to move from a face value understanding (i.e. that a numeral represents a number of units that can be counted) to a complex place value understanding in which a numeral can represent a group or a number of groups, that are in themselves made up of units that can be counted.
As ākonga study teen numbers and their meaning and structure (rather than simply ‘saying’ them in a counting sequence), the focus is on developing the understanding that the value of a digit depends on its' place. This is not trivial and it is made more challenging by the language of teen numbers.
Ākonga often confuse the number names such as ‘fourteen’ and ‘forty’ because the adult enunciation of the word endings is often unclear. In hearing ‘fourteen’ ākonga may expect to see the 4 appear first in the symbolic form because that is the number that comes first when they say it. Seeing 14 and hearing ‘four – teen’ therefore has the potential for confusion.
Ākonga need many opportunities to make these numbers with materials. When using place value material for the first time, ākonga need the opportunity to group single units to make one ten. By doing this they come to understand that ten ‘ones’ or units do in fact comprise one 'ten'. The first equipment to use therefore is that which can be physically grouped, one by one, to make or compose one group of ten, or a ‘ten’, and be able to be unpacked or decomposed again into ten ones. When this is complemented by symbolic recording that accurately matches the representation of the number, understanding of two-digit notation is developed. Equipment in which the tens are already pre-grouped can be used once grouping to make ten is well understood.
It is a considerable shift for ākonga to then use materials in which the ten looks completely different from the ones (for example, money) and to trust the 'ten for one' trade. The greatest abstraction is the digits in our number system, where the tens and ones look exactly the same but it is only their place that tells their value.
In depth exploration of place value with teen numbers is essential if our ākonga are to work with real understanding of the numbers within our number system.
The activities suggested in this series of lessons can form the basis of independent practice tasks.
The learning opportunities in this unit can be differentiated by providing or removing support to ākonga and by varying the task requirements. Ways to differentiate the tasks include:
Using the place value language structure within te reo Māori to develop and reinforce the understanding that teen numbers represent 'ten and' may support conceptual understanding of teen numbers. Display a chart to reinforce this conceptualisation. Oral communication of te reo Māori for numbers up to 20 will also be useful in the context of enhancing the interest and cultural relevancy of this learning.
Session 1
SLOs:
Activity 1
Repeat with several teen numbers.
Activity 2
Have ākonga work in pairs to play Teen Pairs. Consider pairing together ākonga of mixed mathematical abilities to encourage tuakana/teina.
Purpose: to recognise and match teen number representations and the words ‘ ten and ____’
Ākonga place between them two piles of cards face down (Copymaster 1).
Pile 1: Tens frame teen number cards (showing two tens frames).
Pile 2: Word Ten and _____ cards.
Ākonga take turns to turn over one tens frame teen number card and say the number of dots they see. They then turn over a word card and read the words aloud. If the tens frames and word card match, they keep the matching pair. The winner is the ākonga with the most pairs.
For example:


Activity 3
12 is ten and two
Session 2
SLOs:
Activity 1
Hold up the ten bundle and ask, 'Do I still have ten sticks here?' (yes) 'How many bundles of ten do I have?' (1). Record this on the chart, for example, I have fifteen. 15 is ten and five. 15 is 1 ten and 5 ones. Discuss the language of ‘ones’ and that sometimes ‘ones’ can be called ‘units’.
Activity 2
If available, have ākonga work in small groups or pairs to explore, find and display the four matching cards in the BSM 9-1-48 card game.
Alternatively, ākonga can make a class puzzle matching game. Provide each ākonga with card, pens and scissors. Have them make their own puzzle pieces which can then be combined with those made by their classmates and mixed up to make a matching pairs game. Before cutting these up, photocopy an extra 3 or 4 sets to be used later on in this unit.

Activity 3
Ākonga deal out 7 cards each. The remaining pile of cards is placed in the centre of the group. Ākonga take turns to ask one other player for a card needed to complete a set of 3 teen family cards. If the other player does not have the card sought, the requesting player takes one from the pile. As sets are complete, ākonga place these in front of them.
The winner is the player with the most complete sets.
Session 3
SLOs:
Activity 1
NB. The container for the beans looks different from the ones, but can still be unpacked. This is a subtle and important shift. Also consider exploring together as a group or class the place value beans animation, available from https://e-ako.nzmaths.co.nz/modules/PVanimations/
Activity 2
Ākonga play Go Teen in pairs. A tuakana/teina model could work well here.
Purpose: to use ten ones to make one group of ten, when adding two single-digit numbers.
Ākonga have playing cards (ace - 9), shuffled and face down between them. Alternatively you could print out numeral cards 1-9. They have single beans and empty tens containers (or single ice block sticks and hair ties), single digit and tens arrow cards available.
The players take turns to turn over two playing cards. When the two numbers are added, if they make less than ten they return them face down to a discard pile.
If they make more than ten they keep their playing cards, take the total number of beans, group the materials showing the total as 1 ten and units. They also show the number with the arrow cards.
However, if the number has already been made by their partner, (the arrow cards for that number have been used) the ākonga must simply return their playing cards to the discard pile.
The winner is the player with the most tens (containers with beans) when all the arrow cards have been used up.
Session 4
SLOs:
Activity 1
A problem is posed in which the number being subtracted requires the ten to be ‘unpacked’ or decomposed:
'Here are the beans Gardener Gavin is going to plant. He plants 9 in the first row. How many beans are left to plant in the second row? How can we work this out?'
Ākonga can discuss strategies for subtracting 9 and suggest what they can do with the materials. Kaiako models this and some more examples can be explored together.
Activity 2
Purpose: to understand how to compose and decompose a ten.
Equipment: Ākonga beans and containers, numeral cards 11- 14, a set of playing cards 2 – 5, a dice with a + or – symbol marked on each of the six faces, mini whiteboards and markers.
How to play:
For example: one ākonga turns over and models 13, rolls + and 3, and makes 16.
At their next turn the ākonga may have to – 4, followed on the next turn by – 3.
This will require the ākonga to decompose the ten.
The ākonga will have recorded for the three turns so far:
13 + 3 = 16
16 – 4 = 12
12 – 3 = 9
Conclude the lesson with a focus on the words, ‘place value’. The kaiako writes ‘place value’ on a chart and asks ākonga what this could mean. They are encouraged to look at all the recording of teen numbers completed throughout these lessons. Accept all responses, but conclude by highlighting and recording that 'the place of a numeral in a number tells us what it is worth or its value.' Show the enlarged arrow cards drawing attention to the words tens and ones.


Dear parents and whānau,
In maths this week we have been learning about teen numbers and how they are made of ten plus a single digit number. For example, thirteen is 10 + 3. We have also been introduced to place value, learning that the 1 in 13 is in fact one group of ten.
You can help your child practice this very important idea by playing the game, Teenager match.
Cut up the attached page to make separate cards. Spread them face down on the table. Take turns to choose a pair of cards. If they match, keep the pair. The winner is the person with the most pairs.
[Include a copy of Copymaster 5]
Seesaws
This unit involves the students directly comparing the weight (mass) of two or more objects.
Weight is a measure of the force of gravity on an object. Mass is the amount of matter in an object and a measure of the force needed to accelerate it. This means that the mass of the object on the moon is the same as its mass on earth, but its weight is lighter on the moon. In a science context, weight is measured in Newtons (N), and mass is measured in kilograms (kg), grams (g), and milligrams (mg). However, these terms are often used interchangeably. For practical purposes, the language commonly used to measure weight and mass in everyday life is kilograms, and grams. Choose one term (e.g.weight or mass) and use it consistently with your students.
An important early goal in measurement is for students to understand the attribute they are going to measure. Comparison activities help students develop an understanding of the attribute that is being measured. In the case of mass, the most personal experience is comparing the weights of two objects by holding one in each hand and feeling which has the greatest downward pull. This personal experience can then be transferred to the use of balance and spring scales.
Young students are influenced by what they see. The shape or the size of an object can easily deceive them. For example, students who do not yet conserve the property of mass will think that if the shape of an object changes then so does its mass. In one of the stations, in this unit, the students change the shape of a piece of plasticine and then weigh it to see that the weight has stayed the same.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to provide more support include:
Te reo Māori vocabulary terms such as taimāmā (light), taumaha (heavy), ine-taumaha (scale for measuring weight) and maihea (weight) could be introduced in this unit and used throughout other mathematical learning.
The objects weighed in this unit can be selected to suit the interests, experiences and culture of your students. For example, the students could bring small objects from home or objects that they can collect from around the school playground (e.g. stones, cones, twigs or shells). Bringing items from home might offer important opportunities for oral language (i.e. sharing) When students are making objects out of plasticine, students could make objects to reflect their current learning interests (e.g. a snail, if you are learning about minibeasts). Consider how the use of different objects might reinforce learning from other areas, and contribute to a cohesive learning experience across all sessions/stations.
Station One: See-saws
In this station we work with a partner to make a see-saw using a soft-drink can and a shoe box lid. We then use the see-saw to find objects that are the same weight.
Stop the soft drink can from rolling by fixing it to the table with tape or by putting plasticine rolls on each side.
How did you make your see-saw?
What are some things you found that balance? Show me.
Have you ever been on a see-saw? What happens?
Station Two: Weighing balls and worms
In this station the students, in pairs, experiment with plasticine or play dough to find that changes in an object’s shape does not change its weight.
Will your kiwis be the same weight? Why /Why not?
Check on the balance scales.
Whose worm is longest?
Whose worm is heaviest? Check?
Why are they the same weight?
Whose has made the most balls?
Which ball is the heaviest? Check?
If you both put all your balls together on the seesaw what do you think will happen?
What do you notice? Why is the seesaw balanced?
Station Three: What balances Freddy Frog?
In this station the students experiment to find items that balance Freddy Frog (or an alternative object eg Terry Tui). The students paste their solutions onto a class chart.
What happens on the scales when Freddy is heavier?
Do you think that this "car" will be lighter or heavier? Why do you think that? Were you right?
What are some of the things that you found that were the same weight as Freddy Frog?
Station Four
In this station we line objects up in order of weight so that we can work out who goes where in our "tower". We need to have the heaviest at the bottom and the lightest at the top. Note this activity can also be taken outside using natural materials.
Were your guesses correct?
Tell me how you put the toys in order?
Did you find a lighter toy on your first guess?
How did you check your guess?
Station Five: Bungees
In this station students use a simple piece of elastic as a bungee and measure how far the elastic stretches to compare the weight of different objects.
Dear family and whānau,
This week we have been comparing the weight of objects using soft drink "see-saws" and bungee strings. We have been encouraging the children to use words such as heavier and lighter to compare the weight of objects. Do you speak a language that is not English at home? Perhaps you could discuss these terms at home, and write them down for your child to share with us at school.
At home you might like to make your own "see-saw" or bungee and then use it to compare the weights of small objects.
1. Make a see-saw using a soft-drink can, a shoe box lid and some tape.
2. Make a bungee by attaching a clip to a thin elastic, which is suspended from string.
Skip it to multiply it
This unit explores early multiplication where ākonga are encouraged to skip count to solve story problems, rather than counting all.
This unit develops the skill of skip counting to find the total of several equal sets. At Level One, ākonga are expected to use a range of counting strategies such as counting on, counting back and skip counting. Both conceptual understanding and procedural fluency are important to counting. Skip counting involves understanding that a set can be treated as a composite unit. The last number counted tells how many objects are in the set. Composites can be combined whether they are equal or not, but skip counting (e.g. 5, 10, 15, 20) can be used particularly when the sets are equal. The procedural fluency ākonga need to enact skip counting is knowledge of the skip counting sequences. Ideally, learning word and numeral sequences, like 2, 4, 6, 8… are learned in conjunction with quantity. That way, ākonga realise that the next number is the result of adding two more objects to what is already there.
As well as knowing skip counting sequences, ākonga need fluency in tracking the number of counts. Initially they may use fingers to do that. For example, the fingers in four hands might be skip-counted as 5, 10, 15, 20, while the number of hands is tracked as 1, 2, 3, 4.
The learning opportunities in this unit can be differentiated by providing or removing support to ākonga and by varying the task requirements. Ways to differentiate the tasks include:
The contexts for skip patterns used in this unit can be adapted to suit the interests and experiences of your ākonga. For example:
Te reo Māori vocabulary terms such as tatau māwhiti-rua (skip count in twos), tatau mawhiti-rima (skip count in fives), whakamua (forwards), and whakamuri (backwards) could be introduced in this unit and used throughout other mathematical learning.
Each of the following sessions is designed to take 20 to 25 minutes. This series of sessions can be used in whole class (mahi tahi) or small group situations. The first session develops ākonga ability to skip count in a variety of ways.
Session 1 – Skip Counting
Encourage ākonga to continue counting while you record the numbers they are saying in a loud voice on the board. Then stop and talk about the number sequence and the patterns they can see.
What can you tell me about the big voice numbers?
What patterns can you see?
What patterns did you see?
What numbers are missing from the pattern?
Session 2 – TūĪ in Kōwhai trees
Here are four kōwhai trees.
Place two tūī in (under) each kōwhai tree.
There are two tūī in each kōwhai tree (uncovering the collections and hiding them sequentially). How many tūī are there altogether?
Try to record their responses e.g. Len thought 1, 2, 3, 4, 5, 6, 7, 8; Elinda went 1 2, 3 4, 5 6, 7 8; Hemi went 2, 4, 6, 8; and Kelly went 4 + 4 = 8 (note that this is an additive, not counting, response).
For example, “There are 6 kōwhai trees on High Street. There are 5 tūī in each kōwhai tree. How many tūī are there altogether?” Encourage ākonga to explain how they got their answer.
Session 3 – Fish in Fishponds
How many fish are there altogether?
How can we work it out without counting the fish one by one?
Did anyone do it a different way?
Is there a quick way to work out how many fish there are left?
Session 4 – Cartons and Eggs
How many eggs are there altogether? (You might have cubes, ping pong balls, or other objects as the make-believe eggs).
Sixes are hard to count with, so we are going to use smaller cartons today.
I want you to make problems for each other using the same sized cartons.
You can record your strategies using numbers.
Be ready to share one of your problems with the whole class at the end.
Session 5: Legs on animals
How many legs would be on five goldfish? Do ākonga still realise the problem can be written and solved, 5 x 0 = 0?
How many legs would be on 10, 50, 100 goldfish?” What is always true?
How many legs would be on 10, 50, 100 1-legged kiwi? What is always true?
Dear family and whānau,
At school this week we have been using skip counting to solve simple multiplication problems. At home this week we would like your child to practice skip counting forwards and backwards in twos and fives. Try doing this with them by clapping a beat together or by following a number strip. Change the starting numbers for the sequences.
Start from 2:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …
Count down from 14:
4, 12, 10, 8, 6, 4, 2.
Start from 5:
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …
Start from 15:
15, 20, 25, 30, 40, 45, 50, …
Count down from 45:
45, 40, 35, 30, 25, 20, 15, 10, 5.
Snakes and Scarves
In this unit we explore linear patterns using snakes as the context. We examine, construct and record snakes of different patterns. We also put scarves on our snakes and predict what is hidden.
The main idea behind this unit is for ākonga to develop basic concepts relating to pattern by exploring simple patterns in a novel situation. Ākonga will use multi-link cubes masquerading as snakes. The snakes have colourful ‘skin’ (it's a good chance for everyone to use their imagination). Ākonga play with a variety of snakes, both inventing their own and investigating ones made by other ākonga. In the process, they should begin to see that:
(i) patterns are made up of repeating sections of coloured cubes;
(ii) they can continue a pattern by adding on more cubes of the right colours; and
(ii) they can predict parts of a pattern that are missing.
Pattern is an important idea both in mathematics generally, and as a precursor to algebra. Discovering patterns enables us to predict events. For example, by knowing how the tides work we can predict when high tide will be and when will be a good time to go fishing. This pattern concept generalises in secondary school to finding results that work again and again.
The learning opportunities in this unit can be differentiated by providing or removing support to ākonga and by varying the task requirements. Ways to differentiate the tasks include:
The snake context used in this unit could be adapted to other animals such as huhu grubs, worms or eels. Alternatively, ākonga could come up with their own creature that has a multi-coloured, pattern body.
Te reo Māori vocabulary terms such as tauira (pattern) and He aha muri? (What is next?) could be introduced in this unit and used throughout other mathematical learning. Also, the simple counts and primary colours used in the unit provide an opportunity to use te reo Māori and Pasifika words alongside English, for example, whero (red) and tahi (one).
Getting Started
Today we investigate snakes with special colour patterns. We think about what would come next as we increase the length of our snakes. We also think about what happens when we cover part of our snake with a scarf.
Share ideas about patterns. Encourage ākonga to look around the classroom or think about places in their community for examples of patterns. For example, kōwhaihai patterns at marae or flower patterns at community gardens.
[Make a snake with a blue, red, blue, red, blue pattern.]
Who knows what colour comes next in our snake?
How did you know?
Who knows what colour comes next?
How did you know?
What cubes are hidden?
How did you know?
Exploring
Over the next 2-3 days we examine, construct and record the patterns of our snakes. We cover parts of our snakes with scarves and play ‘guessing games’ with other ākonga.
Can you tell me about your snake?
What colour cubes is your snake made of?
Can you see a pattern in your snake?
With all the ākonga gathered together (mahi tahi model) ask:
What cubes do you think are hidden under the scarf?
How do you know?
Reflecting
We conclude the unit by sharing the pattern snakes that we have made. We look for snakes that are alike.
Dear parents and whānau,
This week in maths we have explored repeating patterns using snakes made of different coloured cubes. We have practised predicting what cubes are hidden when the snake puts on a scarf.
Ask your child to tell you about the pattern of this snake and how the pattern could be continued.
Which cubes do you think are hidden under this scarf?
Can you and your child find or make some simple repeating patterns like this around your home? You could talk about them and play a game covering parts of them and saying what is hidden. For example, items of clothing, mugs, toys, rugs or duvets.
Lonely kiwi
In this unit we have a first look at uncertainty and chance. We begin to develop an intuitive sense of what chance and possibilities are about through games that involve following rules, making predictions and seeing what happens.
Although students at this level won't be ready to fully grasp the idea of chance they will develop some valuable intuitive notions. Underlying the activities is the idea that some events can be influenced by information, whereas others rely largely on luck. This provides the basis for the two ways of determining probabilities: theoretically and experimentally. Later on, we explore certain situations such as rolling dice, using spinners, choosing cards to determine precise values of probability. This is the theoretical aspect. Ideally you would always like to do this as you are then sure exactly what the probability is. However, in other situations we have to rely on a series of experiments and deduce the likely probability of an event through the long-term frequency of its occurrence. This applies to the kind of events that insurance companies are interested in such as the likelihood of an accident or the length of life of a 30 year old male.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to adjust the difficulty of the tasks include:
The contexts for this unit can be adapted to suit the interests and experiences of your students. For example:
Te reo Māori vocabulary terms such as ika (fish), ōrite (same), rerekē (different) and tūponotanga (chance) as well as colours in te reo Māori (such as whero, ma, kōwhai, etc) and counting from tahi ki tekau (one to 10) could be introduced in this unit and used throughout other mathematical learning.
Session One: Tūi and Kereru
In this first session we make our own set of cards using pictures of Tūi and Kereru.
Shuffle the cards.
Put the cards face down in one pile.
Players decide who will collect "same pairs" and who will collect "different" pairs.
Take turns turning a card from the top of the pile.
Compare the two cards. If they are the same, the player collecting "same pairs" takes them. If they are different, the other player takes them.
The game continues until all cards are used.
The winner is the player who collects the most cards.
Was one of the players luckier than the other one? What made you think this?
How many times did you win?
How many times did your partner win?
Was it better to be a "same" or a "different"? Why?
(note: The probability of different pairs is slightly greater than that of same pairs.)
Session Two: Tūi, Kereru and Kea
I this session we add 6 Kea to our pack of Tūi and Kereru cards and play the game again.
Was one of the players luckier than the other one? What made you think this?
How many times did you win?
How many times did your partner win?
Was it better to be a "same" or a "different"? Why?
Was it easier to win today? Why/Why not?
Session Three: The little lost kiwi
In this session we add one kiwi to our pack of Tūi, Kereru and Kea and play a new game.
Rules:
Spread the cards out face down.
Players take turns to turn over two cards.
If the cards are the same the player keeps the pair of cards but does not have another turn.
If the cards are different the cards are turned back face down.
Continue taking turns until all the cards (except the kiwi) are collected.
What card do you think you will turn up next? Why do you think that?
Which cards do you think will be the last?
Which are the hardest pairs to find? Why?
Which are the easiest pairs to find?
What can you tell me about the kiwi?
Why do you think the game is called The little lost kiwi?
Can you think of another name for our game?
Session Four: Greedy Pūkeko
In this activity the students roll a dice to feed fish to our three Pūkeko. The students will investigate the chance of giving a fish to their Pūkeko.
Rules:
The students take turns rolling the dice.
The student whose colour shows gives their Pūkeko a fish.
The game continues with players taking turns until all the fish are eaten.
Which coloured Pūkeko got the most fish?
Was there a lucky colour in your group?
Was it lucky in all the groups? Why/Why not?
Session Five: Feeding Greedy Pūkeko
In this game the students experiment with different dice.
Rules:
The students take turns first selecting and then rolling one of the dice.
They give a fish to the Pūkeko whose colour is shown.
The game continues with players taking turns until all the fish are eaten.
Which Pūkeko got the most fish?
Was there a lucky colour in your group? Why?
Was it lucky in all the groups? Why/Why not?
What difference did the dice you chose make?
In the game we want to stop Greedy Pūkeko from screeching for food. What should we do? (Check that the students understand that they need to feed Greedy Pūkeko to stop him screeching.)
Dear parents and whānau,
This week we have been learning about probability by playing games. As we have played the games we have thought about how likely it is to get certain things. Your child will bring home one of our copies of Little Lost Kiwi. As you play the game you could help your child by asking questions that focus on the likelihood or chance of finding pairs. What card do you think you will turn up next? Why do you think that? Which cards do you think will be last? Which are the hardest pairs to find? Why? Which are the easiest pairs to find? What can you tell me about the pig? Why do you think the game is called The little lost kiwi? Can you think of another name for our game?
Rules for Little Lost Kiwi.
We hope that together you enjoy playing Little Lost Kiwi.
The teddy bears’ fraction picnic
This unit supports students to equally partition objects and sets into fractional parts.
In this unit students explore equal partitioning of objects and sets, and how to name the parts they create using fractions. The easiest partitions are those related to halving since symmetry can be used. For example: halves come from partitioning a whole into two equal parts, and quarters come from partitioning a whole into four equal parts.
An object is partitioned according to an attribute, or characteristic. For example, a banana might be partitioned by length, but a sandwich partitioned by area. Some attributes are more difficult to work with than others. Length is the easiest attribute but others such as area, volume (capacity), and time are more difficult.
The results of partitioning a set into fraction parts can be anticipated, using number knowledge and strategies. For example, one quarter of 20 could be found by:
In this unit we apply three criteria when evaluating students’ capacity to partition and object or set into fractional parts:
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. The difficulty of tasks can be varied in many ways including:
The contexts for this unit can be adapted to suit the interests and experiences of your students. For example:
Te reo Māori vocabulary terms such as hautau (fraction), ōrite (equal), haurua (half), hauwha (quarter), hautoru (third) and toha (share) as well as counting from kore ki tekau (zero to 10) could be introduced in this unit and used throughout other mathematical learning. Other te reo Maori that could be useful in this unit are teti pea (teddy bear) and hanawiti (sandwich).
Session One
Rawiri and Hine are friends. They always share their food equally. How could they cut this sandwich? (Slide Two)
What does equal mean?
What do we call these pieces? (halves)
Why do you think there is a 1 and a 2? (2 refers to the number of those parts that make one)
Is the sandwich cut in half? Why? Why not?
What other ways could Rawiri and Hine cut their sandwich in half?
Cut this sandwich in two pieces that are not halves.
What is true for the sandwiches that are cut in half?
What is the same or the sandwiches that are not cut in half?
The key idea of halving is that both Rawiri and Hine get the same amount of sandwich. As the sandwich is not exactly symmetric through a horizontal mirror line you might get interesting conversation about the equality of shares. Slide Five may provide some stimulus for the discussion. Using the cut-out pieces of sandwich, show how halves map onto each other by reflection (flipping) or rotating (turning). With paper sandwiches you can fold to show that mapping of one half onto another.
Can your students distinguish when a shape or set has been halved?
Session Two
In this session, students explore the impact of other Teddy Bears joining in the picnic. What happens to the size of the portions as more shares are needed? How do we name the shares?
Imagine that four Teddy Bears went on the picnic instead of two. Pāpā still packed the same amount of food. What would happen then?
How could we cut a sandwich into four equal parts? What will the parts be called?
Does each Teddy Bear get the same amount of sandwich?
Common solutions are:
Students often miss the option of dividing the area of the sandwich by length…
Or other possibilities…
This time the challenge is to share each picnic food into quarters.
The shape of the sector of cheese places a restriction on how it can be partitioned. Likely responses are (left is correct, right is not):
Finish the session with the game called ‘Make a whole sandwich.” Students need copies of the first page of Copymaster 3 (halves and quarters) and a blank dice labelled, 1/2, 1/2, 14, 2/4, 3/4 and choose. The aim of the game is for players to make as many whole sandwiches as they can.
Players take turns to:
At any time a player can rearrange their sandwich pieces to make as many whole sandwiches as possible. Time the game to finish in five minutes which is long enough to gather a lot of pieces.
Session Three
In this session, students explore the equal sharing of picnic foods among three Teddy Bears. Thirding an object or set is generally harder than quartering because symmetry is harder to use. Your students should observe that thirds of the same object or set are smaller than halves but larger than quarters.
We explored how to cut sandwiches into two and four equal parts. What are those parts called? (halves and quarters)
What parts will we get if we share the food among three Teddy Bears?
Which is bigger, one half or one quarter? Why?
How big do you think one third will be? Why?
Find different ways to share one sandwich equally among the three Teddy Bears.
Is this sandwich cut into thirds? (No, the parts are unequal)
Do the parts have to be the same shape to be equal? (Banana is a good example)
Why are thirds harder to make than halves and quarters? What other fractions would be hard to make? Why?
PowerPoint 2- Slides 9-11, show how halving quarters produces eighths and halving thirds produces sixths. It is important for students to connect the naming of these equal parts to how many of those parts form one whole (sandwich).
One sixth Two sixths Three sixths Four sixths
(or one third) (or one half) (or two thirds)
How much of a sandwich is 2/3? 3/4? 5/8? etc.
Session Four
In this session, students work from part to whole. Usually students encounter problems where the whole is well-defined, and they are shown, or must create, the required fraction. As they progress to more complex tasks, it is also important that students can relate a fraction-part back to the whole from which that part may have been created.
Suppose there are eight Teddy Bears at the picnic. This piece is one eighth of a sandwich, how can we find the size of the whole sandwich?
How can we check [Name]’s estimate of the whole sandwich?
This is one fifth of the banana. How long is the banana?
This is one third of the doughnut. How big is the doughnut?
This is one half of the bun. How big is the bun?
This is one sixth of the chocolate cake. How big is the cake?
This is one quarter of the packet of walnuts. How many walnuts are in the whole packet?
Independent work
I will make a chart with this pretend piece of food.
Provide the students with a copy of Copymaster 5 to reduce the writing load.
Session Five
In this session, students connect fractions of regions and fractions of sets. Partitioning of a set into equal parts fluently requires multiplicative thinking that most young students do not possess yet. However, exposure to problems with equal partitioning provides opportunities to learn that develop additive part-whole thinking and the ‘sets of equal sets’ concept, that is fundamental to multiplication and division.
How many smarties do you think go on each quarter? Remember that the quarters must be equal.
Let’s imagine there are three smarties on each quarter. How many smarties would that be on the whole cake?
Last time the cake was in quarters. What fractions is it in now? (fifths)
Will the five Teddy Bears get more or less than four Teddy Bears got?
How many smarties are on the cake?
If I put two smarties on each fifth how many would be on the whole cake?
How many smarties can I put on each fifth?
Dear family and whānau,
This week we are exploring fractions in a story about the Teddy Bears’ Picnic. We know that fractions come from splitting one thing into equal parts. The number of parts we make tells us the name of the fraction. For example, if we split one into four parts, we make quarters or fourths.
You can support your child with this learning by asking them to split drawings of shapes into various equal parts, and then having them recreate what a whole may look like of other shapes (if the shape was a part, such as a half or quarter).
Ways to Add
In this unit students explore different ways to communicate and explain adding numbers within ten and beyond. The representations included are number lines, set diagrams, animal strips and tens frames.
In this unit students are introduced to different ways to represent the addition of single digit numbers using sentences, equations and number lines. Students will be able to communicate their thinking using the representations.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. The difficulty of tasks can be varied in many ways including:
The contexts for this unit are a tens frame waka and native animals. The materials can be adapted to suit cultural knowledge and interests of your students. Using physical items that have significance to your students might be more engaging than using standard mathematical equipment. For example, if you have a big set of shells or stones for environmental studies you might use those shells as the materials for session 1. You might create ‘story shells’ that are appropriate to your students, such as hatchlings in a nest, baked goods in a tray, whanau members in whare, or people at a feast.
Session 1
In this session students are introduced to using a diagram or picture to communicate an addition equation. You may need to adjust the numbers used in the lesson in response to the knowledge of your students.
How many kaihoe/rowers are in the waka?
Place 2 red counters in the tens frame and ask:
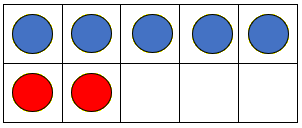
How many kaihoe/rowers are in the waka now?
Students may count from one, i.e. 1, 2, 3, 4, 5, 6, 7.
Some students will be able to count on from the five i.e. 5... 6, 7.
Using two different colours will help encourage students to count on and support subitising (recognising 7 counters instantly).
How many kaihoe/rowers are in this waka?
Count with me as I add more kaihoe/rowers.
How many kaihoe are in the waka now?
How many red counters did we put in?
How many blue counters are there? (Write 5 in blue.)
And how many red counters are there? (Write 3 in red)
5 and 3 makes how many counters?
Record the equation 5 + 3 = 8.
Session 2
In this session students continue to use tens frames to represent addition equations. They work on simple “change unknown” problems (e.g. 8 + □ = 10) in this lesson. You need a set of tens frames with dots. These can be made using the Copymaster.
Show students the waka model. How many kaihoe can get in the waka? How do you know?
Some students may recognise that 5 + 5 = 10.
Show the students a tens frame waka with 6 kaihoe. For example:
How many kaihoe are in the waka?
The waka needs a full crew. How many more kaihoe do we need?
Students may be able to image 4 more dots and then count all the dots, or they may need you draw the 4 dots before they can count all the dots. Consider providing physical materials (e.g. counters) for those who need it.
4 + □ = 7
Session 3
In this session students are introduced to Animal strips as a way to communicate addition equations. The animals are native to Aotearoa/New Zealand.
How many animals are on the strip?
How many animals are on the strip?
How many animals are there altogether?
Session 4
In this session students are introduced to the number line as a way to represent addition problems.
"I am making a putiputi (woven harakeke flower). I pick 4 strips of harakeke. Then I pick another 3 strips of harakeke. How many strips of harakeke do I have?
Expect students to tell you that the total is 7.
Draw a number line above the number strip as shown below. Highlight that the numbers go at the end of the counters, not the middle as you might do when pointing to the counters.
Remove the number strip and counters so only the number line remains.
What numbers have I written?
Why did I only write those numbers?
Session 5
In this session students consolidate their use of representations. Provide them with an open people to solve, such as:
Mihi collected some paua in the morning and some more paua in the afternoon.
She collected 12 paua altogether. How many paua did she collect in the afternoon?
6 and 6 equals 12
6 + 6 = 12
Let students explore possible solutions. Encourage them to use as many representations as possible. Some students may need support with counters and numbers strips.
Can you find all the answers? How will you do that?
After a suitable time, record all the answers students found. Organise the equations systematically.
1 + 11 = 12
2 + 10 = 12
3 + 9 = 12
….
9 + 3 = 12
10 + 2 = 12
11 + 1 = 12
Ask students what patterns they notice. Can they explain why the patterns occur?
If time permits, use the same scenario to explore change-unknown addition problems.
Mihi collected 5 paua in the morning and some more paua in the afternoon.
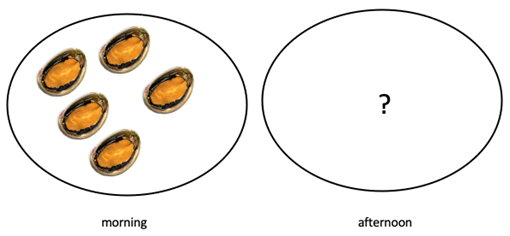

She collected 9 paua altogether. How many paua did she collect in the afternoon?
Change unknown problems can be represented using a number line and equation.
5 + ㅁ = 9
For high achievers explore start-unknown addition problems such as:
Mihi has some paua. She gets 4 more paua. Now she has 10 paua.
How many did she have to start with?
Dear family and whānau,
This week in maths we have been using different representations to show addition number sentences. One way is using a set diagram, and then writing a number sentence (equation) to go with it:
6 + 4 = 10 or 6 and 4 equals 10
With your child draw some other set diagrams using 2 colours and record addition equations. This will help your child to understand addition.
Taller/Wider/Longer
This unit encourages students to use measurement language and counting to compare the attributes of length, width or height of objects in a variety of game situations. The transition from counting all to advanced counting is also supported.
Measuring is about making a comparison between what is being measured and a suitable measurement unit. The first step in the measuring process is understanding that objects have attributes that can be measured. Initial experiences are needed to develop awareness of the attribute and to introduce the necessary language, for example, long, longer, short, shorter, tall, taller, wide, wider, narrow, narrower.
The activities in this unit provide experience in using measurement vocabulary.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. The difficulty of tasks can be varied in many ways including:
The contexts for this unit can be adapted to suit the interests and experiences of your students. For example:
Te reo Māori vocabulary terms such as tāroaroa (tall - person), poto (short), tāroaroa (height of a person), teitei (height, tall), whānui (wide, width), whāiti (narrow) roa (long, length) could be introduced in this unit and used throughout other mathematical learning. Numbers in te reo Māori can be used alongside English throughout the unit.
Session 1
In this session we introduce the language of comparison that will be used throughout the unit.
Are they tall?
Who is taller?
Compare the heights of the two students to see who is taller.
Ensure that all students understand that taller means more tall than.
Is my string longer?
Is my string shorter?
The following three sessions provide games in which students will practice the language of comparison.The games could be introduced in three separate sessions or all be introduced in one session and then played in groups rotating over several sessions. These games are also suitable to go into a general box for early finishers to use during other maths lessons.
Session 2: Wiggly Worms
Wiggly Worms is about the language of length. Students will be encouraged to use the words long, short, longer, shorter, longest, shortest.
Session 3: Tremendous Trees
Tremendous Trees is about the language of height, students will be encouraged to use the words tall, short, taller, shorter, tallest, shortest.
Session 4: Wonderful Walls
Wonderful Walls is about the language of width, students will be encouraged to use the words wide, narrow, wider, narrower, widest, narrowest.
Session 5: Reflection
Dear parents and whānau,
In maths this week we are studying measurement and we are learning to use the language of comparison. You can help by asking your child plenty of questions that use the words taller, shorter, longer, wider, and narrower. For instance, “Which is wider, the bench or the kitchen table?”, “Which is taller, the cat or the dog?” "Which is longer, your book or mine?" If you speak a language other than English at home, encourage your child to bring some phrases around the words taller, shorter, longer, wider, and narrower to school. We can share and practice using these as a class.
Inequality symbols and relationships
The purpose of this unit of three session is to develop understanding of how to recognise and record relationships of (equality and) inequality in mathematical situations.
The first relationship symbol that most students encounter is the equals symbol, =, which communicates a relationship of equivalence between amounts. It is important for students to understand that symbols help us to express relationships between numbers and that equivalence is just one such relationship.
Inequality is the relationship that holds between two values when they are different. Their relative value is described with specific language including ‘is greater than’, ‘is more than’, ‘is bigger than’ or ‘is less than ‘ or ‘is fewer than’. These are expressed using the symbols, <, >, which are said to show ‘strict’ relationships of inequality. Whilst not introduced here, the symbols, ≤ , meaning ‘is less than or equal to’, and , ≥, meaning ‘is greater than or equal to’, are known as ‘not strict’. The notation ≠, meaning ‘is not equal to’ is briefly introduced here as it is a useful, if infrequently used, relationship symbol.
Algebra is the area of mathematics that uses letters and symbols to represent numbers, points and other objects, as well as the relationships between them. Through exploring both equality and inequality relationships, and the symbols used to express these, students develop an important and heightened awareness of the relational aspect of mathematics, rather than simply holding the computational view of mathematics that arises from the arithmetic emphasis that is dominant in many classrooms.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. The difficulty of tasks can be varied in many ways including:
The contexts for this unit can be adapted to suit the interests and experiences of your students. For example:
Session 1
SLOs:
Activity 1
Elicit descriptive, comparative language: tall, taller, tallest, short, shorter, shortest, same).
Point out that we have been comparing and describing the buildings in relation to one another and explain that we will now be investigating relationships between numbers.
For example, one student takes seven pink cubes.
Place a simple city street map in front of the students, or create one with them.
Have the students join their cubes to make buildings for this city. When they have made their ‘tower buildings’, have them locate them, standing up, in places of their choice between the streets, creating a ‘cityscape'. If adapting to use native forest, rivers and streams could replace the roads of the street map, and cubes can become 'trees'. This adaptation would be continued on throughout the remainder of the sessions and activities.
Read the equation together, “Five is equal to five” and “Five is the same as five.”
The buildings are then returned to their place ‘in the city’.
Have a student describe how these numbers (of storeys) are ‘related’: “six is more than four”, “four is less than six”, “six is not equal to four.” Ask, “How can you write this?” Record the students’ suggestions, accepting all ideas.
Have students identify more ‘unequal buildings’ and record these as inequality statements on the chart and read them.
If possible retain the class ‘cityscape’ for Session 2.
Activity 2
Have student pairs retain their maps for Session 2.
Activity 3
Conclude the session by having the students share their recording and discussing how the symbols = and ≠ show us how numbers are related to each other.
Photograph the class and pair ‘city models’ to display with student recording from Activity 2, and from further sessions.
Session 2
SLOs:
Activity 1
Explain that there are more relationship symbols and that they will learn about two more in this session.
6 ≠ 4
Have student pairs discuss the towers
then, as a class, record their observations, including ‘6 is more than 4’ and ‘4 is less than 6.’ Ask if anyone knows symbols that show each of these relationships.
< >
Write the words, ‘is more than’, and ‘is greater than’, together on the class chart, and ‘is less than’ or ‘is fewer than’ together.
Have students discuss these in pairs and decide which symbol goes with which pair of phrases and why they think that.
Activity 2
Each student is to write at least four inequality cards for pairs of ‘buildings’. For example:
Activity 3
"Four is less than/is fewer than 6"
Each student should now have written at least 4 pairs of cards; 16 cards in total for the pair.
Activity 4
Each pair is to play a short Memory game with these cards by spreading them out face down in front of them and trying to find matching pairs of statements. For example:
Activity 5
Conclude the session by reviewing the four relationship symbols (one of equality and three of inequality) that have been used in Sessions 1 and 2.
=, ≠, <, >.
Retain student ‘cities’ and relationship cards for Session 3.
Session 3
SLOs:
Activity 1
Explain that the students must listen very carefully to the story. As they do so, they should record relationship expressions, in order, for any numbers that they hear. Read the story once. Highlight an example (eg. 3 >2 weetbix) and read the story again.
Activity 2
For each discuss and record the difference. For example:
Weetbix: 3 > 2, 2 < 3,
Three is one more than two. Two is one less than three.
The difference is one.
Age: 60 > 50, 50 < 60
Sixty is ten more than fifty. Fifty is ten less than sixty.
The difference is ten.
Cats: 6 > 0, 0 < 6
Six is six more than zero. Zero is six less than six.
The difference is six.
Dog: 1 = 1
One is the same as one. There is no difference.
The difference is zero.
Activity 3
Display two ‘towers’ from the class ‘city’. Ask. “What is the difference between the two towers? How do you know?” For example:
Show:
Elicit explanations such as 'there are two more green ones, there are two less/fewer yellow ones'.
Write 6 – 4 = 2 on the class chart and on a card.
Highlight the fact that when we solve a subtraction problem we are finding the difference.
Explain that they are to write a difference card and a subtraction equation card as shown in Activity 3, Step 1 for each of their inequality expression pairs. Have partners check each other’s cards.
For the pair, there are now 32 cards in total, 8 sets of four cards.
These can be put together in a bag, or combined with an elastic band.
Purpose: To recognise equivalent pairs of inequality expressions, and their matching subtraction equation and difference statements.
How to play:
Cards are shuffled. Five are dealt to each player. The spare cards are put in a pile, face down, handy to all players.
Players check to see if they have any complete sets in their hand. If so, these are displayed face up in front of them. Each player then privately identifies which set they will collect and they take turns to ask one other named player for a specific card to complete their set.
For example:
In hand:
At their turn, the player says, “Name, do you have the card, four is less than six?”
If the named player has the card, they must forfeit it. The successful player can ask again till they are told, “No. Go fish.” That player then takes a card from the top of the upturned pile of spare cards. It is then the turn of the next player.
The winner is the player with the most complete sets when all cards are used.
Activity 4
Conclude this session by reviewing key learning from this series of three lessons. Sets of cards can be used as an independent consolidation task.
Dear parents and whānau,
In maths we mostly write equations. These use the equals (=) symbol. This symbol tells us that two amounts are equivalent. However sometimes numbers or amounts are not equal.
In maths this week, the students have been learning how to record inequality expressions such as 8 > 6, (eight is greater than or more than six) and 6 < 8 (six is less than or fewer than eight.) They have also learned to find the difference between numbers by solving a subtraction equation (in this case 8 – 6 = 2) and to state the difference (the difference is 2).
They have made their own card games to play with you at home.
Your child will explain how to play Fish for Four.
We hope you enjoy playing Fish for Four, and enjoy helping your child to practice their learning about inequality expressions and number relationships.