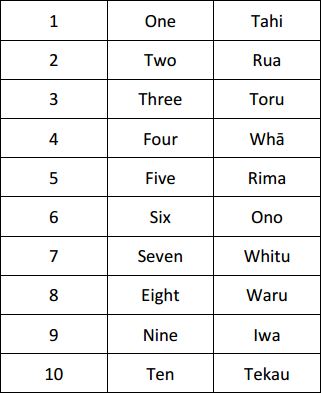
The purpose of this unit of sequenced lessons is to develop knowledge and understanding of combinations to ten.
- Explore the numerals to ten.
- Instantly recognise patterns within and for ten.
- Make and record groupings within and for ten.
- Recall and apply groupings to ten using te reo Māori.
- Recognise the usefulness of just knowing combinations to ten.
- Use an ‘if I know ___, then I know___’ approach to solving number problems.
These lessons build upon the student’s recognition and knowledge of groupings within ten, to scaffold ready combinations and separations in numbers that make ten.
A goal within primary mathematics is for students to use partitioning strategies when operating on numbers. By building images and knowledge of these combinations at an early age, the ability to naturally partition larger numbers will be strengthened. Students should have many opportunities to combine and separate numbers to ten and come to clearly see and understand how these ‘basic facts’ are fundamental building blocks of our number system.
As they work with numbers greater than ten, students will develop knowledge of ‘tidy numbers’ and about ‘rounding to ten’. Students should be encouraged to know and have an intuitive feeling for "ten". Ultimately, they should be able to readily apply this knowledge in solving problems that involve partitioning and combining larger numbers and sets.
Our place value system has ten digits only. It is the place of a digit in a number that determines its value. Ten is the basis of this system. By having the opportunity to briefly explore other number systems (Roman and Mayan), and by considering notation to create their own system, students will better understand the numerals and number representations that we may take for granted within the base ten system we use.
The activities suggested in this series of lessons can form the basis of independent practice tasks.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- providing more practice with the tens frames to develop the students knowledge of the number facts to 10. Encourage them to subitise (to recognise, without counting) the number of counters and the number of gaps.
- spreading session 4 over two or more sessions if the students are unfamiliar with the Māori numbers to ten
The contexts for this unit can be adapted to suit the experiences of your students. For example, numbers to ten in other languages can be used in this unit in response to the languages and cultures of your students. For example: numbers from Pasifika cultures could be included in a similar way to how te reo Māori is used in session 4.
Te reo Māori vocabulary terms such as mati (digit) and meka matua (basic facts) could be introduced in this unit and used throughout other mathematical learning.
- Slavonic abacus
- Tens frames
- Copymaster 1
- Copymaster 2
Session 1
SLO: Explore the numerals to ten.
Activity 1
- Make paper, crayons/felts, pencils, counters (or similar mathematics equipment) available to the students. Set a time limit as appropriate. Have the students write, draw and show you everything they know about ten.
- Have the students pair share their work.
- Write the word ‘ten’ and the numeral 10 on chart paper or in a modeling book. Collect and record the important ideas that the students have generated. Be sure to use words, symbols and drawings of equations, stories or materials.
- Highlight the fact that in our systems we have ten digits which we ‘reuse’ (for example, the number 10 is made up of the numbers one and zero). On the board show the students 1, 10 and 100 as an example.
- Ask if the students know why ten is an important number. Accept the student ideas and say they will be learning more about why ten is so important.
Activity 2
- Explain that the class will look briefly at other number systems. Locate Italy on a map, show where Rome is and explain that many hundreds of years ago these people, the Romans, wrote numerals to ten this way.
- Have the students talk in pairs about what they see. Record all their ideas.
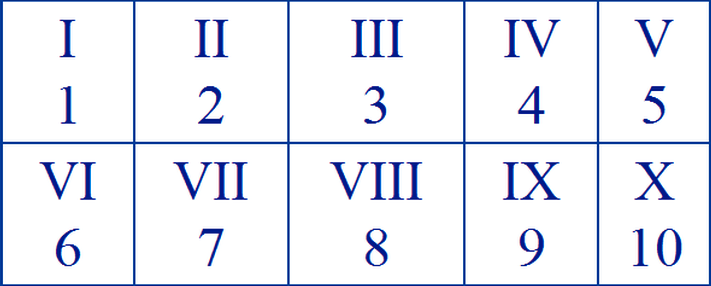
- Talk about the similarities and differences in the way we record ten now, 10 compared with X (ten has its own unique symbol).
- Locate Mexico and Central America on a map. Explain that the Mayan people who lived there hundreds of years ago used these symbols. Have the students talk in pairs about what they see. Record all their ideas.
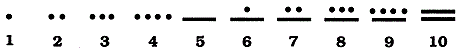
- Talk about the similarities and differences in the way we record ten now, compared with the Mayan symbol. Discuss why ten is recorded in this way.
- Have students in pairs invent and record their own numerals to ten. Have them write some simple equations using their symbols, then share their numeral system with another group.
- Conclude by reviewing different ways of writing ten. Highlight the fact that in our system we have just ten numerals which we ‘reuse’.
Sessions 2-3
SLOs:
- Instantly recognise and describe patterns within and for ten.
- Make and record groupings within and for ten.
- Review families of facts within ten (introduced in the Using five unit).
Introduce the following activities over the next two sessions.
Activity 1
- Show a frame with ten dots.

Have the students show ten on their fingers, then have them describe to a partner how many dots they see and how many fingers they see, using ‘ten and no more.’ Record 10 + 0 = 10
- Show other tens frames out of order. Direct students to take turns with a partner. Each turn, they should say how many dots they see and describe what they see on the tens frame. For example, “Eight. That’s five dots, and three dots and two empty spaces. That's eight dots and two spaces.” Model this for the class before allowing them to work in pairs. Consider organising the pairs to group together students with mixed mathematical abilities. There may be some students who would prefer to work with the teacher in a small group whilst the rest of the class works in pairs.

- Record several examples as a class using words and symbols. Seven dots and three spaces, four dots and six spaces, one dot and nine spaces.
Record equations with unknowns representing some of the tens frames; For example, for dots: 7 + ☐ = 10, 10 = 4 + ☐, 10 = 1 + ☐
Make it clear that the spaces ask us ‘how many more to make ten?’
- Model using two different coloured counters to fill the spaces, showing and saying ‘seven dots plus three dots is the same as ten dots’.

Record equations, 7 + 3 = 10 and 3 + 7 = 10.
Ask what subtraction equations can be recorded using these numbers. Accept student responses, write and model by removing counters, 10 – 3 = 7 and 10 – 7 = 3
Highlight that the four equations are related because they use the same 3 numbers. They are known as a family of facts.
Model with other tens frames: for example 10 = 4 + 6, 6 + 4 = 10, 10 – 4 = 6 and 10 – 6 = 4.
- Hold up the tens frames in random order. Direct students to call out how many dots they see then record with a “magic finger” on the mat or with writing materials how many more to make ten. For example, show:

Students say, “Eight,” and write 2. Students with emergent writing skills could be paired with a student with more developed writing skills, or could use counters to demonstrate their understanding of how many more are needed to make ten.
Activity 2
Students play Clever Fingers in pairs. (Purpose: to practice seeing, saying and writing combinations to ten)
They need ten counters, pencil and paper to record winning equations. For each “hand” played they move a counter into a ‘used’ pile.
Students, with their hands behind their backs, make a number on their fingers.




They take turns to call ‘Go.’ On ‘Go’ they show their fingers. If the combination of raised fingers makes ten, they say, “Clever fingers” and one student records the equation. 3 + 7 = 10 When all the counters are used (they have had ten turns). They count their equations. Student pairs compare results.
Activity 3
Students play Snap for Ten in pairs.
(Purpose: to practice seeing, saying combinations to ten)
They need playing cards with Kings and Jacks removed, and use the Queen as a zero.
Turn over a card to begin the game.
Students take turns to turn over a card from the pack, placing the turned card on top of the card before. If the turned card can combine in some way with the previous card to make ten the student says, ‘Snap’, states the equation and collects the pile of cards.
For example: if 9 is turned, followed by a 1, 9 + 1 = 10 is stated and the pile of cards is collected.
Activity 4
Students play Memory Tens in pairs..
(Purpose: to practice seeing and saying combinations to ten)
They need playing cards with Kings and Jacks removed, and use the Queen as a zero.
Cards are turned down and spread out in front of the students.
Students take turns to draw pairs. If the numbers on the two cards combined make ten, the pair is kept by the player.
For example: A player draws 6 and 4 and states 6 + 4 = 10 and keeps the pair.
The game continues till all cards are used up.
The winner is the person with the most pairs.
Activity 5
Students play Fast Families
(Purpose: to practice writing and demonstrating family of fact combinations to ten)
They need pencil and paper.
Students place ten counters of one colour on a blank tens frame.
They take turns to roll a ten-sided dice. The dice roller removes the number of counters indicated by the dice roll and says, “Go.”
The players quickly write the four family of fact members associated with 10, 6 and 4: beginning with the equation just modeled.
10 – 6 = 4, 6 + 4 = 10, 10 – 4 = 6, 4 + 6 = 10.
The first to write these calls stop.
That player chooses another player to demonstrate and say the other three family members in logical order by adding 6 onto the 4, saying 4 + 6 = 10, then removing 4 counters saying 10 – 4 = 6 and finally adding 4 back onto the 6 and saying 6 + 4 = 10.
If this player is correct, he rolls the dice and the game begins again.
The winner is the student who accurately records the most families of facts.
Session 4
SLO: Recall and apply groupings to ten using te reo Māori.
- Students count in te reo Māori up to and back from ten: “Tahi, rua, toru, whā, rima, ono, whitu, waru, iwa, tekau. Tekau, iwa, waru, whitu, ono, rima, whā, toru, rua, tahi.”
If students are unfamiliar with nga tau, have a number chart displayed.
Each student has a set of number words to ten in te reo Māori (Copymaster 1).
A ten-sided dice is passed around the class circle. Each student takes a turn to roll the dice and call the number in English and in Māori and classmates must hold up the Māori word.
- Students play in pairs Nga Tau Pairs
(Purpose: to recognise and come to know number words in te reo Māori)
A mixed piles of tens frames are provided with a mixed pile of Māori number word cards to ten.
Both are turned down. The students take turns turning over a tens frame and a word card. If they match they keep the pair.
The winner is the player who has the most pairs when all the cards are used.
- Students play in pairs Total Tekau (like Snap for Ten)
(Purpose: to recognise and come to know number combinations to ten using Māori number words)
Each student shuffles a double set of Māori number word cards to ten and places the pile face down in front of them.
They take turns to turn over one word card at a time and place these in one pile, one on top of another. If two consecutive numbers together make ten, the player who played the second card calls, ‘Tekau’ and collects the whole pile and begins the game again.
The winner is the player with all the cards or with the biggest pile when the game is stopped.
Session 5
SLO: Recognise the usefulness of knowing combinations to ten.
- Review and practice known facts.
Have a set of tens frames displayed to support some students.
Provide each student with a number fan.
As the teacher shows a digit, each student finds and shows the complementary digit to ten.
For example: the teacher shows 3 and each student shows 7.
- The teacher records subtraction problems and has the students find and show the result.
For example, the teacher writes 10 – 2 = ☐ and the students show 8, the teacher writes ☐ - 5 = 5 and the students show 10.
- Register students on e-ako Maths. Support them to become familiar with the addition and subtraction facts learning tool. This tool supports the student to learn unknown facts to ten by building on already known facts. Tens frames images are used. Students will need to be confident using a Chromebook/iPad/laptop to participate in this task.
- Introduce the term “basic facts”.
Ask the students, “What is a fact?” and record their responses. (A fact is something that has really occurred or is actually the case. It is something that can be tested and can be found to be true).
Ask the students, “What does ‘basic’ mean?” and record their responses. (Something that is basic is essential, fundamental. A ‘base’ is the bottom support of anything or the thing upon which other things rest. It is a foundation.)
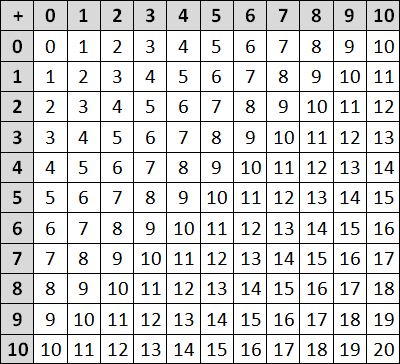
- Identify which are our basic addition and subtraction facts by showing this grid to the students and by exploring how it works. Draw focus to the basic facts that your students are familiar with. Students with more advanced knowledge may be able to share some of the basic facts they know, that make use of higher numbers, with the rest of the class.
- Highlight the importance of knowing combinations to ten and conclude with a game of Memory Tens, as played in session 2.
Session 6
SLOs:
- Recognise the usefulness of knowing combinations to ten.
- Use an ‘if I know, so I know’ approach to solving simple number problems.
- Review content of sessions 1 – 4. Focus on inverse operations of addition and subtraction as shown in the family of facts.
Demonstrate this by developing with the students and “If I know this, then I know that ” flow diagram. For example: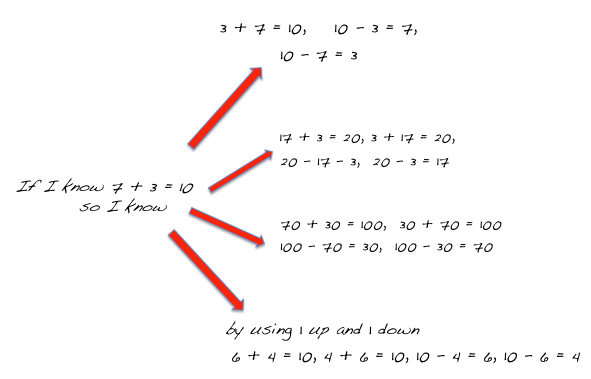
The students are being introduced to this idea. They are not expected to immediately apply the principle to the bigger numbers.
Highlight the important idea that maths is about relationships between numbers, like fact families, and if we look for these and for number patterns, they help us.
- Begin to complete the addition grid together. Write a sentence together describing something the students notice.
Have students complete their own copies of the grid (Copymaster 2) and write (up to) five things they notice.
Have them share with a partner what they have discovered.
- As a class, discuss and record the students’ ‘discoveries’. Make a list together of how knowing about these patterns helps us.
- On their own paper, have the students each write their own favourite equation within or to ten. Have them create their own “if I know this, then I know that" brainstorm chart as modelled in 5a.
Dear parents and whānau,
In class we have been making, saying and practising addition and subtraction facts with numbers up to ten.
Your child can access practice tasks on the e-ako maths website: https://e-ako.nzmaths.co.nz/ if this suits your family arrangements.
Your child would also enjoy sharing with you activities they have learned in class and would appreciate your making time to play a maths games with them. Here are two we have played in class. You might like to make up one of your own too.
Memory Tens.
In pairs, using playing cards with Kings and Jacks removed, and using the Queen as a zero:
Cards are turned down and spread out in front of the players.
Players take turns to draw pairs. If the numbers on the two cards combined make ten, the pair is kept by the player.
For example: A player draws 6 and 4 and states 6 + 4 = 10 and keeps the pair.
The game continues till all cards are used up.
The winner is the person with the most pairs.
Snap for Ten.
In pairs, using playing cards with Kings and Jacks removed, and using the Queen as a zero:
Turn over a card to begin the game.
Players take turns to turn over a card from the pack, placing the turned card on top of the card before. If the turned card can combine in some way with the previous card to make ten the student says, ‘Snap’, states the equation and collects the pile of cards.
For example: if 9 is turned, followed by a 1, 9 + 1 = 10 is stated and the pile of cards is collected.
The winner is the person with the most cards.