This unit supports students to equally partition objects and sets into fractional parts.
- Partition a length, area or volume into equal parts.
- Partition a set into equal parts and anticipate the result.
- Recognise that the numerator of a fraction is a count.
- Recognise that the bottom number of a fraction gives the size of the parts being counted.
In this unit students explore equal partitioning of objects and sets, and how to name the parts they create using fractions. The easiest partitions are those related to halving since symmetry can be used. For example: halves come from partitioning a whole into two equal parts, and quarters come from partitioning a whole into four equal parts.
An object is partitioned according to an attribute, or characteristic. For example, a banana might be partitioned by length, but a sandwich partitioned by area. Some attributes are more difficult to work with than others. Length is the easiest attribute but others such as area, volume (capacity), and time are more difficult.
The results of partitioning a set into fraction parts can be anticipated, using number knowledge and strategies. For example, one quarter of 20 could be found by:
- organising 20 objects into four quarters one by one, or in collections of two
- halving 20 into 10, then halving again
- realising that putting one object on each quarter uses four each time, and repeatedly adding four until 20 is used up.
In this unit we apply three criteria when evaluating students’ capacity to partition and object or set into fractional parts:
- the correct number of parts is created
- the shares are equal
- the whole is exhausted (used up).
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. The difficulty of tasks can be varied in many ways including:
- encouraging students to work collaboratively in partnerships
- pausing to allow students to share their work with others
- using play dough, cardboard, or other physical materials to model key concepts
- restricting or extending the range of fractions students are asked to work with.
The contexts for this unit can be adapted to suit the interests and experiences of your students. For example:
- the first slide of PowerPoint 1 could easily be replaced to change the whole context of the unit to be about any different characters you choose
- preferences for different types of bread can invoke a good discussion. For example white or brown bread, rewena or pita
- more types of food could be added to better reflect the food your students usually eat.
Te reo Māori vocabulary terms such as hautau (fraction), ōrite (equal), haurua (half), hauwha (quarter), hautoru (third) and toha (share) as well as counting from kore ki tekau (zero to 10) could be introduced in this unit and used throughout other mathematical learning. Other te reo Maori that could be useful in this unit are teti pea (teddy bear) and hanawiti (sandwich).
- Teddy Bears (brought from home) or Teddy Bear counters
- Pattern blocks or Attribute blocks
- Play dough and plastic knives
- Counters or cubes
- Blank wooden cubes (to make dice)
- Apple, doughnut, banana, bread (optional)
- Clear plastic drink bottle and plastic cups
- Scissors
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- Copymaster 6
- PowerPoint 1
- Powerpoint 2
- PowerPoint 3
Session One
- Use PowerPoint 1 to tell the story of two teddy bears going on a picnic. Unfortunately, Pāpā Bear, who made the lunch, forgot to cut up the food items equally. What are Rawiri and Hine Bear supposed to do?
Rawiri and Hine are friends. They always share their food equally. How could they cut this sandwich? (Slide Two) - Discuss ways to cut the sandwich in two equal pieces. Having two teddy bears available allows for acting out the equal sharing.
What does equal mean?
What do we call these pieces? (halves) - Write the words “one half” and the symbol 1/2.
Why do you think there is a 1 and a 2? (2 refers to the number of those parts that make one) - Look at Slides Three and Four of PowerPoint 1.
Is the sandwich cut in half? Why? Why not? - Provide the students with three ‘sandwiches’ made from Copymaster 1.
What other ways could Rawiri and Hine cut their sandwich in half? - For students who complete the task quickly, give them another sandwich.
Cut this sandwich in two pieces that are not halves. - When each student has produced at least two halved sandwiches bring the class together to share their thinking. Make a collection of halves and ‘non-halves’ and discuss those collections.
What is true for the sandwiches that are cut in half?
What is the same or the sandwiches that are not cut in half?
The key idea of halving is that both Rawiri and Hine get the same amount of sandwich. As the sandwich is not exactly symmetric through a horizontal mirror line you might get interesting conversation about the equality of shares. Slide Five may provide some stimulus for the discussion. Using the cut-out pieces of sandwich, show how halves map onto each other by reflection (flipping) or rotating (turning). With paper sandwiches you can fold to show that mapping of one half onto another. - Luckily Pāpā Bear prepared more than just one sandwich. Copymaster 2 has some other food items that Papa packed. Ask your students to work in pairs to cut each item in half. They need to record where they will cut each item and justify why they put the line where they did.
- After enough time bring the class together and discuss their answers. Act out the halving, either with real objects or imitations, e.g. banana and cheese made from playdough of plasticine. This is particularly important in the case of the bottle of fruit drink and the bag of 12 cashews. Note there are different ways to partition each object into two equal parts. Points to note are:
- Do your students create two parts, exhaust all of the objects or set, and check that the parts are equal in size?
- Do your students see halving as a balancing, symmetric process?
- As an example, get two clear plastic cups. Ask a student to pour half of the drink bottle into each cup, one for Rawiri and one for Hine. Look to see that the student balances the level in each cup. Capacity is a perceptually difficult attribute for measurement.
- Similarly, look to see if students equally share the cashews by one to one dealing.
- Finish the session with the final two slides of PowerPoint 1.
Can your students distinguish when a shape or set has been halved?
Session Two
In this session, students explore the impact of other Teddy Bears joining in the picnic. What happens to the size of the portions as more shares are needed? How do we name the shares?
- Remind the students about the previous session. Use a chart of halves and ‘not halves’ to focus attention on equal sharing and the words and symbols for one half.
Imagine that four Teddy Bears went on the picnic instead of two. Pāpā still packed the same amount of food. What would happen then? - Sit four teddy bears around in a circle. Give them names like Rawiri, Hine, Aleki and Sina. Use Copymaster 1 to make a few sandwiches.
How could we cut a sandwich into four equal parts? What will the parts be called? - Students should find quartering intuitive, as it involves halving halves. Symmetry is still useful. Let students share how they think a sandwich could be partitioned into four equal parts. Act out giving one part to each Teddy Bear.
Does each Teddy Bear get the same amount of sandwich?
Common solutions are: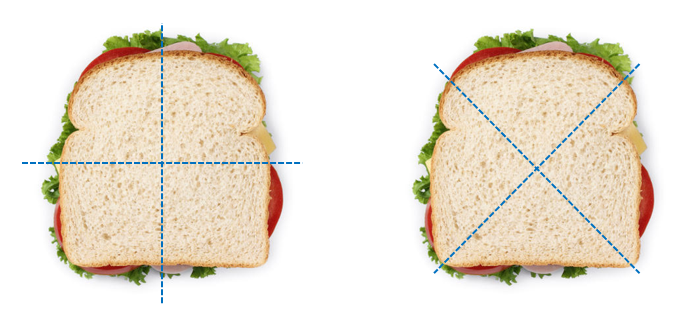
Students often miss the option of dividing the area of the sandwich by length…
Or other possibilities…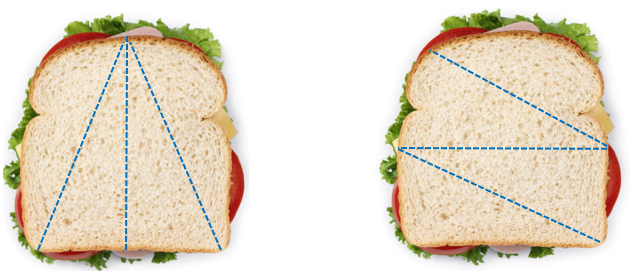
- Ask students: How big is one quarter/fourths, compared to one half? How many quarters is the same as one half?
- Use pieces of’ ‘sandwich’ to check. It is good for students to see that two quarters make one half irrespective of the shape of the pieces. Challenge the students to find some ways to cut a sandwich into four pieces that are not quarters. Examples might be:

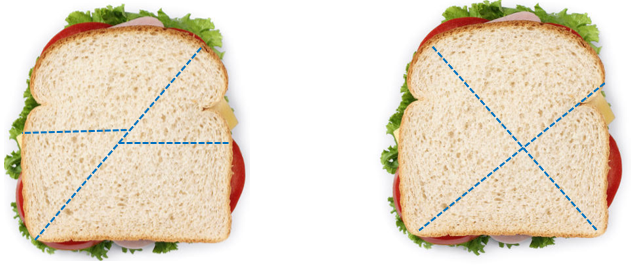
- You may need to highlight the lack of equality of non-quarters by mapping the pieces on top of one another. Discuss that quarters are only quarters if:
- four pieces are made
- all the sandwich is used
- the pieces are all equal in size.
- Provide the students with copies of Copymaster 2 again.
This time the challenge is to share each picnic food into quarters. - Give the students enough time to record where they would partition the items before gathering as a class to discuss their ideas. Pay attention to the different ways that the foods are partitioned. Act out the partitioning either with real objects or imitations, e.g. banana and cheese made from playdough of plasticine. For example, the banana is a length, so the partitioning is most likely to be by length. Some students may attend to area (second example):
 or
or 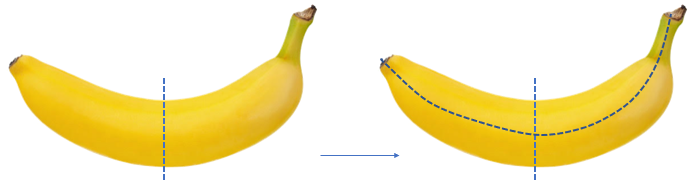
The shape of the sector of cheese places a restriction on how it can be partitioned. Likely responses are (left is correct, right is not):

- Equally sharing the bottle of fruit juice among four glasses might be done in two main ways:
- set out four plastic cups and keep pouring while balancing the water levels
- halve the bottle into two plastic cups. Pour half of each cup into another cup until the levels match.
- Look to see that your students can equally share the 12 cashews by dealing one to one for each teddy bear. Highlight that the half share is six cashews and the quarter share is three cashews.
- Record the words and symbols for one quarter. Create a chart of quarters for the food items.
Finish the session with the game called ‘Make a whole sandwich.” Students need copies of the first page of Copymaster 3 (halves and quarters) and a blank dice labelled, 1/2, 1/2, 14, 2/4, 3/4 and choose. The aim of the game is for players to make as many whole sandwiches as they can.
Players take turns to:- roll the dice
- take the amount of sandwich shown on the dice, e.g. if 3/4 comes up, then the player takes three one quarter pieces of sandwich
- if 'choose' comes up the player chooses any single piece.
At any time a player can rearrange their sandwich pieces to make as many whole sandwiches as possible. Time the game to finish in five minutes which is long enough to gather a lot of pieces.
- Discuss what might be learned from the game. For example:
- three quarters is three lots of one quarter
- two quarters is the same amount as one half
- two halves and four quarters both make one whole.
- Record those findings symbolically and discuss the meaning of + and = as joining and “is the same amount as”, e.g. 3/4 = 1/4 + 1/4 + 1/4 or 2/4 = 1/2.
Session Three
In this session, students explore the equal sharing of picnic foods among three Teddy Bears. Thirding an object or set is generally harder than quartering because symmetry is harder to use. Your students should observe that thirds of the same object or set are smaller than halves but larger than quarters.
- Begin with a reminder of what you did in the previous session:
We explored how to cut sandwiches into two and four equal parts. What are those parts called? (halves and quarters) - Be aware of the non-generality of early fraction words in English. Halves should be twoths, and quarters should be fourths, to match what occurs with sixths and further equal partitions. In many other languages, such as Maori and Japanese, the word for a fraction indicates the number of those parts that make one. Maori for one fifth is haurima (rima means five) and in Japanese one fifth is daigo (go means five).
What parts will we get if we share the food among three Teddy Bears? - Point out that third is a special English word for one of three equal parts. Show the students one half and one quarter of a sandwich.
Which is bigger, one half or one quarter? Why?
How big do you think one third will be? Why? - Students might conjecture that thirds are smaller than halves but bigger than quarters. That is true on the assumption that the whole (one) remains the same. Give the students copies of four ‘sandwiches’ from Copymaster 1. Set out three Teddy Bears.
Find different ways to share one sandwich equally among the three Teddy Bears. - PowerPoint 2 shows two examples and three non-examples of cutting a sandwich into thirds. Note that the successful cuts are vertical and horizontal. Students should notice that the two non-examples produce unequal parts. On slide five ask:
Is this sandwich cut into thirds? (No, the parts are unequal) - Give the students a copy of Copymaster 2. Ask them to work in pairs to share each food item into thirds. After a suitable period, bring the class together to discuss their equal sharing.
- PowerPoint 2 contains animations of partitioning some of the foods into thirds. You may want to act out model answers, certainly with pouring among three plastic glasses while keeping the levels balanced. Discuss issues that arise. For example:
Do the parts have to be the same shape to be equal? (Banana is a good example)
Why are thirds harder to make than halves and quarters? What other fractions would be hard to make? Why? - In the next part of the session, students anticipate the result of cutting thirds and quarters in half. What are the new pieces called?
PowerPoint 2- Slides 9-11, show how halving quarters produces eighths and halving thirds produces sixths. It is important for students to connect the naming of these equal parts to how many of those parts form one whole (sandwich). - Use parts of sandwiches made from Copymaster 3 to build up students’ counting knowledge of fractions. Lay down and join the same sized pieces and ask students to name the fraction. For example:

One sixth Two sixths Three sixths Four sixths
(or one third) (or one half) (or two thirds) - Count with the same sized parts past one whole and write the fraction symbols as you count.
How much of a sandwich is 2/3? 3/4? 5/8? etc. - It is important that students understand that the top number of a fraction (the numerator) is a count of equal parts. The bottom number (the denominator) tells how many of those parts make one.
- Change the game from session two called “Make a Whole sandwich.” Include all the pieces from Copymaster 3 so that thirds, sixths and eighths are also available. Alter the dice to read 1/2, 1/4, 1/3, 1/6, 1/8 and 'choose'. Allow the students more time to play that game (ten minutes).
- Discuss some ways that the students found to make one whole sandwich. Record their suggestions using symbols, e.g. 1/2 + 1/3 + 1/6 or 3/4 + 2/8. Begin a chart of ways to make one that students can add to using pictures (using pieces from Copymaster 3) and symbols.
Session Four
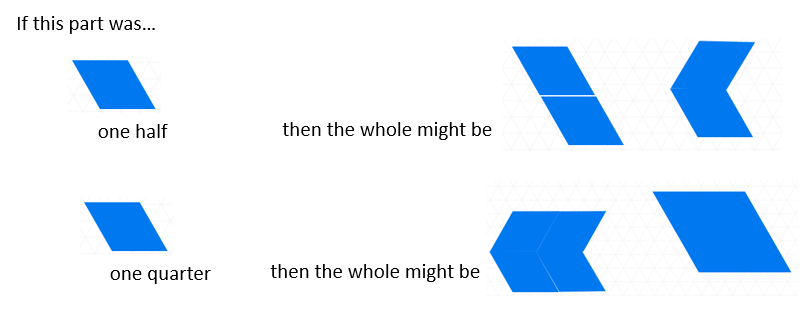
In this session, students work from part to whole. Usually students encounter problems where the whole is well-defined, and they are shown, or must create, the required fraction. As they progress to more complex tasks, it is also important that students can relate a fraction-part back to the whole from which that part may have been created.
- Use Copymaster 4 to create a set of paper part foods. With each challenge below, the aim is to draw the appearance of the whole, in schematic rather than detailed form. Place the fraction piece in the middle of an A3 sheet of photocopy paper to allow space to draw.
Suppose there are eight Teddy Bears at the picnic. This piece is one eighth of a sandwich, how can we find the size of the whole sandwich? - Check that students recognise that eight pieces of that size will make the complete sandwich. Ask a student to draw around the outside of the piece to show the whole sandwich.
How can we check [Name]’s estimate of the whole sandwich? - Iterating (copy and pasting) eight copies of the piece will give the area of the sandwich. Note that the whole could look differently as the eighths could be arranged on a line or as a rectangle or other formations. However, the context suggests a rectangular arrangement is best. Other challenges are:
This is one fifth of the banana. How long is the banana?
This is one third of the doughnut. How big is the doughnut?
This is one half of the bun. How big is the bun?
This is one sixth of the chocolate cake. How big is the cake?
This is one quarter of the packet of walnuts. How many walnuts are in the whole packet? - Build on the capacity example used earlier. Tell your students that a plastic cup filled to a certain level is one third, quarter, fifth, etc. of a whole bottle. Can they make the quantity of water that fills the bottle?
Independent work
- Show your students a set of pattern blocks. Choose one shape as ‘the piece of food’, e.g. a rhombus.
I will make a chart with this pretend piece of food. - Develop the chart as you go rather than present it as complete.
Provide the students with a copy of Copymaster 5 to reduce the writing load.
Session Five
In this session, students connect fractions of regions and fractions of sets. Partitioning of a set into equal parts fluently requires multiplicative thinking that most young students do not possess yet. However, exposure to problems with equal partitioning provides opportunities to learn that develop additive part-whole thinking and the ‘sets of equal sets’ concept, that is fundamental to multiplication and division.
- Use PowerPoint 3 to introduce the context of the four Teddy Bears sharing a chocolate cake.
How many smarties do you think go on each quarter? Remember that the quarters must be equal. - Students need to use their number understanding to anticipate a result. Some students may ‘virtually’ share the smarties one at a time (look for eye, hand and head gestures). Tracking the number of ‘virtual’ smarties in each quarter puts a significant load on working memory. Estimates of three, four or five should be worked with.
Let’s imagine there are three smarties on each quarter. How many smarties would that be on the whole cake? - Working from part to whole in this way checks the estimate. Using actual objects, like counters, to enact the sharing, might follow once anticipations are made and justified.
- Other students may use additive knowledge, such as 4 + 4 = 8 (one half), then 8 + 8 = 16 (whole cake). Students might adjust from an initial prediction, such as 20 smarties is four more than 16, so each quarter must get 4 + 1 = 5 smarties.
- Slide Two makes a minor adjustment to the number of shares to see if students can anticipate the effect of more parts on the size of shares. With five parts (fifths) additive knowledge with fives is more likely to be used.
Last time the cake was in quarters. What fractions is it in now? (fifths)
Will the five Teddy Bears get more or less than four Teddy Bears got? - Check that students recognise that fifths are smaller than quarters, even in the sets of smarties context. Encourage use of additive thinking by animating one smarty on each fifth of the cake.
How many smarties are on the cake?
If I put two smarties on each fifth how many would be on the whole cake?
How many smarties can I put on each fifth? - Slides Three and Four present two other situations of equally sharing smarties onto a cake. Ask your students to name the fraction parts and anticipate the result of the equal sharing.
- Let your students play the Birthday Cake Game in pairs or threes. The game is made from Copymaster 6. You will need blank dice and counters as well.
Dear family and whānau,
This week we are exploring fractions in a story about the Teddy Bears’ Picnic. We know that fractions come from splitting one thing into equal parts. The number of parts we make tells us the name of the fraction. For example, if we split one into four parts, we make quarters or fourths.
You can support your child with this learning by asking them to split drawings of shapes into various equal parts, and then having them recreate what a whole may look like of other shapes (if the shape was a part, such as a half or quarter).