Background Maths
Fractions involve a significant mental jump for the students because units of one,which are the basis of whole-number counting, need to be split up (partitioned) andrepackaged (re-unitised). It is crucial that the students have significant opportunitiesto split up ones through forming unit fractions with materials and are required torecombine several of these new units to form fractions like two-thirds and five quarters.
In this way, the students are required to co-ordinate the link between the numerator
and denominator in fraction symbols.
Early additive students are progressing towards multiplicative thinking. Fraction
contexts offer opportunities for these students to appreciate the links between addition
and multiplication. This can be achieved through requiring the students to anticipate
the results of equal sharing and involving fractions like thirds, fifths, and tenths,
where addition methods are less efficient.
It’s important that you require the students to construct the whole unit from given
parts. For example, if a student is given a Cuisenaire rod or pattern block and told that it’s one-quarter of a length or shape, they should be able to reconstruct the whole.
Similarly, given two red cubes and being told that the cubes are one-fifth of a stack,
students can make the whole stack.
Understanding the relationship between fractions, as numbers, and the number one is
critical for further learning. Ensure that the students know that a whole, as referred to
in fraction work, means the same as the number one.
Using Materials
Problem: “Four people are at Carla’s birthday, so they will get one quarter
(one-fourth) of the cake each. Carla has 16 candles to put on the cake so that each
person gets the same number of candles on their piece of cake. How many candles
will each person get on their piece of cake?”
Give the students 16 counters and a paper circle to fold into quarters.
Ask, “How many candles do you think each person will get?” “How do you know?”
Look for the students to use adding-related strategies, such as halving and halving
again, like “Eight and eight is 16, so one-half of the cake has eight candles. Four and
four is eight, so one-quarter has four candles.”
Confirm the answers by equally sharing the counters onto the paper circle. There is noneed to do this if the students are able to use partitioning strategies.
Pose similar problems like:
“Five people are at the party. There are 25 candles.”
“Three people are at the party. There are 21 candles.”
Record the answers using symbols, for example, 1/5of 25 is 5.
Vary the problems by using non-unit fractions, like, “At the party the cake is cut into
quarters (fourths). Twelve candles are put on the cake.
Greedy Greg eats three-quarters of the cake. How many candles does he get?” Recordthe results using symbols, that is, 3/4 of 12 is 9.
Using Imaging
Problem: (Show the students one-fifth of a paper circle with four counters on it.)
“Here is a piece of Rongopai’s birthday cake. Each piece of cake has the same
number of candles. How old is Rongopai?”
Reconstructing: Listen to the students’ ideas about how many candles were on the whole cake. Fifths have been deliberately chosen because they are easily confused with quarters. Ask the students to justify their answers.
“I think the cake was cut into five pieces.”
“What would each piece be called?” (one-fifth)
“If there are five pieces, then there are 4 + 4 + 4 + 4 + 4 candles on it.
That’s 20.”
“How did you work out that was 20?”
The whole cake can be constructed, if necessary, to confirm the answers.
Record the answer as: 1/5 of ? is 4, so ? is 20. This means that Rongopai is 20 years
old.
Pose similar problems and ask the students to work out the number of
candles on the whole cake.
1/3 of ? is 6
3/4 of ? is 9
3/5 of ? is 6
Using Number Properties
Ask similar word problems and record them using symbols.
For example:
“Two-thirds of the cake has eight candles on it. How many candles are on the whole
cake?” 2/3 of ? is 8, so ? is 12.
“Three-quarters of the cake has nine candles on it. How many candles are on the
whole cake?” 3/4 of ? is 9, so ? is 12.
Independent Work
Fraction Benchmarks
In this unit students develop important reference points or benchmarks for zero, one half and one. They use these benchmarks to help compare the relative sizes of fractions, through estimating, ordering and placing fractions on a number line.
This unit builds on the following key conceptual understandings about fractional parts.
An understanding of fractional parts supports students to develop a sense for the size of fractions. This unit helps students develop an intuitive feel for zero, one-half and one, as useful benchmarks for ordering fractions. Understanding why a fraction is close to zero, one half or one helps students develop a number sense for fractions.
Students can be supported through the learning opportunities in this unit by differentiating the complexity of the tasks, and by adapting the contexts. Ways to support students include:
The contexts for this unit are purely mathematical but can be adapted to suit the interests and cultural backgrounds of your students. Fractions can be applied to a wide variety of problem contexts, including making and sharing food, constructing items, travelling distances, working with money, and sharing earnings. The concept of equal shares and measures is common in collaborative settings. Students might also appreciate challenges introduced through competitive games or through stories.
Session 1
In this session students begin to develop benchmarks for zero, half and one.
1/20, 6/10, 10/8, 11/12, 1/10, 3/8, 2/5, 9/10.
As the difficulty of this task depends on the fractions, begin with fractions that are clearly close to zero, half or one.
Why do you think 6/10 is close to half? How much more than a half is it? Why do you think 1/20 is close to zero? How much more than zero? Why is 11/12 close to one? Is it more or less than one? How much less?
3/10, 5/6, 5/9, 4/9, 18/20, 13/20, 2/8, 9/12, 1/5
Once more encourage the students to explain their decision for each fraction.
Session 2
In this session the students continue to develop their sense of the size of fractions in relation to the benchmarks of zero, half and one by coming up with fractions rather than sorting them.
5/6
How do you know that fraction is close to one?
5/6 7/8
How do you know that 7/8 is closer to one than 5/6?
Students might comment on how much needs to be added to each fraction to make it equal to one. "7/8 is closer to one because eighths are smaller parts than sixths and 7/8 is 1/8 smaller than 1 and 5/6 is 1/6 smaller than one. As 1/8 is smaller than 1/6, 7/8 is closer to one."
Do you notice a pattern as the fraction gets closer to one? (5/6, 7/8, 9/10, 11/12)
Which fraction is closer to one 99/100 or 999/1000? Why?
Which of these fractions is closest to zero, 1/3, 1/4, 1/5, or 1/6? Explain why?
Can a fraction have 5 as a numerator but still be close to zero? Give an example.
Session 3
In this session students estimate the size of fractions.
Ask for volunteers to record their estimate on the board. As they record estimates, ask each student to share their reasoning. Listen, without judgement to the estimate and then discuss why any given estimate might be a good one. Encourage students to share their justifications and ask questions of each other. There is no single correct answer but the estimates need to be reasonable. If the students are having difficulty, encourage them to reflect on the benchmarks developed in the previous sessions. Look for creative methods like estimating that the white area combines to 1/4 so the shaded area must be 3/4
Session 4
In this activity students identify which fraction of a pair is larger. The comparisons rely on an understanding of the top and bottom number (numerator and denominator) in fractions and on the relative sizes of the fractional parts. Equivalent fractions are not directly introduced in this unit but if they are mentioned by students they should be discussed.
2/5 or 2/8
Encourage explanations that show that the students understand that the fractions have the same number of parts but that the parts are different sizes. In this example 2/8 is smaller than 2/5 because eighths are smaller than fifths. Some students may know that 2/8 = 1/4. Use Fraction Strips to check students predictions.
4/5 or 4/6.
Encourage explanations that show that the students understand that both these fractions have the same count (numerator) but fifths are larger than sixths. Therefore 4/5 is greater than 4/6. Write 4/5 > 4/6. Use Fraction Strips to check students' predictions.
In this example the students can draw on their understanding of the benchmark of 1 and notice that 10/9 is larger than 1 and 9/10 is smaller than 1.
7/10 or 6/10
6/8 or 6/12
3/8 or 4/10 (more difficult)
9/8 or 4/3 etc
One fraction is greater than the other.
The two fractions have different numerators and different denominators.
What might the fractions be?
Session 5
In this session the students draw on their conceptual understanding of fraction benchmarks (0, 1/2, 1) and their understanding of the relative sizes of fractional parts to line fractions up on a number line.
Dear family and whānau,
This week we are learning about where fractions live on number lines. We have been especially interested in fractions that are close to zero, close to one half and close to one. Ask your child to put the following fractions on a number line and explain to you how they made up their mind about where to place them.
1/30 2/99 44/85 99/100 25/60 3/25 77/80 26/50
Worm Wipe-out
This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (442 KB)
use linear proportions to solve problems
Number Framework Links
Use this activity to:
• help the students who are beginning to use advanced additive strategies (stage 6) to become confident at this stage in all three operational domains (addition and subtraction, multiplication and division, and proportions and ratios).
• encourage transition from advanced additive strategies (stage 6) to advanced multiplicative strategies (stage 7)
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book One, Worm Wipe-out, pages 10-11
A classmate
In this activity, the students can use a variety of strategies for simple ratio and proportion problems, ranging from advanced counting approaches to early proportional thinking. They will also consolidate their understanding of simple mixed fractions.
This activity should be introduced through guided teaching rather than as an independent activity unless students are confident at stage 7 or above on the Number Framework.
Begin with some mental exercises to check that the students understand how to find quarters and halves in mixed fractions and equivalences between halves and quarters. For example: How many quarters are in 3/4? How many halves are in 1 1/2 ? So how many quarters are in 1 1/2? You should also check that the students understand that fractions can equally well be expressed as decimals. They may use both in this activity.
Introduce the context using the vet’s instructions. The students could act out this initial situation using large paper circles folded or marked in quarters to model the tablets. Have them mark each quarter of the cat’s tablet as 1 kilogram. This is a good opportunity to introduce the students to the concept of “rate” as a multiplicative relationship between two or more different measurement
units. Here it is tablets per kilogram, but another common example is kilometres per hour, as in 60 km/h.
Send the students to their small groups to work out how many kilograms they need to link to each quarter of the dog’s tablet. Have the students report back on their strategies. If they cannot solve this, give each group 10 rectangular labels of the same size labelled “1 kg of dog”. Have them share these out onto the quarters of one of the dogs’ tablets and insist that they assign all 10 equally to the quarter tablets.
Use the diagram below and ask: How do we share these 2 kilograms among 4 quarters?
Send the students back to their groups to attempt question 1 and then report back on their strategies. Encourage a number of strategies, for example: “I counted the kilograms on each quarter” or “I divided the total cat kilograms by 4 because 4 kilograms makes 1 tablet, and I divided the dog kilograms by 10 and then looked at the remainder.” Rocky’s mass doesn’t fit neatly into the 1/4 tablet rate, so his dosage has to be rounded up.
Question 2 extends the problem by adding the relationship of cost. This involves using two different rates simultaneously, the rate of mass to dose and the rate of tablets to cost. Send the students into their groups with the question: What will you need to know to work out the cost of 1 dose? When they realise that it depends on the number of tablets, they should attempt questions 2a and 2b and report back on their strategies.
For question 3, ask the students: What will you need to know to work out the mass of Brock the dog? After the students have responded, sketch the complete set of relationships used in this problem (using multiples of 1/4 of a tablet):
In question 4, you may need to show the students how to record their trials systematically so that they can use each result as a hint until they find the best result.
Before the students attempt question 5, have them record the cost of each fraction of a tablet for a dog and a cat, for example:
They can use this information to help them make a table (as in question 4) or set up a double number line. For example:
Extension
The students may be able to see that the 35 in $3.50 is the lowest common multiple of 7 x 5. You could also ask them why the answers for questions 3 and 4 are approximate. The reason is that the cat mass doesn’t go up in 1 kilogram steps to match the tablets. A cat weighing 1.1 kilograms would also get tablet. This also introduces the concepts of limits of accuracy and rounding, which is also needed for question 1c.
Answers to Activity
1. a. 1 1/2 tablets
b. 2 1/2 tablets
c. 2 tablets. (Rocky needs 1 4/5 tablets, so 1 3/4 won’t be quite enough.)
2. a. $3.50. ($2 + 3/4 of $2)
b. $15.60. (2 x 1 + 2.80 x 2 + 2.80 x 2
= 3 + 7 + 5.60
= $15.60)
3. More than 5 kg and less than or equal to 7 1/2 kg. (It costs $1.40 per tablet for 5 kg, and 70c per tablet for 2.5 kg. $1.40 + 70c = $2.10)
4. a. Approximately 6 kg (cat) and 15 kg (dog)
b. One strategy is to draw up a table and use trial and improvement. For example:
5. a. The most likely answer is: cat 7 kg and dog 12.5 kg.
b. Strategies will vary. You might use a table, increasing the cost in both the cat and dog columns:
Kapa Haka Practice
This is a level 3 number activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
Click on the image to enlarge it. Click again to close. Download PDF (170 KB)
find fractions of a number
Number Framework Links
Use this activity to:
• help the students who are beginning to use early additive strategies (stage 5) to become confident at this stage in all three operational domains (addition and subtraction, multiplication and division, and proportions and ratios)
• encourage transition from early additive strategies (stage 5) to advanced additive strategies (stage 6)
• help your students to consolidate their knowledge of ordering unit fractions and simple equivalences (fractional numbers, stages 5 and 7).
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book One, Kapa Haka Practice, page 17
A classmate
This activity creates a context in which students work out fractions of a set. They can use a range of strategies in the process, including repeated halving, equal sharing, and using known addition and multiplication facts.
Introduce this activity through a guided teaching group rather than as an independent activity unless your students have strategies at stage 6 or above on the Number Framework. Begin with some mental exercises to practise finding 1/2 and 1/4 of a set, for example, 1/2 of 10, 20, and 30 and 1/4 of 8, 16, and 24.
The students who need to use materials can use the hexagon in a set of international pattern blocks to model the whole group. The trapezium will then represent the 1/2 (the poi), whereas the rhombus will be the using 1/3 rakau. Complete the hexagon with a triangle and ask the students: How much of the whole hexagon is the triangle? When they can see that it represents 1/6 of the whole, make sure that they identify the 1/6 with the rest of the students who will be in the group practising waiata.
When the students understand that 1/6 of the group will practise waiata, check that they understand the connections between the numbers of students and the number of poi, ràkau, and waiata sheets mentioned in the problem.
Send the students into small groups to attempt question 1. They should report back before doing question 2. Some students may need to sketch a large hexagon showing the division into 1/2, 1/3, and 1/6. They could use 60 beans or counters to represent the team members and model the solution by sharing out the beans over the hexagon. Encourage the students to use number properties to anticipate the result of equal sharing before they use materials.
The students who use number properties to find 1/3 of the set will either divide by 3 or change the question to 3 x = 60 and ask themselves: “What is the value of the box?”
In question 2, have the students look for an easy way to solve the problem. If necessary, prompt them to use question 1 to help them work out question 2. Note that the number of waiata sheets should be rounded up to the nearest whole number to be sensible.
Question 3 will be more of a challenge. Remind the students that if 204 is too hard to work with, they can split it into easy parts. Send them into groups to find some good splits and report back on these. They may see that 204 = 60 + 60 + 60 + 24, so they only have to work out what share the 24 get because they know what 60 members get from question 1. Similarly, 204 = 180 + 24, so they could use twice the answer for question 2 plus the shares for the extra 24.
Answers to Activity
4. Strategies will vary. First you need to find the number of students in each group. You could use a box diagram to help you. This example uses the 60 students from question 1:
Or you could divide 60 by 2 and 3. Once you have the numbers in each group, you can double or divide by 2 to find out how much equipment is needed. For the 90 students, you could use 1 times the 60-student numbers.
Pet Boasting
This is a level 2 number activity from the Figure It Out series. It relates to Stage 5 of the Number Framework.
Click on the image to enlarge it. Click again to close. Download PDF (170 KB)
Find fractions of a number
Use a variety of operations to solve problems
Number Framework Links
Use these activities to:
• encourage transition from advanced counting strategies (stage 4) to early additive strategies (stage 5)
• help the students who are beginning to use early additive strategies (stage 5) to become confident at this stage in all three operational domains (addition and subtraction, multiplication and division, and proportions and ratios)
• help your students to consolidate and apply their knowledge of basic multiplication facts.
These activities expose students to a range of strategies, from simple addition to multiplication and division with single-digit factors and multiplication using simple unit fractions. To do these activities, the students need a basic understanding of multiplication and a knowledge of simple unit fractions.
Activity One
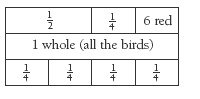
Question 2 challenges students to understand the relationship between halves, quarters, and the whole as a set.
If you are using materials and images, fraction pieces such as those in the Numeracy Project Material Master 4-19 (see Related Resources) or commercial fraction
pieces will be useful. Ask the students: How can we use this model or diagram to find the total number of birds?
Extension
As an extension using number properties, have the students record equations showing how many of each type of bird there are, that is, 1/2 x 24 = 12 blue birds and 1/4 x 24 = 6 yellow.
Ask them: What happens to a set if you multiply it by a half or a quarter? The students should notice that multiplying by a fraction makes the number smaller. Try to generalise this observation by exploring multiplying by fractions less than 1 and then by fractions greater than 1. This will help the students gain the critical understanding that multiplying by 1 is the point at which the quantity remains constant.
Activity Two
If you are using this activity for guided teaching, encourage the students to first make sure that they understand the problem. They must be able to find the relationships that connect the clues presented by the characters. Use small groups (discussed in the notes for “Wrapping up Wontons”) and have them present a report with diagrams that explain these connections. The students could then return to their groups to attempt the problems and report back on their strategies.
If you think materials will help the students, you could encourage the groups to act out the characters and use counters or beans to represent their pet. Animal strips like those in the Numeracy Project Material Master 5-2 could also be used or adapted to help solve the problems.
Answers to Activities
Activity One
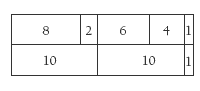
1. 21. (Using a “make tens” strategy, this is 8 + 2 + 6 + 4 + 1.)
2. 24. ( 1/2 + 1/4 = 3/4 , so are red. 6 are red, so 6 are yellow and 12 are blue. 6 + 6 + 12 = 24)
Activity Two
1. 108
2. Strategies may vary. A possible strategy is:
Harry has 3 goats. Tanya has 3 x 3 or 3 + 3 + 3 = 9 pigs.
Mari has 9 x 2 or 9 + 9 = 18 lambs.
Losi has 18 ÷ 3 = 6 calves (3 x ? = 18).
3 + 9 + 18 + 6 = 36. (You could use a tens strategy here:
2 + 10 + 20 + 4 = 10 + 20 + 6
= 36.)
Sonya has 2 x 36 or 36 + 36 = 72 rabbits (30 + 30 = 60, 6 + 6 = 12, 60 + 12 = 72). The total number of pets is therefore 36 + 72 = 108. On a number line, the
addition could be shown like this:
3. Problems and strategies will vary.
Material Masters Fraction Pieces 4-19, Animal Strips 5-2
DVD Decisions
This is a level 3 number activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
Click on the image to enlarge it. Click again to close. Download PDF (170 KB)
find fractions of money amounts
Number Framework Links
Use this activity and investigation to:
• help the students who are beginning to use early additive strategies (stage 5) to become confident at this stage in all three operational domains (addition and subtraction, multiplication and division, and proportions and ratios)
• encourage transition from early additive strategies (stage 5) to advanced additive strategies (stage 6).
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book One, DVD Decisions, page 12
A classmate
By combining the money context with different numbers of friends sharing costs, this activity allows a variety of strategies to be used with subtraction, division, and fractions.
The students at stage 6 (advanced additive) or above could attempt this activity independently in groups and report back.
Introduce this activity to a guided teaching group by pointing out that the DVD prices have been rounded up to a tidy dollar amount even though shops almost always price them at so many dollars and 95 cents. This rounding enables the students to calculate the shared costs better because we cannot split 5 cents in real money.
Introduce or revise , , and of $1.00 as 25 cents, 50 cents, and 75 cents respectively. These facts will be useful in solving some problems. The students could record these with other facts that they need to memorise.
The students who need to use materials could act out the scenarios in each question with play money and a card representing each DVD. When they report back, discuss different ways to split the cost equally. Ideas may include sharing out dollars in units of $1, $5, or $10 notes, one at a time, and then sharing out coins in the same way, as needed, to meet the price.
For imaging, have the students pretend that their money is being carried by an adult and that they have to ask for the notes and coins they will use to buy each DVD. They receive the money after they have solved the sharing problem by imaging the money they need.
To encourage the students to use number properties, put them in small groups and ask them to find and share different ways of using and recording numbers and operations to solve the problems.
Highlight the connections between ideas. For example, question 1 can be solved by having the three friends sharing out $5, $5, and $5, then $2, $2, and $2, and finally, $2, $2, and $2 again while they keep a running total. The students who know x 3 = 27 should see that this is the same as sharing out $9, $9, and $9.
Question 1b provides an opportunity to discuss and reinforce the connection between $27 ÷ 4 and finding 1/4 of $27. Students don’t automatically understand that dividing by a number and multiplying by its inverse (reciprocal) are just two different ways of viewing the same thing. (Dividing by 4 is accessible to early additive students if they use halving and halving.)
When students see that dividing by 4 has the same effect as multiplying by and vice versa, create a pattern by extending this to dividing by 2 and multiplying by and other pairs of reciprocals, such as 1/3 and 3. Encourage the students to describe the pattern.
Investigation
Remind the students before they begin the investigation to round the cost of the DVDs to the nearest whole dollar
Answers to Activity
1. a. $9
b. i. $6.75. Methods will vary. Continuing Kinesha’s thinking, you could say $3 is
the same as $4 – (4 x 25c), so of the $3, each person pays $1 – 25c or 75c.
$5 + $1 + 75c = $6.75
ii. Strategies will vary. For example:
$28 ÷ 4 = $7, and $1 ÷ 4 = 25c. $27 = $28 – $1, so 1/4 of $27 is $7 – 0.25c, which is $6.75
Another strategy is 8 + 8 + 8 + 3 = 28. 1/4 of each of these bits is
2 + 2 + 2 + 0.75 = 6.75
2. $27.50. One way to work this out is:
30 + 25 = $55. 55 ÷ 2 = $27.50. Another way is to work out of 30 + of 25.
15 + 12.50 = $27.50
3. $24. (32 ÷ 4 = 8. 32 – 8 = 24 or 30 – 10 + 4 = 24)
4. a. $9. (39 – 30)
b. Answers will vary. For example, she could pay for 1/2 of Making Masks with 1 other. If Alana doesn’t mind paying more than the others, she could pay $9 towards a video, and her friends could share the rest. For example, she could pay $9 towards Smash Hits, and 2 of the others could pay $8 each (9 + 8 + 8 = $25).
Investigation
Results will vary.
Birthday cakes
Find fractions of a set using multiplication and division.
Number Framework Stage 6
Paper circles (to represent cakes)
Background Maths
Fractions involve a significant mental jump for the students because units of one,which are the basis of whole-number counting, need to be split up (partitioned) andrepackaged (re-unitised). It is crucial that the students have significant opportunitiesto split up ones through forming unit fractions with materials and are required torecombine several of these new units to form fractions like two-thirds and five quarters.
Using Materials
Using Imaging
Problem: (Show the students one-fifth of a paper circle with four counters on it.)
Reconstructing: Listen to the students’ ideas about how many candles were on the whole cake. Fifths have been deliberately chosen because they are easily confused with quarters. Ask the students to justify their answers.
“I think the cake was cut into five pieces.”
Using Number Properties
Ask similar word problems and record them using symbols.
Independent Work
Fraction Benchmarks
In this unit students develop important reference points or benchmarks for zero, one half and one. They use these benchmarks to help compare the relative sizes of fractions, through estimating, ordering and placing fractions on a number line.
This unit builds on the following key conceptual understandings about fractional parts.
An understanding of fractional parts supports students to develop a sense for the size of fractions. This unit helps students develop an intuitive feel for zero, one-half and one, as useful benchmarks for ordering fractions. Understanding why a fraction is close to zero, one half or one helps students develop a number sense for fractions.
Students can be supported through the learning opportunities in this unit by differentiating the complexity of the tasks, and by adapting the contexts. Ways to support students include:
The contexts for this unit are purely mathematical but can be adapted to suit the interests and cultural backgrounds of your students. Fractions can be applied to a wide variety of problem contexts, including making and sharing food, constructing items, travelling distances, working with money, and sharing earnings. The concept of equal shares and measures is common in collaborative settings. Students might also appreciate challenges introduced through competitive games or through stories.
Session 1
In this session students begin to develop benchmarks for zero, half and one.
1/20, 6/10, 10/8, 11/12, 1/10, 3/8, 2/5, 9/10.
As the difficulty of this task depends on the fractions, begin with fractions that are clearly close to zero, half or one.
Why do you think 6/10 is close to half? How much more than a half is it? Why do you think 1/20 is close to zero? How much more than zero? Why is 11/12 close to one? Is it more or less than one? How much less?
3/10, 5/6, 5/9, 4/9, 18/20, 13/20, 2/8, 9/12, 1/5
Once more encourage the students to explain their decision for each fraction.
Session 2
In this session the students continue to develop their sense of the size of fractions in relation to the benchmarks of zero, half and one by coming up with fractions rather than sorting them.
5/6
How do you know that fraction is close to one?
5/6 7/8
How do you know that 7/8 is closer to one than 5/6?
Students might comment on how much needs to be added to each fraction to make it equal to one. "7/8 is closer to one because eighths are smaller parts than sixths and 7/8 is 1/8 smaller than 1 and 5/6 is 1/6 smaller than one. As 1/8 is smaller than 1/6, 7/8 is closer to one."
Do you notice a pattern as the fraction gets closer to one? (5/6, 7/8, 9/10, 11/12)
Which fraction is closer to one 99/100 or 999/1000? Why?
Which of these fractions is closest to zero, 1/3, 1/4, 1/5, or 1/6? Explain why?
Can a fraction have 5 as a numerator but still be close to zero? Give an example.
Session 3
In this session students estimate the size of fractions.
Ask for volunteers to record their estimate on the board. As they record estimates, ask each student to share their reasoning. Listen, without judgement to the estimate and then discuss why any given estimate might be a good one. Encourage students to share their justifications and ask questions of each other. There is no single correct answer but the estimates need to be reasonable. If the students are having difficulty, encourage them to reflect on the benchmarks developed in the previous sessions. Look for creative methods like estimating that the white area combines to 1/4 so the shaded area must be 3/4
Session 4
In this activity students identify which fraction of a pair is larger. The comparisons rely on an understanding of the top and bottom number (numerator and denominator) in fractions and on the relative sizes of the fractional parts. Equivalent fractions are not directly introduced in this unit but if they are mentioned by students they should be discussed.
2/5 or 2/8
Encourage explanations that show that the students understand that the fractions have the same number of parts but that the parts are different sizes. In this example 2/8 is smaller than 2/5 because eighths are smaller than fifths. Some students may know that 2/8 = 1/4. Use Fraction Strips to check students predictions.
4/5 or 4/6.
Encourage explanations that show that the students understand that both these fractions have the same count (numerator) but fifths are larger than sixths. Therefore 4/5 is greater than 4/6. Write 4/5 > 4/6. Use Fraction Strips to check students' predictions.
In this example the students can draw on their understanding of the benchmark of 1 and notice that 10/9 is larger than 1 and 9/10 is smaller than 1.
7/10 or 6/10
6/8 or 6/12
3/8 or 4/10 (more difficult)
9/8 or 4/3 etc
One fraction is greater than the other.
The two fractions have different numerators and different denominators.
What might the fractions be?
Session 5
In this session the students draw on their conceptual understanding of fraction benchmarks (0, 1/2, 1) and their understanding of the relative sizes of fractional parts to line fractions up on a number line.
Dear family and whānau,
This week we are learning about where fractions live on number lines. We have been especially interested in fractions that are close to zero, close to one half and close to one. Ask your child to put the following fractions on a number line and explain to you how they made up their mind about where to place them.
1/30 2/99 44/85 99/100 25/60 3/25 77/80 26/50
Getting partial
In this unit we explore fractions of regions as well as fractions of sets. We look for, and develop understanding of, the connection between fractions and division.
Fractions are one of the first departures from whole numbers that students will see. This unit introduces a number of important concepts relating to fractions. The first of these is that fractions represent parts of one whole, and can be represented in a variety of ways including regions and sets. This makes them useful in a large variety of situations where whole numbers by themselves are inadequate.
The second useful concept is that a given number can be represented as a fraction in many ways. Knowing that fractions such as ½ can be disguised as 2/4 or 3/6, etc is important both for recognition purposes and for use in calculations.
Finally, students should know that fractions can be represented both as one whole number divided by another whole number and as points on the number line. Having a knowledge of the different representations of fractions provides connections across mathematics for students and so increases their level of understanding.
In this unit we also introduce the idea of a fraction of 100. This lays the groundwork for the decimal representation of fractions at Level 3, and percentages at Level 4. These ideas are developed further in the units Getting the Point, Level 3 and Getting Percentible, Level 4. Facility with fractions is also an important precursor for algebra. Algebraic fractions have a wide range of uses. Without a good understanding of how fractions work, students will be restricted in their work at higher levels when fractions occur in algebraic settings.
This unit can be differentiated by varying the scaffolding provided or altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
The context for this unit can be adapted to recognise diversity and student interests to encourage engagement. Consider making links between the learning in these sessions and relevant learning from other curriculum areas (e.g. number of children competing in different events at the School Athletics championship, numbers of different native birds observed in a week). For example:
Te reo Māori vocabulary terms such as hautau (fraction), haurua (half), hauwhā (quarter), haurima (fifth), hauwaru (eighth) and hautekau (tenth) as well as numbers in Māori could be introduced in this unit and used throughout other mathematical learning.
Session 1
Here we look at different representations of 1/2.
Session 2
Here we look at fractions other than 1/2 and consider ways to represent these fractions that involve 100.
Session 3
This session involves fractions in problem situations.
Session 4
Another way to represent numbers is the number line. Here we use the number line to show the relative positions and sizes of fractions.
These problems will highlight students’ knowledge of the relative size of fractions. For example, a student might find half of the distance between 0 and 1/5 to see where 1/10 should be or half the distance between 1/2 and 1 to see the location of 3/4 . The problems will also highlight their understanding of the role of the numerator (top number) as the selector of the number of parts and the role of the denominator (bottom number) as nominating how many equal parts the whole is separated into.
Session 5
Here we try to link the concepts of fractions in length and sets by dividing up a big worm.
The worm was 18 cubes long. Each bird got three cubes of worm. How many birds were there?
Dear family and whānau,
This week we have been thinking about fractions. Ask your child to explore some fractions with you. For example: take a newspaper or magazine and ask them to find the longest word that they can. How many letters does it have? Now find some words that are half that length or a third of the length or a quarter of that length. Ask your child to record the words they find and the fractions you talk about.
How many pages does the paper or magazine have? What is half that number and a quarter of that number?
We would be glad if the answers could be brought back to class so that we can discuss them.
Figure it Out Links
Some links from the Figure It Out series which you may find useful are:
Equivalent Fractions
In this unit we are exploring ways to find equivalent fractions. We use the concept of equivalent fractions to convert fractions to the benchmark fractions of halves, quarters, thirds, fifths and tenths. From these benchmark fractions it is easier to convert fractions to decimals and percentages. We use equivalent fractions to compare fractions.
Fractions are an extension of whole numbers and integers. Fractions are needed when wholes (ones) are not adequate for a task. Division often requires equal partitioning of ones. Sharing two chocolate bars equally among five people requires that the bars be cut into smaller equal parts. The operation might be recorded as 2 ÷ 5 = 2/5. Note that the number two fifths, is composed of two units of one fifth. In practical terms the equal share can occur by dividing each of the two bars into fifths, then giving each person one fifth from each bar.
If the bar was made up of ten pieces then each person might be given two tenths from each bar, giving them four tenths in total. Four tenths are the same quantity of chocolate as two fifths. Any fraction can be expressed as an infinite number of equivalent fractions that represent the same quantity and occupy the same position on the number line.
Fractions are important to measurement, especially where whole units are not precise enough for the purpose. The symbolic expression does not explain why equivalent fractions represent the same amount. Consider these equivalent fractions: 2/3 = 4/6 = 8/12 . A fraction strip (length) model of the relationships looks like this:
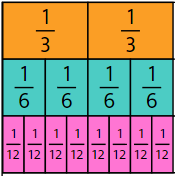
Sixths are half the size of thirds so twice as many sixths fit into the same length as thirds.
Twelfths are quarter the size of thirds so four times as many twelfths fit into the same length as thirds.
The relationship between two thirds and eight twelfths can be represented in this equality.
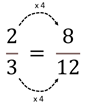
Four times as many twelfths comprise one as thirds. Therefore, each third can be divided into four twelfths.
Understanding equivalent fractions is critical to making sense of decimals and percentages. Consider the names for 3/4 = 0.75 = 75%. Both 0.75 and 75% represent 75/100 which is an equivalent fraction to 3/4. If each quarter is equally partitioned into 25 parts, those parts are called hundredths since 4 x 25 of those parts fit into one.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
Adaptation involves changing the contexts used for problems to meet the interests and cultural backgrounds of your students. Where contexts such as food and ratios of orcas and dolphins may not be appropriate for your students, find other situations likely to engage them. Birthday cakes might be replaced by areas of land, dart boards, or gold coins. Orcas and dolphins might be replaced by other animals that need conservation. Linear models are easily applied to journeys that students make, or physical objects such as tape and rope.
Te reo Māori vocabulary terms such as hautau (fraction), hautau ōrite (equivalent fraction), rārangi tau (number line), and haurua, hautoru, hauwhā, haurima… (half, third, quarter, fifth…) could be introduced in this unit and used throughout other mathematical learning.
Session One
How do we read these fractions? (two thirds and three quarters)
What picture do you see when you think …about two-thirds? ...about three quarters?
Invite individual students to draw representations of the fractions.
Main points to bring out are:
Nia and Ashanti are identical twins.
Each birthday they each get identical birthday cakes.
Nia eats two thirds of her cake and Ashanti eats three quarters of her cake.
Who eats the most?
How much more cake does she eat than her sister?
What fraction of the whole cake is each piece? (twelfths – Why?)
How many twelfths are shaded?
Two thirds equals how many twelfths?
What fraction of the whole cake is each piece? (twelfths – Why?)
How many twelfths are shaded?
Three quarters equals how many twelfths?
How much greater is three quarters than two thirds? (one twelfth)
You might record 3/4 > 2/3 because 9/12 > 8/12 and ask students to explain the meaning of the symbols.
The Po and Mangu story compares 3/5 and 5/8. Students should realise that both fifths and eighths can be equi-partitioned into fortieths.
3/5 = 24/40 and 5/8 = 25/40 so 5/8 is 1/40 greater than 3/5. Some students might use division on a calculator to check the comparison. 3/5 = 0.6 and 5/8 = 0.625. This means of comparison might open up a conversation about fractions as decimals.
The Thalia and Andreas story compares 2/3 and 7/10. Both thirds and tenths can be equi-partitioned into thirtieths. 2/3 = 20/30 and 7/10 = 21/30 so 7/10 is greater by 1/20. The decimal conversions are 2/3 = 0.6666... and 7/10 = 0.7.
Session Two
When we say that two or more fractions are equivalent, what do we mean?
Do you know any pairs of equivalent fractions already?
What patterns are true for all three pairs?
Students might notice that there is always an equals sign. What does that symbol mean?
Some might notice that the numerators and denominators are multiplied by the same number, e.g. by four in the pair 2/3 = 8/12.
What does the multiplication mean? In the example, four times as many twelfths fit in one as thirds, so four times as many twelfths fit into the same space as two thirds.
Three goats share two hay bales equally. Each goat gets the same amount.
Six sheep share four hay bales equally.
How could we record the problem using a diagram? (Students often draw lines connecting animals and bales)
How could we record the problem using symbols? Sharing can be represented by division; 2 ÷ 3 = 2/3 (goats) and 4 ÷ 6 = 4/6 (sheep). Do your students recognise that two thirds of a bale is equivalent to four sixths of a bale? The shares are equal since 2/3 = 4/6.
Work through each problem with your students. Let them attempt the problem first before sharing strategies.
Students may get confused by which number is the divisor in the kiore and heihei problem. Three kiore sharing four kumara should be represented as 4 ÷ 3 = 4/3 = 1 1/3.
Nine heihei sharing 12 kumara should be represented as 12 ÷ 9 = 12/9 = 1 3/9.
Since 1/3 = 3/9 the shares are equal.
Shares for the kotare and kiwi are as follows:
4 ÷ 5 = 4/5 (kotare) and 9 ÷ 10 = 9/10 (kiwi)
A qualitative judgement is needed to establish that kiwi get more worms each.
4/5 = 8/10 so kiwis get 1/10 of a worm more than kotare.
The shares are equal.
The shares are equal.
Albatrosses get more, 1/10 of an oyster more.
Goats get more, 7/36 of a bale more.
4/5 = 16/20 = 20/25 = 24/30 etc.
5/8 = 10/16 = 15/24 etc.
Session Three
Where does the number one half live on the number line?
Be aware that some students may think you mean one half of the whole line, i.e. one half of 3 or 1 ½. This common issue is about confusing 1/2 as an operator with 1/2 as a number.
How can we locate one half exactly?
Three halves (3/2) three quarters (3/4) five quarters (5/4) ten quarters (10/4)
Five eighths (5/8) eleven eighths (11/8) two thirds (2/3) seven thirds (7/3)
You will get a set of cards (Copymaster 3: Set One).
Your job is to draw a line and organise the cards in order along the line.
Students might use a large sheet of paper and glue stick to create their number lines in pairs.
Add these extra fractions to your number line.
Look for students to:
Which fractions are the hardest to locate? Why?
Is there a way to simplify those fractions so the task is easier?
I am a fraction.
I am between two thirds and three quarters.
My denominator is 24.
Who am I?
Session Four
Use PowerPoint 3 to introduce the context of orca and dolphin numbers. Slide Three shows these data:
What do you notice about the data?
Students might comment that the numbers of creatures is much less in July compared to January. Why?
Compared to January, what fraction of the total number of creatures were in July?
12/24 = 1/2 so there are half as many creatures in July.
Are the fractions the same for both months?
8/24 (8 out of 24 for orcas) and 16/24 (16 out of 24 for dolphins) in January
3/12 (3 out of 12 for orcas) and 9/12 (9 out of12 for dolphins) in July
Can we simplify these fractions to make them easier to compare?
8/24 = 1/3 and 16/24 = 2/3
3/12 = 1/4 and 9/12 = 3/4
The fraction of orcas is slightly less in July than in January. Perhaps orcas prefer cooler water.
What fractions can you see? Explain where you see those fractions.
Draw a diagram to show how the fractions ¼ and ¾ can be seen in the orca and dolphin data.
Let students draw their own diagram before animating the slide.
Which month has the greatest fraction of orcas in the whole group?
Do students recognise that the fraction of orcas equals three fifths for both months?
Answers
Kawhia Harbour
January July
Fraction of orcas = 1/2 Fraction of orcas = 1/2
Fraction of dolphins = 1/2 Fraction of dolphins =1/2
Is there a change in the fraction for each creature comparing July to January? Same
Whitianga Coast
January July
Fraction of orcas = 10/25 = 2/5 Fraction of orcas = 4/10 = 2/5
Fraction of dolphins = 15/24 = 3/5 Fraction of dolphins = 6/10 = 3/5
Is there a change in the fraction for each creature comparing July to January? Same
Queen Charlote Sound
January July
Fraction of orcas = 6/24 = 1/4 Fraction of orcas = 4/16 = 1/4
Fraction of dolphins = 18/24 = 3/4 Fraction of dolphins = 12/16 = 3/4
Is there a change in the fraction for each creature comparing July to January? Same
Kaipara Harbour
January July
Fraction of orcas = 10/20 = 1/2 Fraction of orcas = 4/10 = 2/5
Fraction of dolphins =10/20 = 1/2 Fraction of dolphins = 6/10 = 3/5
Is there a change in the fraction for each creature comparing July to January?
The fraction of dolphins increases and the fraction of orcas decreases.
Akaroa Harbour
January July
Fraction of orcas = 4/24 = 1/6 Fraction of orcas = 2/16 = 1/8
Fraction of dolphins = 20/24 = 5/6 Fraction of dolphins = 14/16 = 7/8
Is there a change in the fraction for each creature comparing July to January?
The fraction of dolphins increases and the fraction of orcas decreases.
Hawke Bay
January July
Fraction of orcas = 12/40 = 3/10 Fraction of orcas = 9/21 = 3/7
Fraction of dolphins = 28/40 = 7/10 Fraction of dolphins = 12/21 = 4/7
Is there a change in the fraction for each creature comparing July to January?
The fraction of orcas increases and the fraction of dolphins decreases.
Session Five
Extension
Dear parents and caregivers,
This week we are learning about equivalent fractions that are different ways to represent the same amount. For example, one half (1/2) of a birthday cake is the same amount as two quarters (2/4) or four eighths (4/8). We can write the equivalence as 1/2 = 2/4 = 4/8.
Ask your student to explain how he or she compares the size of two fractions with different denominators. For example, “Which fraction is greater: 2/3 or 3/4? How much greater?”
Figure It Out
Some other links from the Figure It Out series which you may find useful are:
Getting Percentible
This unit explores the connections between percentages, decimals, and fractions. It focuses on strategies for solving problems involving percentages and applies these strategies to real life contexts.
Percentages are commonly used in real life. Many of these applications involve money. So in this unit students investigate applying percentages to sales, discounts and investments.
This unit provides practice in using percentages in a range of situations and develops the link between percentages, decimals and fractions. Prior to using this unit, students should be familiar with decimals and fractions. The Level 4 units: Getting Partial to Fractions, Getting Partial to Decimals, and Getting Partial: Fractions of sets form a good foundation for the content in this unit. Getting Partial to Percentages is a parallel unit to this one. You may wish to use parts of each.
Percentages are rates out of 100 (per hundred). 50% means at a rate of 50 out of 100, a rate that is equivalent to one half. This means that 50% of a quantity (say, 40) can be calculated by multiplying the quantity by 50/100 (say, 40 x 50/100). The answer, 20, reflects the fact that 50 out of 100 and 20 out of 40 are equivalent rates, just like the fractions 50/100 and 20/40 are equivalent.
50% can be represented as an infinite number of equivalent fractions, such as 50/100 = 1/2 = 2/4 = 23/46, …. Percentages can be written as decimals, using the structure of the place value system. 50/100 also means 50 hundredths which is 5 tenths or 0.5 (note that 5 is in the tenths place). As a decimal, 50% can be represented as 0.5. Converting percentages to decimals can sometimes assist in calculation, such as 0.6 x 80 = 48 is an equivalent calculation to 60% x 80 = 48.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
The contexts for activities can be adapted to suit the interests and experiences of your students by:
Te reo Māori kupu such as ōrau (percent), hautau (fraction), hautaunga ā-ira (decimal fraction), and whakahekenga ōrau (percentage discount) could be introduced in this unit and used throughout other mathematical learning
Pre-prepared spreadsheets and copies for students (for session 5)
Session 1
Today we explore the relationship between percentages and fractions.
You may need to revisit a material model of decimal place values, such as deci-lengths or decimats to show why 50 hundredths equals 5 tenths.
Ask students to predict what fractions and percentages occur if the halving continues.
What is half of one quarter?
What is one eighth as a percentage? (Half of 0.25 equals 0.125 or 12.5%)
Deci-lengths or deci-pipes are useful to show the halving.
Extend the pattern to sixteenths.
1/5, 3/5, 3/2 (1 1/2), 9/4 (2 1/4), 1/10, 1/8
From this table we see that 1/8 = ½ x 25% = 12.5 %.
Students may use any of the previously-introduced strategies to solve these problems.
Session 2
In this session students solve percentage problems using a range of strategies and share those strategies.
Tāmati is trying to work out the number of goals scored by the Northern Mystics in a netball game against the Southern Steel. His sister tells him that the Northern Mystics scored 25% of the goals. The total number of goals scored throughout the game, by both teams, was 48. How many goals did the Northern Mystics score?
Tipene helps his Uncle Kahu check the kōura pots in the boat. He is allowed to keep 20 % of the kōura they catch. One day Tipene and Kahu catch 25 kōura. How many kōura is he allowed to keep?
Jar A: 30 cubes, 50% yellow, 20% green, 30% blue (15 yellow, 6 green, 9 blue)
Jar B: 36 cubes, 25% red, 75% blue (9 red, 27 blue)
Jar C 20 cubes, 20% black, 5% blue, 50% green, 25% yellow (4 black, 1 blue, 10 green, 5 yellow)
Jar D: 16 cubes, 12.5% white, 37.5% red, 50% orange (2 white, 6 red, 8 orange)
Jar E: 60 cubes, 10% yellow, 20% blue, 30% green, 40% red (6 yellow, 12 blue, 18 green, 24 red)
Session 3
In this lesson students use the percentage key on the calculator to solve problems. Encourage your students to justify the reasonableness of the answers that they get.
50% is 1/2, so 50% of 25 is one-half of 25;
25% is 1/4, so 25% of 50 is one-quarter of 50;
Since 50 is twice as much as 25, and one-quarter is half of one-half, the answers must be equal (doubling and halving argument);
50 x 25% gives the same result as 25 x 50% as only the order of the factors is changed. This argument is not strictly correct since 50 x 0.25 is not the same operation as 25 x 0.5.
Hirini gives 40% of his marbles to Melanie. He still has 21 marbles left. How many marbles did he have to start with?
Sione uses 45% of his free call minutes for this month in the first week. He has only 88 minutes left. How many free minutes does he get on his mobile plan each month?
Session 4
In this session students apply their knowledge of percentages to solve shopping problems.
Ask the students which arrow they think matches what you would pay in a 25% off sale. Look for explanations like, "You would pay 75% of the price since 100% - 25%= 75%".
To conclude the session, pose this problem. "Suppose you have $1000. You want to buy as many computer games as you can. Normally they cost $100 each. How many can you buy with no discount, 10% discount, 20% discount, 30% discount, etc? What do you notice about the number of games you can buy as the discount gets greater?" Suggest to the students that they may want to use a table or graph to record their findings.
Students may notice that the impact of discount is not linear. For example, a purchaser gets twice as many of an article at 70% discount as they do at 40% discount.
Session 5
In today’s session we explore the use of percentages through banking problems.
Why is it important to save money?
Is it worth it to save money or should you just spend it?
How does the bank reward you for leaving your money with them?
Students may or may not know about compound interest. You might demonstrate what an interest rate of 10% per annum is like. Put $100 into a container (Material Master 4-9). Each time a year passes, the bank adds 10% or 1/10 of the amount to the account.
After 1 year there is $100 + $10 = $110 in the account.
After 2 years there is $110 + $11 = $121 in the account.
What will happen at the end of Year 3?
After 3 years there is $121 + $12.10 = $133.10 in the account.
What do you notice about the amount as the years go by?
SafeBank will pay you $60 000 each year for all ten years that your money is with them.
RegularBank will pay you 5% compound interest at the end of every year. That means the 5% you earned in the year before will also earn interest.
StepBank will pay you 1% compound interest at the end of the first year, 2% at the end of the second year, 3% at the end of the third year, and so on until they pay 10% at the end of the tenth year.
Which bank will give you the most money at the end of ten years?
Dear family and whānau
In maths this week we have explored the connections between percentages, decimals, and fractions. We have focused on strategies for solving problems involving percentages and applying these strategies to real life contexts.
At home this week we would like your child to find examples of percentages in some form of media (e.g. the newspaper, on TV, in an online advertisement, in a magazine). They should use their knowledge of percentages to make sense of the item. We would like them to write a brief explanation to accompany the item and bring this to class to share.
Figure it out
Some links from the Figure It Out series which you may find useful are:
Adding and subtracting fractions
These exercises and activities are for students to use independently of the teacher to practice number properties.
Add and subtract fractions with like denominators
Identify fractions that equal one
Identify fractions bigger than one
Addition and Subtraction, AA (Stage 6)
Prior knowledge.
Background
Before this activity is commenced, students should have learnt that fractions can be smaller than one, can equal one, and be greater than one, and can relate drawings to numeric fractions. It is also useful if they can convert improper fractions to mixed numbers, though as the students are at stage 5 this is likely to be using additive methods rather than multiplicative ones.
Comments on the Exercises
Exercise 1
Asks students to solve addition problems with fraction with the support of diagrams. Exercise 1 is an exploration that hopes to build on students’ existing knowledge about fractions to help students establish/invent a strategy for adding simple fractions. The first problems have both a word story and a set of drawings to represent the story mathematically. Some students may need to be introduced to the idea that both of these representations show the same thing. The next problems rely simply on the drawings. Once students have developed a strategy for adding such fractions, they are then invited to use this on some numeric fractions
Exercise 2: Parts in a whole
Asks students to revisit the idea that n/n = 1
Exercise 3
Asks students to solve problems involve addition of fractions with like denominators. Many have answers that are greater than one. Students who have learned to convert improper fractions to mixed numbers should be challenged to make this conversion, even though the answers do not provide this format. Likewise, answers are not simplified as students at this stage cannot be expected to understand multiplicative processes.
Investigation
Asks students to think about subtraction of fractions with like denominators, again starting with story problems and drawings that show these. Some students may find it challenging to make up the word problems required, or how this could be represented with drawings. This investigation can form part of a teaching session which covers the same concepts.
Exercise 4
Asks students to solve basic subtraction problems with like denominators
These activities can be used to follow the teaching episodes based on, Book 8, Fractions in a Whole and are for those students who are able to use the associated number properties.
Legs in the barn
This problem solving activity has a number focus.
One third of the animals in the barn are chickens. The rest are pigs.
There are 20 legs in all.
How many pigs are there?
The focus of this problem is on fractional parts of a set. The problem encourages students to approach fraction operations through number sense and logical thinking rather than through the memorisation of rules. Other contexts for this problem could include bicycles, tricycles and a number of wheels, or spiders and bugs, and a number of legs.
The Problem
One third of the animals in the barn are chickens. The rest are pigs. There are 20 legs in all. How many pigs are there?
Teaching Sequence
How do you work out a third?
What is the total number of legs? Will this number be the numerator or denominator of a fraction?
How many thirds make up 1 whole?
How many legs make up our '1 whole'?
Extension
Write your own barn fraction problem which has 6 as the answer.
Solution
4 pigs
One way to do this problem is to use a table. Before we start though, notice that: (1) if one third of the animals are chickens, then two thirds are pigs, and (2) since there are a whole number of chickens, there must be three times a whole number of animals.
Noticing part (2) makes it possible to get the answer very quickly.
Addition, subtraction and equivalent fractions
The purpose of this series of lessons is to develop understanding of equivalent fractions and the operations of addition and subtraction with fractions.
In this unit students learn to find equivalent fractions and apply equivalence when adding and subtracting fractions with different denominators. A fundamental idea about addition and subtraction is that the units that are combined, separated, or compared are of the same size. In a simple addition problem such as 6 + 7 = 13 it is assumed that 6, 7, and 13 refer to the same units, such as apples, or centimetres.
Addition and subtraction of fractions involves greater complexity than with whole numbers.
For example, 3/4 + 2/5 = ? involves two fractions composed of different units. Three quarters refer to three units that are one quarter in size, while two fifths refer to two units that are one fifth in size. Since quarters and fifths are different sized units they cannot be added. Key to this, is understanding that the denominator in a fraction describes the size of units the fraction is made up of.
Renaming the fractions in units of the same size involves creating a common or "like" denominator. A common denominator can be any common multiple of the denominators of the fractions being added or subtracted. For example, to solve 4/5 – 2/3 = ? the common denominator of 3 and 5 could be 15, 30, 45, etc. For simplicity, the least common multiple, 15, is commonly used. Partitioning fifths into three equal parts creates fifteenths, so 4/5 can be rewritten as 12/15. Partitioning thirds into five equal parts creates fifteenths, so 2/3 can be rewritten as 10/15. Note that renaming a fraction in equivalent form is like multiplying by one, in fraction form. 4/5 x 3/3 = 12/15 and 2/3 x 5/5 = 10/15. 3/3 and 5/5 are names for one.
Once 4/5 and 2/3 are renamed as equivalent fractions with the same denominator the units are of equal size and can be separated or compared. So, 4/5 – 2/3 can be rewritten as 12/15 – 10/15 = 2/15. Therefore the problem becomes 12/15 – 10/15 and gives the answer 2/15.
The learning opportunities in this unit can be differentiated by providing or removing support to students, by varying the task requirements. Ways to support students include:
Tasks can be varied in many ways including:
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. Fractions arise from equal sharing and measuring. Fair shares are a common feature of many cultures, particularly Pasifika communities where effort and reward are communally owned. Sharing food is a cultural universal. With your class, you might come up with a list of contexts in which your students share food (e.g. marae visits, birthday parties, picnics, Christmas). Use these contexts to enhance how the maths learning in the following sessions reflects the cultural diversity of your students. For example, in Polynesian cultures, shares given to families from collective food and materials gathering or hunting, are often based on the number of family members, so the fractions are often unequal.
Measurement contexts are ubiquitous in modern life, due to the use of metric measures. Length, area, mass, volume and capacity occur in everyday settings from allocating water, to creating items from fabric, to calculating loads. Historical measures, such as arm spans, head circumferences, and foot lengths, also provide contexts for use of fractions, arising from the need for accuracy.
Te reo Māori vocabulary terms such as haurua (half), hautoru (third), hauwhā (quarter), hautau ōrite (equivalent fraction) and hautau (fraction) could be introduced in this unit and used throughout other mathematical learning. In te reo Māori, the prefix ‘hau’ refers to how many parts a whole has been divided into. Therefore, number terms such as rima (five) can be added to the ‘hau’ prefix to make ‘haurima’ (fifth). The te reo Māori term for a whole number is tauoti. To talk about non-unit fractions (for example, 2/3), we use the same number-words as we would for counting in te reo Māori. Therefore, two-thirds can be called rua hautoru.
Session 1
SLOs:
For example: “one quarter, two quarters, three quarters, one, one and one quarter, one and two quarters, one and three quarters, two, two and one quarter…”
Use a set of fractions strips (Copymaster 1) to build up a number line model as you count.
Why is 4/4 called one?
Why is 6/4 called 1 ½?
Write on the class/group chart in words and symbols:
Four quarters is the same as one: 4/4 = 1,
Eight quarters is the same as two: 8/4 = 2, etc.
Highlight the equals sign. Ask students to discuss the meaning of = (is the same as, the amount on one side is equivalent in value to the amount on the other side).
Record their ideas.
Equals means the same quantity. So, 8/4 and 2 are two ways to record the same number. At this stage, you could draw on students’ understandings of algebraic equations, if they are familiar with equations such as 2a = 4, so a=2. The equals sign can also be linked to familiar measurement contexts (e.g. weighing items on scales to see if they are equal).
Ask students to work in pairs to reach a solution. Provide Copymaster 2: Pizza Pieces for students to use if needed. Share the strategies as a class and summarise those strategies on the class chart. Encourage students to think flexibly. Prompt thinking with questions like the following:
Are any pairs of fractions easy to add? (e.g. 1 1/8 + 7/8). Why?
How many eighths of a pizza, altogether, are left over?
Can you think of any ways to combine the 1/2 of Hawaiian pizza and 1/4 meat lovers pizza? Would this make it easier or more difficult to count?
Students might divide the total of 6 ½ pizzas and convert that amount into 52/8. Alternatively, they might change each fraction into eighths and total the number of eighths.
Make your own fraction number line, starting at zero and finishing at eight, where the right-hand edge is. Tape both strips together to get a good length.
What number will go on the join?
Where will you locate 1? 7? 4 ½, 6 3/4?
Please show all the halves, quarters, and eighths from 0 to 8.
Watch that students locate all numbers, including fractions, on the marks and not in the spaces.
Have students begin at zero and add 1 1/8 (the vegetarian pizza left over) on the number line. They might use a peg to mark the total amount of pizza each time, as each fraction is added.
How can we figure out where a jump of ¾ more will land? This jump can represent us, adding on the leftover meat lovers pizza?
Three quarters (i.e. 6/8) more than 1 1/8 equals 1 7/8. Then, 1 whole pizza can be added to get 2 7/8 pizza. One might be added first then 7/8 and the answer is the same.
Use your number line to add the fractions of leftovers. Check to see that our original answer is correct.
Roam the room to see that students add the fractions correctly, renaming ones, halves, quarter, and eighths as needed, and recognising when another one (whole) is created.
For some students, it may be appropriate to present these questions orally. However, other students may benefit from questions written on mini whiteboards or sticky notes.
Ask your students to solve the problem by imaging the number line. Ask students to share their results with a partner. Model solving the question - making explicit links to fraction materials to show the relationship between halves, quarters, and wholes. Ensure the recorded fractions are visible for students to see.
Repeat with other examples involving halves, quarters, and eighths. Use pizza pieces to confirm the sums if necessary.
Make a new number line starting at zero and finishing at eight. Join the strips like last time.
This time your number line must show halves, thirds, and sixths.
How will you divide each length of one into thirds?
How will you divide thirds into sixths?
Do they locate the whole numbers correctly?
Is the one third unit made by dividing one into three equal lengths?
Are students aware that one half of one third equals one sixth?
You might align the first and second number lines.
Using our number lines, how many names for 1 ½ can we find?
1 2/4, 6/4, 1 4/8, 12/8, 1 3/6, 9/6.
What would happen if we added 3/4 and 5/6? What would the answer be?
Students should recognise that the answer, 19/12, cannot be expressed as an exact number of quarters or sixths. You might use a fraction strips to show that twelfths are needed to express the answer.
Session Two
SLOs:
For example: John says he needs 3 1/4 of the playing field to set up for a game of Kī-o-Rahi. He sections off the playing field. What portion of the playing field remains?
Let students calculate an answer then check their responses with fractions strips (Copymaster 1). The physical action is removal. Taking away 1 1/4 is straight forward. This leaves a remaining 2/4 to be taken away, leaving a total of 1 2/4 or 1 1/2 of the playing field remaining.
Review strategies from Session 1. Just like with addition, units of the same denominator are needed for subtraction of fractions.
For example: Ihaia is carving a new whakairo for the marae. He has a 4 3/4 metres length of wood. He cuts off 2 1/3 metres. What length of wood is left?
Ask students to work in pairs to attempt the problem. Encourage access to their previous number lines and fraction strips.
How might you find the length that remains? (Either add on to 2 1/3 until you reach 4 ¾ or remove 2 1/3 from 4 ¾).
Estimate the length that remains. (2 metres and a fraction of a metre)
What fraction is ¾ with 1/3 taken away? What sized pieces might fit? (Twelfths)
Record the problem using an empty number line to capture the removal of parts.
What is the problem with 3/4 - 1/3? (Different denominators means different sized pieces)
Could we rename both 3/4 and 1/3 using a different denominator? Which denominator?
Students may have already discovered that twelfths fit the gap between 2 and the answer on the number line.
How many twelfths equal 3/4? How many twelfths equal 1/3? (Align fraction strip pieces if needed to check that 3/4 = 9/12 and 1/3 = 4/12)
4 3/4 - 1 1/3 = 4 9/12 – 2 4/12
= 2 5/12 (subtracting ones first then twelfths)
Why did we need a common denominator of twelve to solve this problem? (Addition and subtraction are only possible if the units are the same.)
It is vital that students recognise that equivalent means of equal value, that is, different expressions of the same quantity. ½ and 5/10 are equivalent because they represent the same amount and occupy the same location on the number line between zero and one.
Refer to the class/group chart recording from Session 1:
4/4 = 1, 8/4 = 2, 12/4 = 3, 16/4 = 4, and the highlighted = sign.
Do students agree that equals means “is the same as” or “that the amount on one side is equal in value to the amount on the other side”?
Use lengthwise folding to illustrate how equivalent fractions can be found.
Here is the example of 2/3 = 4/6 = 8/12 = …
What comes next in the equation? How do you know? (= 16/24 = 32/48 …)
What patterns do you notice in the numbers?
Students should notice that both the numerator and denominator are doubling.
Why did that happen? (With each half fold the number of pieces that make one (denominator) doubled so the number of shaded pieces doubled)
Start with 3/4 and repeatedly halve to get 3/4 = 6/8 = 12/16
Start with 1/2 and repeatedly third to get 1/2 = 3/6 = 9/18
Find as many equivalent fractions as you can using these materials. Record the fractions using equations and diagrams. Create a poster of your work explaining how equivalent fractions work.
Give students plenty of time to explore. Roam the room looking for:
Are students confident with the meaning of numerator as a count, and denominator as the size of pieces counted?
Do students anticipate the relationships among different sized pieces?
Do students anticipate the effect of halving and thirding pieces of a parent fraction?
Do students record equivalence appropriately using equations?
For example:
Session Three
SLOs:
Here are some equivalent fractions that I found:
2/3 = 4/6 = 8/12
I want to mark each fraction on a number line.
How will I find the place to mark two thirds? (Two copies of one third from zero)
How will I find the place to mark four sixths? (Four copies of one sixth from zero)
How will I find the place to mark eight twelfths? (Eight copies of one twelfth from zero)
What other fractions will be equivalent to two thirds?
Look for vertical alignment to check for correct placement of fractions and equivalence.
Provide each student with three blank A4 pieces of paper and ask them to fold the pieces in these ways.
You will need to think about how the paper was folded.
Remember to label each piece with the correct fraction.
Use your paper pieces to show a partner that:
How many sixths are equivalent to three quarters? (3/4 = 9/12 and 1/6 = 2/12. There are 4 ½ sixths in three quarters)
How many eighths are equivalent to one third? (1/3 = 8/24 and 1/8 = 3/24. There are 2 2/3 eighths in one third)
Equivalent fractions:
Ask the students what they notice happening to the numerator (it is doubling each time) and what is happening to the denominator (it is doubling each time).
Ask students how this could be shown. Accept their suggestions, reaching an understanding that it could be shown in this way.
Purpose: to recognise the multiplicative relationship between equivalent fractions)
This game is for two or three players and the rules are included with the Copymaster.
Session Four
SLOs:
Refer to this expression and have the students suggest how the pattern of equivalent fractions continues.
How long can this pattern of making fractions that are equivalent to one half continue?
How do you know? (note that some fractions equal 1/2 but do not arise in the doubled list)
50/100 64/128 36/72 256/512 22/44
The common property of all fractions equivalent to 1/2 is that the denominator is twice the numerator.
Is there a simpler way to write this fraction?
Let students investigate the question in pairs and record their ideas.
Ideas might be:
If we look at the numerators and denominators of the fractions can we know the simplest fraction without using strips?
Record the equality as:
9/12 = 3/4
We know that we can change three quarters into nine twelfths through multiplying by one. We use 3/3 as a name for one.
What would undo multiplying both the numerator and denominator by three?
Students might recognise that 9 ÷ 3 = 3 and 12 ÷ 3 = 4 which gives the numerator and denominator of 3/4.
Provide some other examples of simplifying fractions by identifying a common factor. Use fraction strips to model each problem if needed. Note that students will need to consider twentieths as half of tenths, and twenty fourths as halves of twelfths.
More knowledgeable students may benefit from being extended through the use of word questions. The questions you pose to your students can be enhanced through connections with students’ cultural backgrounds. For example if your learning has involved looking at images of carvings from the local marae, the questions could be posed as “the whakairo (carving) at our local marae is being restored. The artists use grids to divide up the work, but they cannot agree on how much they should work on each. Hone says it is simplest to divide the carving into twelfths, and that he will complete 8/12 of the work. Can you think of a simpler way to write the fraction that Hone has come up with?
In a school context, problems could also be posed around the use of the school playing field (e.g. for Friday afternoon sport).
For example:
8/12 (2/3) 6/10 (3/5) 15/20 (3/4) 9/24 (3/8)
Purpose: To simplify fractions and to identify which fractions can be simplified.
Student pairs share a deck of shuffled playing cards with picture cards and the jokers removed. They each need a pencil and a sheet of paper.
Players take turns to turn over two cards. The first card is the numerator and the second is the denominator. The player records their fraction. Beside the fraction they write a simpler equivalent fraction if they can, showing what they divided both numerator and denominator by. If their partner agrees they tick their recording.
Fractions for which they can find no simpler fraction are recorded and nothing further is added.
For example:
If a player draws a 6 and then an 8, they write 6/8 = ¾, justifies the division factor, and once their partner agrees they can add a tick ✔.
If a player draws a 7 and then a 9, they write 7/9 but no tick is given.
If the fraction is an improper fraction that is changed to a mixed numeral without simplification, no tick is given as this is not simplifying the fraction. For example: 7/2 = 3 ½ earn no tick bit 9/3 = 3/1 does earn a tick.
Students play and record 10 rounds (at least). They should then look closely at the fractions they were able to simplify (✔) and the ones they were not.
They must discuss, agree, and write the ‘Secret to simplifying fractions is…’
For example:
Session Five
SLOs:
When would it be useful to know about equivalent fractions?
Record the students' suggestions and ask them to provide examples. They may offer problems like these:
How much time, in total, has Aria spent creating her kete?
(3/4 + 2/3 = 9/12 + 8/12 = 17/12 = 1 5/12)
How much fabric does Tina have left?
(1 4/5 - 3/4 = 9/5 - 3/4 = 1 16/20 – 15/20 = 1 1/20)
Why is finding a common denominator necessary to solve both problems?
Which common denominators did you use? Why did you choose those numbers?
When did you use equivalent fractions to solve the problems?
What is the best way to find a common denominator?
Let’s use 2/3 + 4/5 as an example.
From previous work students might know that thirds and fifths can be equally partitioned into fifteenths.
How many equal parts is each third broken into, so that fifteenths are formed? (five)
You may need to demonstrate the partitioning with fraction strips. Students need to see that the size of the parts comes from considering how many of those parts make one (whole).
How many fifteenths are equivalent to two thirds? (write 2/3 = 10/15)
We look for the least common multiple of 3 and 5 (LCM) so both fractions can be named with the same denominator.
Shade the multiples of three in one colour; 3, 6, 9, …
Shade the multiples of five in another colour; 5, 10, 15,…
Continue until all the multiples have been found.
How do we know which numbers are common multiples of 3 and 5? (double colour)
What is the least common multiple of 3 and 5? (15)
Let students work on these tasks using Copymaster 4 as support.
Why are the common multiples of 2 and 5 in the right-hand column?
Why is 12 the LCM of 4 and 6, when 4 x 6 = 24?
Why do 7 and 13 have only one common multiple less than 100?
Note that any common multiple will work but LCM is the simplest to use.
Record the thinking using a table like this:
3/4 + 2/3 =
1 4/5 - 3/4
Do your students look for pattern in the occurrence of multiples?
For example, the common multiples of 3 and 8 occur in every eighth cell in the 3 column and row, and every third cell in the 8 column and row.
Can they identify the LCM in each problem?
Purpose: To apply knowledge of equivalent fractions to solving problems.
This is a game for two players. Story cards and fraction cards are shuffled and placed face down in two piles. Each player takes two story cards and 6 fraction cards and places them face up in front of them.
Players take turns to:
The winner is the player that makes the most pairs.
Note: There will be 7 fraction cards left over because some are ‘trick’ cards.
Extra work:
Students could work on some of the Fractions e-ako to consolidate learning of concepts developed in these lessons. These e-ako are at the right hand end of the level 3 shelf on the Additive thinking and Multiplicative thinking pathways.
Students work independently to complete MM8-9 - part 2, explanation of which fraction is larger. Ask them to pair, share, and discuss.
Students watch the following videos to see how a unifix cubes model can be used to add and subtract fractions:
Dear parents and whānau,
In mathematics we have been exploring equivalent fractions. We have learned to play a game called Fraction Fish in which we find equivalent fractions. Your child has brought home a plastic bag containing the playing cards and instructions. They will explain how this is played.
Enjoy the challenge.
Equivalent fractions with sets
This unit introduces students to equivalent fractions. Unlike whole numbers that occupy a unique position on the number line, there is an infinite set of fractions that represent the same value. Fraction that are of equal value are said to be equivalent.
Fractions are an extension of the number system beyond whole numbers so that division answers are possible. For example, equally sharing 3 objects among 2 people is only possible if halves are created. In this unit students deal with the complexity of a whole (one unit) that is composed of a given number of parts. The ‘sets’ model of fractions presents conceptual challenges for students as they need to create units and think with those units (described as re-unitising by Lamon, 2007). Fractions of a set inevitably contain different ones, the individual objects a part is made from, and the one that is the whole.
For example, consider a unit of one (the whole) that is made from 12 cubes. One third of the whole is composed of 4 cubes, since 3 lengths of 4 cubes make the whole.
The whole (one) is made of individual cubes but so are the thirds. To see the parts as thirds a student needs to conceptualise them as such, in relation to one. Defining one as invariant (unchanging) is needed in the creation of a number line to show the relative size of fractions. If the length of 12 cubes is called one, then the place of the thirds fractions is found relative to that whole.
The sets model becomes more complicated when the whole is varied. For example, consider these two sets of 12 objects and 20 objects. Both sets have three quarters of the objects shaded.
Three quarters represents the relationship between the shaded part and the whole of each set. Realising that the relationship is the same though the number of objects is different presents a significant conceptual obstacle yet is essential to students’ understanding of ratio. Notice also that equivalence of fractions takes on new meaning in a sets model. 9 twelfths of the left-hand set and 15 twentieths of the right-hand set are shaded. Writing 9/12 = 15/20 is a way to say that the relationship of shaded part to whole is the same for both fractions. Both fractions are equivalent to 3 quarters requires reunitising individual circles as quarters of the whole.
The learning opportunities in this unit can be differentiated by providing or removing support to students, by varying the task requirements. Ways to support students include:
Tasks can be varied in many ways including:
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. The unit uses contexts like fuel gauges on cars, water tanks, mountain biking and kaimoana, that will resonate with most students. Other contexts involving fractions of lengths might also be engaging for your students. For example, the fraction of a race or journey that has been covered at different points is practically useful. Consuming foods that are linear, such as submarine sandwiches, bananas, or sausages, might motivate some learners. Board games, that have a particular number of steps from start to finish, provide opportunities to look at a fraction of a length made of sub-units. Ratios are found in many contexts, such as “What fraction of our class are female?” and “What fraction of the bikes are mountain bikes” and “What fraction of the cows are Jerseys?”
Prior Experience
It is helpful if students have experience with finding fractions of a fixed whole before attempting this unit. Knowing that the numerator is a counter of number of parts and the denominators tells how many of those parts make one, is important to making sense of ideas in this unit.
Units that develop prior experience with fractions are:
Session One
In this lesson students explore names for fractions of length that is divided into a given number of parts.
Have you ever been in a car that runs out of fuel?
What did the driver do?
How are cars designed so this should not happen?
What fraction of the fuel tank is left?
Discuss how the fraction can be found.
How many parts is the gauge divided into? (12)
Are the marks in the middle of the parts or at the end of them? (At the end)
What number does E represent? (Zero)
What number does F represent? (One – the whole tank)
What fraction is the arrow pointing to? (About 9/12 or 3/4).
What is always true about the size of the parts that the whole tank is broken into? (equal)
What do you think the denominator, bottom number of the fraction, means? (The size of the parts, the number of those parts that make one)
What do you notice about the three fractions? Is there a pattern? (The unit fraction gets smaller as the number of parts increases)
What does 100% mean?
What does 0% mean?
Explain that percentage is like dividing the bar into 100 equal parts, rather than 12, as you did in the fuel tank example.
What does 75% mean? (Some students might estimate or know that 75% is equivalent to 3/4 since 25% equals 1/4)
Can students interpret the denominator of a fraction as the number of equal parts?
Do students recognise the numerator as a count of parts the size of the denominator?
Are students able to create correct parts for a given fraction and battery display? For example, 2/5 of ten as 1/5 of ten = 2 bars, therefore 2/5 of ten = 4 bars.
Do students locate the fractions correctly on the number line?
Do they recognise equivalent fractions occupy the same position?
Session Two
In this lesson students come to see that equivalent fractions occupy the same location on the number line. They notice patterns connecting the numerators and denominators of equivalent fractions.
Why is there a tank on the back of this cottage?
Where is the water collected from?
Rural students or those living on lifestyle blocks will know the importance of collecting and conserving water. Collecting water in tanks may also become more prevalent in New Zealand as water becomes scarce and charges increase.
Is the female farmer correct?
Do they have more water than the young farmer?
Ask your students to discuss the questions in small groups. They must be able to justify their opinion.
Look for students to explain why the two fractions are equivalent, possibly using diagrams to justify their ideas. Use slide 4 to check the relative size of the fractions.
Focus attention on how the ones (tanks) are of equal size and quarters are found by halving then halving. Twelfths are found by making thirds then partitioning each third into four parts.
How much of a full tank is one half greater than two fifths? (One tenth)
Do students interpret the numerator and denominator correctly when shading the fractions of a tank?
Do they write correct equations and inequations?
Can they equally partition one tank into the correct number of parts, by length?
Are their partitions sufficiently accurate to compare the two fractions?
Do they show signs of using multiplication to equally partition, such as ninths are thirds of thirds?
What fractions are made here? (Halves)
If I cut each half in half, what fractions will I have? (Quarters)
If I cut quarters into thirds, like this, what fractions will I have? (Twelfths)
Watch the tank fill. What fraction of the tank is full? (Eight twelfths)
Do eight twelfths have another fraction name? (Two thirds)
Why? (Four twelfths make one third)
What fractions are made here? (Thirds)
If I cut each third in fifths, what fractions will I have? (Fifteenths)
Watch the tank fill. What fraction of the tank is full? (Nine fifteenths)
Do nine twelfths have another fraction name? (Three fifths)
Why? (Three fifteenths make one fifth)
Session Three
In this session students explore naming fractions, and looking for equivalence, when the lengths are different. The context of mountain bike riding is used.
Which cyclist has covered the biggest fraction of their ride?
Students may raise ideas about the length each cyclist has covered. Some may recognise that the bottom rider has completed most of her hill work while the top one has a big hill to climb.
If we just think about the length of their ride, which rider has covered the biggest fraction of their journey?
What makes that difficult to decide? (The tracks are curvy rather than straight)
Does that help you with the fraction of their journey for each biker?
Let students work out the fraction of distance covered (top 12/20 and bottom 8/15). Discuss which fraction is greater. Both fractions are just over one half.
How many twentieths equal one half? (10/20)
How many fifteenths equal one half? (Half of 15 equals 7½ so 7½/15)
Looking at how much more than one half 12/20 and 8/15 are, will be helpful. Since 2/20 (1/10) is more than ½/15 (1/30) the male has ridden the larger fraction. You might use a calculator to show each fraction as a decimal. (12 ÷ 20 = 0.6 and 8/15 = 0.533)
Do students attend to fractions rather than distances?
Can they name the fractions of each journey?
Do they recognise that both fractions are equivalent?
Could each journey be divided into quarters? How? (top: 3km = 1/4, bottom: 2km = 1/4)
How many quarters of their total journey has each rider gone?
Slide 4 shows the comparison when each journey is stretched to the same length, despite the number of kilometres being different.
Both fifteenths and tenths can be joined to form fifths. 3km on the 15km journey equals 1/5 of that journey. 2km on the 10km journey equals 1/5 of that journey. Therefore, 7 out of 15 is 1/15 more than 2/5 and 4 out of 10 is equivalent to 2/5.
Some students may use a rate to solve the problem. 15km is one and one-half times 10km. The bottom rider has travelled 4km and would be expected to travel 1 ½ x 4 = 6km to have the same fraction of a 15km ride.
Create two strips of paper of different lengths, say 15cm and 20cm.
Imagine that these two strips are the length of two different bike rides. I am going to shade in a fraction of each strip to show where the rider has got to.
Use the ruler deliberately to shade 9cm of the 15cm strip and 12cm of the 20cm strip.
Which rider has travelled the bigger fraction of their journey?
How could we figure that out?
Students might observe that the rider in the lower strip has travelled further but they also have further to go. Other might suggest measuring each strip and the length of the shading. The fractions are 9/15 and 12/20 which are equivalent. Look for students to suggest grouping the 15ths and 20ths into fifths or using a calculator to convert the fractions to decimals (Both 0.6).
Session Four
In this session students apply the concept of equivalent fractions to problems with sets of objects. Cooperative logic problems are used to engage students in small group collaborative work. Each group will need three paper plates and a set of interlocking cubes (preferably) though counters will also suffice.
There will be four clues and we need to get them all correct to solve the puzzle.
Slide 1 gives the number of shellfish on each plate (12 and 20). It is easy to match the clue by putting on objects to represent shellfish.
What fractions would work for that clue?
Let students discuss possibilities, such as one half and one half, one quarter and three quarters.
Are they the only possible fractions? How do you know?
What numbers of mussels and oysters work on each plate?
Students may use trial and error to find 1 + 11= 12 and 5 + 15 = 20 satisfy the clue.
Which plate is correct? How do you know?
Students should recognise that only the plate with 20 shellfish matches one of possibilities for fractions found from slide 2.
Have we got enough information to complete the puzzle?
What fraction of the shellfish on the left plate are oysters (tia)? (One third)
Which clue card did you use first? Why?
Were any of the clues not needed?
Run though all the clues to ensure the solution is correct. Ask students to justify that their solution meets each condition.
Solutions are:
Session Five
In this session students are provided with an opportunity to demonstrate their learning about equivalence with fractions, and how to represent fractions on a number line to judge relative size.
Three fifths (3/5) Six tenths (6/10) Twelve twentieths (12/20)
What fraction am I?
I am equivalent to a fraction that has four as the denominator.
I have five as my numerator.
Let students work on the problem and share their ideas. Look for them to organise the clues, such as recording the first clue as:
to consider the possible fractions. There are two possible answers 5/10 or 5/20. Either answer is acceptable if it can be justified.
Dear parents and caregivers,
This week our class have been learning about equivalent fractions that are fractions that look different but represent the same value. For example, one half has an infinite number of fractions equivalent to it, such as 2/4, 5/10, 4/8, 50/100.
We have learned to put fractions on a number line and to find a fraction of a set.
Thanks for supporting our learning.
Equivalent fractions in simple ratios
The purpose of this activity is to support students in recognising when part-whole fractions in two or more ratios are equivalent. In this context, equivalence means the same relationship of two measures, such as the relationship of blueberry to apple juice in a mixture.
Here are two mixtures of blueberry and apple juice.
Which mixture tastes most strongly of blueberry?
Students should notice that both mixtures are one half blueberry and one half apple. Therefore, both mixtures should have the same taste.
Percentages are one way to compare the mixtures. Both mixtures have 50% blueberry and 50% apple.
How can we write the mixtures as ratios?
What patterns do you see?
Record students' ideas in an organised way.
Ideally students will notice that 3/6 and 4/8 are equivalent fractions to one half. They may generalise that all fractions equal to one half have a denominator that is twice the numerator. You might record the equivalent fractions as equalities: 1/2 = 3/6 = 4/8.
You might introduce relevant te reo Māori kupu such as hautau ōrite (equivalent fraction).
Construct several possible mixtures and record the ratios and part-whole fractions.
For example, 5:5 is 5/10 blueberry and 5/10 apple.
Here are two mixtures of blueberry and apple juice. Which mixture will taste most strongly of blueberry?
Students should notice that both mixtures are one third blueberry and two thirds apple. Therefore, both mixtures should have the same taste.
What patterns do you notice?
Students should recognise the halving of the numerator and denominator across the equals sign. They might also see that the denominator is three times the numerator in 4/12 and 4/12.
Next steps
Are these ratios of "blapple" (blueberry apple) juice the same flavour? 3:4 and 9:12
Explain why.
Equivalent Fractions, Decimals, and Percentages
Find equivalent fractions and order fractions.
Know benchmarks for converting between common fractions, decimals and percentages.
Know benchmarks for converting between fractions, decimals and percentages.
Number Framework Stages 7 and 8
Fractions/Decimals/Percentages (Material Master 4-28)
Show 10% as10/100 on a deci-mat. Discuss why it equals 0.1.
The students do examples from Material Master 4–28.
Discuss the answers in class. In particular discuss why a number like 0.05 means and equals 5%. Extend this to problems like 15% = 15/100 = 0.15. The students continue with examples from Material Master 4–28.