The purpose of this series of lessons is to develop understanding of equivalent fractions and the operations of addition and subtraction with fractions.
- Add and subtract fractions with like denominators.
- Explore and record equivalent fractions for simple fractions in everyday use.
- Recognise that equivalent fractions occupy the same place on the number line.
- Recognise and apply the multiplicative relationship between simple equivalent fractions.
- Understand that fractions can have an infinite number of names.
- Apply knowledge of the inverse nature of multiplication and division to simplify fractions.
- Apply knowledge of equivalent fractions to solving problems which involve comparing, adding and subtracting fractions with different denominators.
In this unit students learn to find equivalent fractions and apply equivalence when adding and subtracting fractions with different denominators. A fundamental idea about addition and subtraction is that the units that are combined, separated, or compared are of the same size. In a simple addition problem such as 6 + 7 = 13 it is assumed that 6, 7, and 13 refer to the same units, such as apples, or centimetres.
Addition and subtraction of fractions involves greater complexity than with whole numbers.
For example, 3/4 + 2/5 = ? involves two fractions composed of different units. Three quarters refer to three units that are one quarter in size, while two fifths refer to two units that are one fifth in size. Since quarters and fifths are different sized units they cannot be added. Key to this, is understanding that the denominator in a fraction describes the size of units the fraction is made up of.
Renaming the fractions in units of the same size involves creating a common or "like" denominator. A common denominator can be any common multiple of the denominators of the fractions being added or subtracted. For example, to solve 4/5 – 2/3 = ? the common denominator of 3 and 5 could be 15, 30, 45, etc. For simplicity, the least common multiple, 15, is commonly used. Partitioning fifths into three equal parts creates fifteenths, so 4/5 can be rewritten as 12/15. Partitioning thirds into five equal parts creates fifteenths, so 2/3 can be rewritten as 10/15. Note that renaming a fraction in equivalent form is like multiplying by one, in fraction form. 4/5 x 3/3 = 12/15 and 2/3 x 5/5 = 10/15. 3/3 and 5/5 are names for one.
Once 4/5 and 2/3 are renamed as equivalent fractions with the same denominator the units are of equal size and can be separated or compared. So, 4/5 – 2/3 can be rewritten as 12/15 – 10/15 = 2/15. Therefore the problem becomes 12/15 – 10/15 and gives the answer 2/15.
The learning opportunities in this unit can be differentiated by providing or removing support to students, by varying the task requirements. Ways to support students include:
- continuing work on multiplication and division basic facts through diagnosis and practice of missing facts. Within this, consider what basic facts knowledge your students can easily apply when working with fractions.
- using concrete materials, such as paper strips or sheets, number lines, magnetic fraction tiles, fraction strips or circles, consistently, and with an emphasis on students anticipating the results of actions
- explicitly modelling actions on the materials with appropriate questioning about the fractions involved and the size of one
- linking words and materials to symbols, so that students connect fraction symbols to quantity
- using of a variety of situations to which addition and subtraction are applied. The situations include joining, separating, and comparing quantities
- using more complex fractions and longer, multi-step word problems to extend very capable students.
Tasks can be varied in many ways including:
- beginning with fractions that occur through symmetric partitioning of one, i.e. halves, quarters, eighths, etc., before using more difficult partitions such as thirds, fifths, and sevenths
- working at first with addition and subtraction problems where the equal partitioning of units is easy to enact and visualise, e.g. halves, thirds, quarters
- using physical and diagrammatic models before the use of symbols, then using both together
- grouping students purposefully to encourage supportive tuakana-teina relationships, and collaborative learning.
- prompting explanation and justification from groups of students
- reducing the demands for a product, e.g. diagrams with less reliance on writing equations at first but progressing to fluency with equations
- using digital technology, such as virtual manipulatives, to facilitate visualisation and risk taking.
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. Fractions arise from equal sharing and measuring. Fair shares are a common feature of many cultures, particularly Pasifika communities where effort and reward are communally owned. Sharing food is a cultural universal. With your class, you might come up with a list of contexts in which your students share food (e.g. marae visits, birthday parties, picnics, Christmas). Use these contexts to enhance how the maths learning in the following sessions reflects the cultural diversity of your students. For example, in Polynesian cultures, shares given to families from collective food and materials gathering or hunting, are often based on the number of family members, so the fractions are often unequal.
Measurement contexts are ubiquitous in modern life, due to the use of metric measures. Length, area, mass, volume and capacity occur in everyday settings from allocating water, to creating items from fabric, to calculating loads. Historical measures, such as arm spans, head circumferences, and foot lengths, also provide contexts for use of fractions, arising from the need for accuracy.
Te reo Māori vocabulary terms such as haurua (half), hautoru (third), hauwhā (quarter), hautau ōrite (equivalent fraction) and hautau (fraction) could be introduced in this unit and used throughout other mathematical learning. In te reo Māori, the prefix ‘hau’ refers to how many parts a whole has been divided into. Therefore, number terms such as rima (five) can be added to the ‘hau’ prefix to make ‘haurima’ (fifth). The te reo Māori term for a whole number is tauoti. To talk about non-unit fractions (for example, 2/3), we use the same number-words as we would for counting in te reo Māori. Therefore, two-thirds can be called rua hautoru.
- Unifix cubes
- Adhesive tape
- Packs of playing cards
- Strips of paper made from A3 sized paper
- Hundreds flip board
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- Copymaster 6
Session 1
SLOs:
- Explore and record equivalent fractions for simple fractions in everyday use.
- Recognise that equivalent fraction occupy the same place on the number line.
- Add and subtract fractions with like denominators.
- Begin this session by consolidating students' understandings of where fractions fit on a number line, by skip counting forwards and backwards in common fractions (e.g. 1/2), improper fractions (e.g. 8/2) and mixed fractions (e.g.1 1/2).
For example: “one quarter, two quarters, three quarters, one, one and one quarter, one and two quarters, one and three quarters, two, two and one quarter…”
Use a set of fractions strips (Copymaster 1) to build up a number line model as you count.
Why is 4/4 called one?
Why is 6/4 called 1 ½?
- Ask “How do we write 1 using quarters?” (4/4). How do we write 2 (8/4), 3 (12/4) and 4 (16/4)?
Write on the class/group chart in words and symbols:
Four quarters is the same as one: 4/4 = 1,
Eight quarters is the same as two: 8/4 = 2, etc.
Highlight the equals sign. Ask students to discuss the meaning of = (is the same as, the amount on one side is equivalent in value to the amount on the other side).
Record their ideas.
Equals means the same quantity. So, 8/4 and 2 are two ways to record the same number. At this stage, you could draw on students’ understandings of algebraic equations, if they are familiar with equations such as 2a = 4, so a=2. The equals sign can also be linked to familiar measurement contexts (e.g. weighing items on scales to see if they are equal).
- Pose and write this problem on the class/group chart. “There is a pizza party at Elijah’s house. These bits of the pizzas are left over: 1 1/8 vegetarian, 3/4 meat lovers, 1 5/8 pepperoni, 1/2 Hawaiian, 1 1/4 margarita, and 7/8 seafood. Altogether, how much pizza is left over?”
Ask students to work in pairs to reach a solution. Provide Copymaster 2: Pizza Pieces for students to use if needed. Share the strategies as a class and summarise those strategies on the class chart. Encourage students to think flexibly. Prompt thinking with questions like the following:
Are any pairs of fractions easy to add? (e.g. 1 1/8 + 7/8). Why?
How many eighths of a pizza, altogether, are left over?
Can you think of any ways to combine the 1/2 of Hawaiian pizza and 1/4 meat lovers pizza? Would this make it easier or more difficult to count?
Students might divide the total of 6 ½ pizzas and convert that amount into 52/8. Alternatively, they might change each fraction into eighths and total the number of eighths.
- Provide each student pair with sticky tape and two strips of paper of A3 length (42cm).
Make your own fraction number line, starting at zero and finishing at eight, where the right-hand edge is. Tape both strips together to get a good length.
What number will go on the join?
Where will you locate 1? 7? 4 ½, 6 3/4?
Please show all the halves, quarters, and eighths from 0 to 8.
Watch that students locate all numbers, including fractions, on the marks and not in the spaces.
- Once students complete their number lines, refer to the fractions in the pizza problem posed in part 3 above.
Have students begin at zero and add 1 1/8 (the vegetarian pizza left over) on the number line. They might use a peg to mark the total amount of pizza each time, as each fraction is added.
How can we figure out where a jump of ¾ more will land? This jump can represent us, adding on the leftover meat lovers pizza?
Three quarters (i.e. 6/8) more than 1 1/8 equals 1 7/8. Then, 1 whole pizza can be added to get 2 7/8 pizza. One might be added first then 7/8 and the answer is the same.
Use your number line to add the fractions of leftovers. Check to see that our original answer is correct.
Roam the room to see that students add the fractions correctly, renaming ones, halves, quarter, and eighths as needed, and recognising when another one (whole) is created.
- Pose other problems; e.g. 2 1/2 + 3/4 + 3/4 + 1 3/4 + 3/4 = ☐
For some students, it may be appropriate to present these questions orally. However, other students may benefit from questions written on mini whiteboards or sticky notes.
Ask your students to solve the problem by imaging the number line. Ask students to share their results with a partner. Model solving the question - making explicit links to fraction materials to show the relationship between halves, quarters, and wholes. Ensure the recorded fractions are visible for students to see.
Repeat with other examples involving halves, quarters, and eighths. Use pizza pieces to confirm the sums if necessary.
- Provide each group with two more strips and a piece of sticky tape. Pose the following challenge:
Make a new number line starting at zero and finishing at eight. Join the strips like last time.
This time your number line must show halves, thirds, and sixths.
How will you divide each length of one into thirds?
How will you divide thirds into sixths?
- Roam the room as students work.
Do they locate the whole numbers correctly?
Is the one third unit made by dividing one into three equal lengths?
Are students aware that one half of one third equals one sixth?
- Gather the class and discuss and chart key learning from this session. Focus students’ attention on the need for a common denominator when joining fractions (addition) and that the same quantity may be represented with different fractions.
You might align the first and second number lines.
Using our number lines, how many names for 1 ½ can we find?
1 2/4, 6/4, 1 4/8, 12/8, 1 3/6, 9/6.
What would happen if we added 3/4 and 5/6? What would the answer be?
Students should recognise that the answer, 19/12, cannot be expressed as an exact number of quarters or sixths. You might use a fraction strips to show that twelfths are needed to express the answer.
Session Two
SLOs:
- Add and subtract fractions with like denominators
- Explore and record equivalent fractions for simple fractions in everyday use.
- Recognise that equivalent fractions occupy the same place on the number line.
- Recognise and apply the multiplicative relationship between simple equivalent fractions.
- Understand that fractions can have infinite number of names.
- Begin the session by posing a subtraction problem in which the denominators are the same.
For example: John says he needs 3 1/4 of the playing field to set up for a game of Kī-o-Rahi. He sections off the playing field. What portion of the playing field remains?
Let students calculate an answer then check their responses with fractions strips (Copymaster 1). The physical action is removal. Taking away 1 1/4 is straight forward. This leaves a remaining 2/4 to be taken away, leaving a total of 1 2/4 or 1 1/2 of the playing field remaining.
Review strategies from Session 1. Just like with addition, units of the same denominator are needed for subtraction of fractions.
- Pose a problem in which the denominators are not easily related.
For example: Ihaia is carving a new whakairo for the marae. He has a 4 3/4 metres length of wood. He cuts off 2 1/3 metres. What length of wood is left?
Ask students to work in pairs to attempt the problem. Encourage access to their previous number lines and fraction strips.
- Support students using the strip model and scaffolding questions like:
How might you find the length that remains? (Either add on to 2 1/3 until you reach 4 ¾ or remove 2 1/3 from 4 ¾).
Estimate the length that remains. (2 metres and a fraction of a metre)
What fraction is ¾ with 1/3 taken away? What sized pieces might fit? (Twelfths)
- After an appropriate time, gather the class and discuss their strategies. Model the problem with fraction strips so symbols can be related to quantities. Be explicit in your description of subtracting the fractions.
Record the problem using an empty number line to capture the removal of parts.
What is the problem with 3/4 - 1/3? (Different denominators means different sized pieces)
Could we rename both 3/4 and 1/3 using a different denominator? Which denominator?
Students may have already discovered that twelfths fit the gap between 2 and the answer on the number line.
How many twelfths equal 3/4? How many twelfths equal 1/3? (Align fraction strip pieces if needed to check that 3/4 = 9/12 and 1/3 = 4/12)
- Use equations to model the problem:
4 3/4 - 1 1/3 = 4 9/12 – 2 4/12
= 2 5/12 (subtracting ones first then twelfths)
Why did we need a common denominator of twelve to solve this problem? (Addition and subtraction are only possible if the units are the same.)
- Write on the class/group chart: “What is meant by an equivalent fraction?”
It is vital that students recognise that equivalent means of equal value, that is, different expressions of the same quantity. ½ and 5/10 are equivalent because they represent the same amount and occupy the same location on the number line between zero and one.
- Record student responses, including examples they give, e.g. 1/2 = 2/4
Refer to the class/group chart recording from Session 1:
4/4 = 1, 8/4 = 2, 12/4 = 3, 16/4 = 4, and the highlighted = sign.
Do students agree that equals means “is the same as” or “that the amount on one side is equal in value to the amount on the other side”?
- Provide students with paper strips of the same length cut from photocopy paper.
Use lengthwise folding to illustrate how equivalent fractions can be found.
Here is the example of 2/3 = 4/6 = 8/12 = …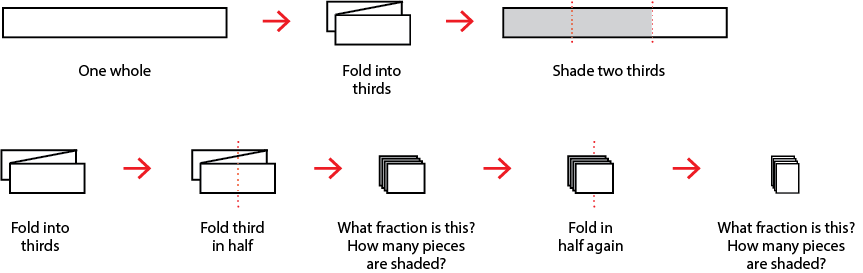
- Record equivalence equations, e.g. 2/3 = 4/6 = 8/12.
What comes next in the equation? How do you know? (= 16/24 = 32/48 …)
What patterns do you notice in the numbers?
Students should notice that both the numerator and denominator are doubling.
Why did that happen? (With each half fold the number of pieces that make one (denominator) doubled so the number of shaded pieces doubled) - Provide two other examples of folding such as:
Start with 3/4 and repeatedly halve to get 3/4 = 6/8 = 12/16
Start with 1/2 and repeatedly third to get 1/2 = 3/6 = 9/18
- Provide your students with Fraction Strips (Copymaster 1) and Pizza Pieces (Copymaster 2).
Find as many equivalent fractions as you can using these materials. Record the fractions using equations and diagrams. Create a poster of your work explaining how equivalent fractions work.
Give students plenty of time to explore. Roam the room looking for:
Are students confident with the meaning of numerator as a count, and denominator as the size of pieces counted?
Do students anticipate the relationships among different sized pieces?
Do students anticipate the effect of halving and thirding pieces of a parent fraction?
Do students record equivalence appropriately using equations? - After a suitable time, gather the class to share their posters. Look for patterns in the equations, particularly the multiplying and dividing of numerators and denominators by the same factor.
For example: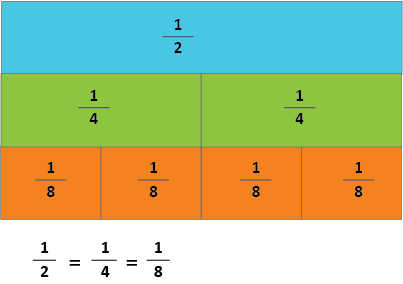
- These fractions are equivalent
- They are the same length
- The fractions have the same value
Session Three
SLOs:
- Recognise that equivalent fractions occupy the same place on the number line.
- Recognise and apply the multiplicative relationship between simple equivalent fractions.
- Have students relook at their equivalent fraction posters. Together record on the class/group chart what the students notice about equivalent fractions highlighting that equivalent fractions:
- have the same value
- have the same length
- have different numerators and denominators.
- Given each pair of students two strips of paper cut longways from A3 paper.
Here are some equivalent fractions that I found:
2/3 = 4/6 = 8/12
I want to mark each fraction on a number line.
- Start by using a one length from the fraction strip set to mark zero and one respectively at the left and right ends.
How will I find the place to mark two thirds? (Two copies of one third from zero)
How will I find the place to mark four sixths? (Four copies of one sixth from zero)
How will I find the place to mark eight twelfths? (Eight copies of one twelfth from zero)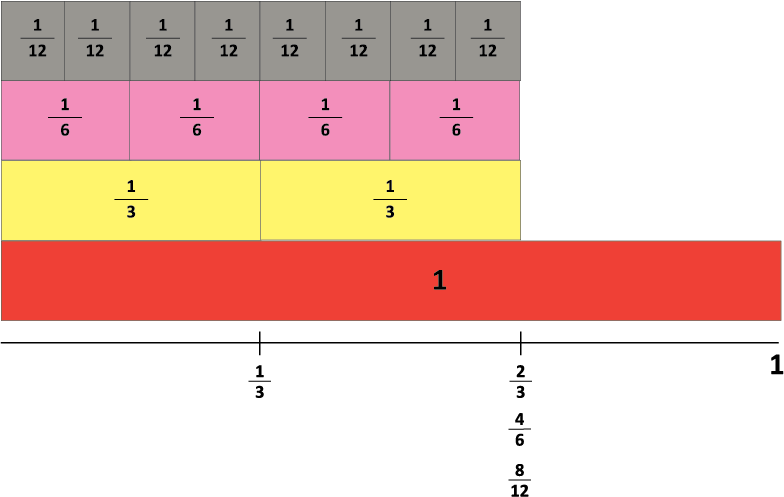
What other fractions will be equivalent to two thirds?
- Ask your students to create a number line showing some of the equivalent fractions that they identified. After a suitable time gather the strips and arrange them vertically on a wall or board.
Look for vertical alignment to check for correct placement of fractions and equivalence.
- We have used lengths. I wonder if equivalence also works with areas.
Provide each student with three blank A4 pieces of paper and ask them to fold the pieces in these ways.
You will need to think about how the paper was folded.
Remember to label each piece with the correct fraction.
- Gather the class.
Use your paper pieces to show a partner that:- Three quarters are equivalent to six eighths (3/4 = 6/8).
- Two thirds are equivalent to eight twelfths (2/3 = 8/12).
- Five sixths are equivalent to twenty twenty-fourths (5/6 = 20/24).
- Allow students sufficient time to rehearse their demonstrations of equivalence. Look for signs of students noticing relationships among unit fractions, such as twenty-fourths are quarters of sixths.
- Share the results as a class, sticking the appropriate paper pieces on a board to check equivalence of area. You might try less obvious examples where the multiplying numerator and denominator by a whole number factor does not work. Good counter examples are:
How many sixths are equivalent to three quarters? (3/4 = 9/12 and 1/6 = 2/12. There are 4 ½ sixths in three quarters)
How many eighths are equivalent to one third? (1/3 = 8/24 and 1/8 = 3/24. There are 2 2/3 eighths in one third)
- Add to the points from the start of the activity:
Equivalent fractions:- have the same value
- have the same length or area
- have different numerators and denominators
- occupy the same place on a number line.
- Write on the class/group chart: 1/2 = 2/4 = 4/8
Ask the students what they notice happening to the numerator (it is doubling each time) and what is happening to the denominator (it is doubling each time).
Ask students how this could be shown. Accept their suggestions, reaching an understanding that it could be shown in this way.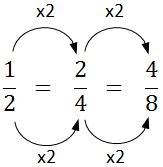
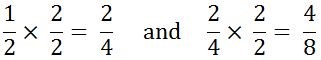
- Together recognise that the value of 2/2 equals 1 and that when any whole number is multiplied by 1 the product equals that number. We can multiply a fraction by 2/2, 3/3, 4/4 etc. to find equivalent fractions without changing the value of the amount represented.
- Ask the students to play Fractions Fish. This game can be made from Copymaster 3.
Purpose: to recognise the multiplicative relationship between equivalent fractions)
This game is for two or three players and the rules are included with the Copymaster.
Session Four
SLOs:
- Understand that fractions can have an infinite number of names.
- Understand the inverse nature of multiplication and division and how this knowledge can be used to simplify fractions.
- Use multiplication and division to calculate equivalent fractions.
- Begin this session by reading together the final statement made in Session 3.
Refer to this expression and have the students suggest how the pattern of equivalent fractions continues.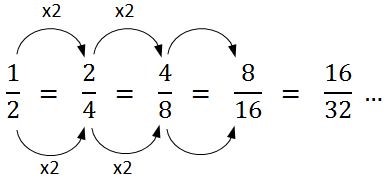
How long can this pattern of making fractions that are equivalent to one half continue?
- Have students discuss this in pairs and agree on their answer. “Forever. We can just keep on going”.
- Ask: Which of these fractions would be in the list equivalent to one half?
How do you know? (note that some fractions equal 1/2 but do not arise in the doubled list)
50/100 64/128 36/72 256/512 22/44
The common property of all fractions equivalent to 1/2 is that the denominator is twice the numerator.
- Discuss and conclude that there are an infinite number of names for any fraction. You might try other fractions such as 2/3 and 3/5 to see if you run out of possible equivalent fractions. For example: 2/3 x 3/3 = 6/9 = 18/27 = 54/81 = …
- Write 9/12.
Is there a simpler way to write this fraction?
Let students investigate the question in pairs and record their ideas.
Ideas might be:- We went ‘backwards’ (divided the numerator and denominator by 2 several times).
- We know that 3/12 is the same as ¼.
- We know that 9 is three quarters of 12.
- Create a fraction strip picture of the problem:
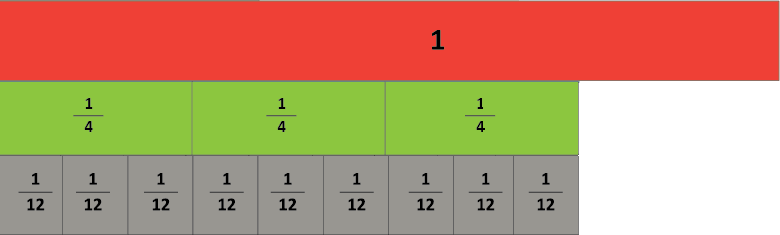
If we look at the numerators and denominators of the fractions can we know the simplest fraction without using strips?
Record the equality as:
9/12 = 3/4
We know that we can change three quarters into nine twelfths through multiplying by one. We use 3/3 as a name for one.
What would undo multiplying both the numerator and denominator by three?
Students might recognise that 9 ÷ 3 = 3 and 12 ÷ 3 = 4 which gives the numerator and denominator of 3/4.
Provide some other examples of simplifying fractions by identifying a common factor. Use fraction strips to model each problem if needed. Note that students will need to consider twentieths as half of tenths, and twenty fourths as halves of twelfths.
More knowledgeable students may benefit from being extended through the use of word questions. The questions you pose to your students can be enhanced through connections with students’ cultural backgrounds. For example if your learning has involved looking at images of carvings from the local marae, the questions could be posed as “the whakairo (carving) at our local marae is being restored. The artists use grids to divide up the work, but they cannot agree on how much they should work on each. Hone says it is simplest to divide the carving into twelfths, and that he will complete 8/12 of the work. Can you think of a simpler way to write the fraction that Hone has come up with?
In a school context, problems could also be posed around the use of the school playing field (e.g. for Friday afternoon sport).
For example:
8/12 (2/3) 6/10 (3/5) 15/20 (3/4) 9/24 (3/8)
- Summarise the findings about how to simplify fractions:
- To simplify a fraction, you can divide both the numerator and the denominator by the same whole number.
- Multiplication and division are inverse operations, one undoes the other.
- Ask students to play Simplify Secrets in pairs.
Purpose: To simplify fractions and to identify which fractions can be simplified.
Student pairs share a deck of shuffled playing cards with picture cards and the jokers removed. They each need a pencil and a sheet of paper.
Players take turns to turn over two cards. The first card is the numerator and the second is the denominator. The player records their fraction. Beside the fraction they write a simpler equivalent fraction if they can, showing what they divided both numerator and denominator by. If their partner agrees they tick their recording.
Fractions for which they can find no simpler fraction are recorded and nothing further is added.
For example:
If a player draws a 6 and then an 8, they write 6/8 = ¾, justifies the division factor, and once their partner agrees they can add a tick ✔.
If a player draws a 7 and then a 9, they write 7/9 but no tick is given.
If the fraction is an improper fraction that is changed to a mixed numeral without simplification, no tick is given as this is not simplifying the fraction. For example: 7/2 = 3 ½ earn no tick bit 9/3 = 3/1 does earn a tick.
Students play and record 10 rounds (at least). They should then look closely at the fractions they were able to simplify (✔) and the ones they were not.
They must discuss, agree, and write the ‘Secret to simplifying fractions is…’
- Bring the class together after the game to generalise that a fraction can be simplified if both numerator and denominator share a common factor.
- For practice in finding equivalent fractions, ask students to independently complete MM8-9 part 1, Equivalent fractions: Equation and Explanation.
- On the class/group chart summarize what has been learned in this session.
For example:- A fraction can have an infinite number of names if we keep on multiplying the numerator and denominator by the same number.
- Some fractions can be simplified by evenly dividing the numerator and denominator by the same number.
Session Five
SLOs:
- Recognise and apply the multiplicative relationship between simple equivalent fractions.
- Apply knowledge of equivalent fractions to solving problems which involve comparing, adding and subtracting fractions with different denominators.
- Begin by posing the question:
When would it be useful to know about equivalent fractions?
Record the students' suggestions and ask them to provide examples. They may offer problems like these:- If we are comparing different kinds of fractions to see which fraction is greater. Like you might have 3/4 of metre of fabric and you need 2/3 metre. Will you have enough?
- If we are adding different fractions. Say you had 3/4 of a pizza and another 1/3 of a pizza. Does that make 1 whole pizza?
- If you have an amount and gave away a fraction, and you want to work out what you have left. Like you have 5/8 of something and you gave away 1/4.
- Provide these two problems for students to solve in pairs, before sharing with the class.
- Aria wants to weave a kete. Collecting the harakeke takes 3/4 of an hour learning how to weave from her kuia.
How much time, in total, has Aria spent creating her kete?
(3/4 + 2/3 = 9/12 + 8/12 = 17/12 = 1 5/12) - Tina has 1 4/5 metres of fabric that she can use to make poi. She uses 3/4 of the fabric.
How much fabric does Tina have left?
(1 4/5 - 3/4 = 9/5 - 3/4 = 1 16/20 – 15/20 = 1 1/20)
- Aria wants to weave a kete. Collecting the harakeke takes 3/4 of an hour learning how to weave from her kuia.
- Model each problem with fraction strips. Discuss:
Why is finding a common denominator necessary to solve both problems?
Which common denominators did you use? Why did you choose those numbers?
When did you use equivalent fractions to solve the problems?
- Pose the question:
What is the best way to find a common denominator?
Let’s use 2/3 + 4/5 as an example.
From previous work students might know that thirds and fifths can be equally partitioned into fifteenths.
How many equal parts is each third broken into, so that fifteenths are formed? (five)
You may need to demonstrate the partitioning with fraction strips. Students need to see that the size of the parts comes from considering how many of those parts make one (whole).
How many fifteenths are equivalent to two thirds? (write 2/3 = 10/15)
- Ask the same questions for four fifths (Fifths are cut into three equal parts to form fifteenths so 4/5 = 12/15)
- Summarise:
We look for the least common multiple of 3 and 5 (LCM) so both fractions can be named with the same denominator.
- Provide students with Copymaster 4 which is a sheet of hundreds boards. Show how the common multiples of 3 and 5 can be found. Students can copy you on their page.
Shade the multiples of three in one colour; 3, 6, 9, …
Shade the multiples of five in another colour; 5, 10, 15,…
Continue until all the multiples have been found.
How do we know which numbers are common multiples of 3 and 5? (double colour)
What is the least common multiple of 3 and 5? (15)
Let students work on these tasks using Copymaster 4 as support.- Find the common multiples of 2 and 3?
- Find the common multiples of 2 and 5?
- Find the common multiples of 5 and 6?
- Find the common multiples of 4 and 6?
- Find the common multiples of 7 and 13?
- Discuss the results. Pay attention to:
Why are the common multiples of 2 and 5 in the right-hand column?
Why is 12 the LCM of 4 and 6, when 4 x 6 = 24?
Why do 7 and 13 have only one common multiple less than 100?
- When we solve a problem like 1/3 + ½ = □ what common denominator might we use? Why?
Note that any common multiple will work but LCM is the simplest to use.
Record the thinking using a table like this:
- Use the same format to capture finding the common denominator for the problems in section 2.
3/4 + 2/3 =
1 4/5 - 3/4
- Ask your students to do more work with Common Multiples (Copymaster 5). Some students will need support to understand what is required. If necessary, model solving the first problem then encourage students to work independently.
- Roam the room and look for:
Do your students look for pattern in the occurrence of multiples?
For example, the common multiples of 3 and 8 occur in every eighth cell in the 3 column and row, and every third cell in the 8 column and row.
Can they identify the LCM in each problem?
- Have students play the game, I can make it, in pairs. (Copymaster 6).
Purpose: To apply knowledge of equivalent fractions to solving problems.
This is a game for two players. Story cards and fraction cards are shuffled and placed face down in two piles. Each player takes two story cards and 6 fraction cards and places them face up in front of them.
Players take turns to:- Check if one of their fraction cards allows them to answer one of the problems, one the problem card. If so, the player matches the two cards and puts the two cards together as a pair. Player Two checks the match.
- Whether they can make a pair or not the player adds an extra fraction and problem card from the two piles, or they propose a swap of one of each type of card with the other player.
The winner is the player that makes the most pairs.
Note: There will be 7 fraction cards left over because some are ‘trick’ cards.
- Ask each student to write at least three contextual addition or subtraction of fractions problems for a partner to solve. Each problem must have a model answer. Make a class book of addition and subtraction problems.
Extra work:
Students could work on some of the Fractions e-ako to consolidate learning of concepts developed in these lessons. These e-ako are at the right hand end of the level 3 shelf on the Additive thinking and Multiplicative thinking pathways.
Students work independently to complete MM8-9 - part 2, explanation of which fraction is larger. Ask them to pair, share, and discuss.
Students watch the following videos to see how a unifix cubes model can be used to add and subtract fractions:
- Adding using improper fractions (mp4, 9MB)
- Adding using mixed numerals (mp4, 8.5MB)
Dear parents and whānau,
In mathematics we have been exploring equivalent fractions. We have learned to play a game called Fraction Fish in which we find equivalent fractions. Your child has brought home a plastic bag containing the playing cards and instructions. They will explain how this is played.
Enjoy the challenge.