This unit develops the concept of a fraction as an operator, or multiplier, acting on an amount, e.g. two-thirds of 24. Using fraction multipliers to represent the relationship between different amounts is also explored.
- Find a unit and non-unit fraction of a set, e.g. two thirds of 24 (2/3×24).
- Use a fraction to represent the relationship between part of a set and the whole set.
- Recognise when the fractions of two different sized sets are equivalent, and when one fraction is greater than another.
- Use a fraction to represent the relative size of two sets, e.g. 12 is two thirds of 18.
Fractions are an extension of whole numbers and integers. Fractions are needed when wholes (ones) are not adequate for a task. Division often requires equal partitioning of ones. Sharing two chocolate bars equally among five people requires that the bars be cut into smaller equal parts. The operation might be recorded as 2÷5=2/5. Note that the number two fifths, is composed of two units of one fifth. In practical terms the equal share can occur by dividing each of the two bars into fifths, then giving each person one fifth from each bar.
Many contexts involve relating the relative size of discrete quantities, that is, quantities that are collections of individual items. According to Tadanobu Watanabe there are two types of relationship, part to whole, and whole to whole.
- Part to whole
Fractions can represent the relationship between part of a set and the whole set. In the diagram below one quarter or four eighths of the whole set is grey.
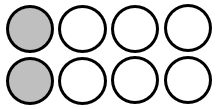
- Whole to whole
Fractions can represent the relationship between two independent sets or amounts. To complicate matters the sets can be within a whole set, as in a ratio situation.
In the left-side diagram, the grey set has three quarters or six eighths of the number of items that the white set has. In the right-side diagram, there are three quarters as many grey circles than there are white circles, within the same set.
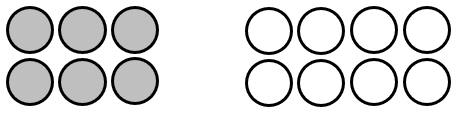
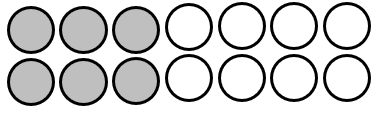
Set to set comparisons are common in the real world, in situations like comparing prices with those some time ago, calculating lambing or calving rates, measuring population growth. Part-whole comparisons are particularly important in situations like comparing groups in statistics, finding the most accurate goal shooter, or sharing sets equally.
Set models tend to be more complex than continuous models like lengths, areas, and volumes, though measurement attributes vary in perceptual difficulty. Set models have the added complexity of competing wholes (ones). Suppose that a box has 12 chocolates, and three of them are strawberry flavour.

To establish that one quarter of the set is strawberry requires imagining the 12 chocolates as one whole set, when each chocolate is a whole in its own right. Establishing quarters requires imagining the three wholes as one quarter, relative to the whole set.
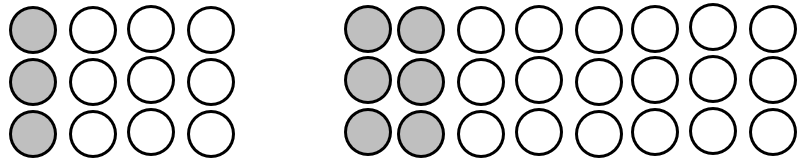
Comparison of fractions, and equivalence of fractions is particularly challenging with sets models. The fraction of grey circles in the left-side set can be expressed as 1/4 or 3/12. The fraction of grey circles in the right-side set can be expressed as 1/4, 2/8, 3/12 or 6/24. Each expression requires you to imagine the set as a whole and create different partitions of that whole. Note that both sets have the same fraction of grey although the size of the sets are different.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- simplifying the fractions involved in problems to those directly related by halving, such as halves, quarters, and eighths, and to those easily accessible through knowledge of basic multiplication facts, like fifths and tenths
- providing scaffolded support to students, particularly through using physical materials, and diagrams, progressing to more abstract symbolic representations
- connecting materials, words, and symbols through meaningful contexts. The meaning of numerator as counter, denominator as size of parts with reference to one, and multiplication as “of” are significant in this unit.
The context for this unit is toppings put of pizza. While most students are familiar with pizza as a common food, other contexts may be more meaningful to your students. Activities can be adapted to suit the interests and experiences of your students. For example:
- A pizza might be exchanged for a plot in a community garden. The plot is shared into equal parts for different numbers of people to farm it. Pizza toppings can be replaced by different seedlings, such as lettuce, spinach, cabbage, and tomato.
- Circular loaves of rēwena (potato bread) might be used instead of pizza. Toppings, such as sesame or pumpkin seeds might be used instead of pizza toppings.
Te reo Māori vocabulary terms such as hautau waetahi (unit fraction), tau whakarea (multiplier) and rautaki whakarea (multiplicative strategy) could be introduced in this unit and used throughout other mathematical learning.
- Unifix cubes, counters
- Blank cubes or dice and stickers (to make dice)
- Scissors
- Calculators (optional)
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- Copymaster 6
- Note that some Copymasters are designed to be copied, laminated and cut up as cards or puzzle pieces.
- PowerPoint 1
- PowerPoint 2
- PowerPoint 3
- PowerPoint 4.
Getting Started
In this lesson students connect circular region models of fractions with finding fractions of a set. By the end of the lesson students should be able to unitise a given set into different parts, and name the part-whole relationships in terms of those parts.
Begin with PowerPoint 1 that presents the scenario of distributing toppings, like pieces of salami, evenly around a pizza. Students are often familiar with a circular region model so the connection to a discrete model is useful.
For each scenario (topping) ask questions like:
- How many (toppings) do you think will go in each piece (unit fraction)?
- How did you work that out?
- How might the equal sharing be written as an equation?
Note that the problems are about finding a unit fraction of a set, so the fraction behaves as a multiplier. Therefore, the equation might be written as multiplication or division, e.g. 1/4×36=9 or 36÷4=9. Students who use additive build up to anticipate the result should be encouraged to use multiplicative thinking with questions like:
- I see you gave four (toppings) to each person, and went 4 + 4 = 8, 8 + 8 =16, to work out how many were used up. What multiplication fact could you use instead?
- Could you give each piece ten (toppings)? Why or why not?
- If ten is too much/little then how could you fix that up?
The final question is about finding a multiplication or division fact that approximates the solution, from which the student can derive the solution. For example, 40 ÷ 5 = 8 can be derived from 10 ÷ 5 = 2 (See Slide Four).
After working through PowerPoint 1, ask students to work on Copymaster 1 in pairs. The problems all involve finding a unit fraction of a set, in the same pizza scenario. You might make materials, like counters, available to some students but encourage them to anticipate the result of the equal sharing first. Look for your students to:
- Apply multiplicative strategies rather than counting or additive build up;
- Record symbols or diagrams to support their thinking;
- Record the situation correctly as a multiplication equation;
- See connection among the problems, that is, use one result to get another.
After completing Copymaster One, students play The Pizza Game. Cards for the game are made from Copymaster 2. Print two sets of the Copymaster to make a total of 32 cards. The game is played with two or three players. Each team of players needs two dice made from blank wooden cubes, or by using stickers over normal dice. The dice are labelled:
Easy Game: 14, 15, 16, 18, 20, 24, and 25, 27, 30, 32, 36, 40.
Hard Game: 35, 36, 40, 42, 45, 48, and 50, 54, 56, 64, 72, 81.
Spread all the cards in the middle, face up so all players can see them.
How to play
Players take turns to:
- Roll the two dice. Choose one of the dice numbers.
- Choose a pizza card so that the number of toppings on the dice can be shared equally onto the pizza with no remainder. The player must explain how they know each piece will have the same number of toppings.
- If the player is correct, they keep that pizza card and it cannot be used again.
- If they are challenged by the other players, and are incorrect, the pizza card stays in the middle.
The winner is the person with the most pizza cards when play finishes, or when all pizza cards are gone.
Exploring
In the following two sessions students extend their knowledge of fractions as multipliers (operators) to non-unit fractions, that is fractions with whole numbers greater than one as the numerator, e.g. 2/3 and 4/5. Then students explore the part-whole relationships in ratios, using fractions to represent relationships.
Session Two
Begin with PowerPoint 2 that shows how to find a non-unit fraction of a set. Progress to Slide 6. Students will notice that the first four slides are the same as PowerPoint 1.
- What is the same about the problems so far?
- How do we solve problems like this?
Students should suggest that the number of toppings is divided by the number of pieces. Why? (To establish the unit fraction). Then the unit fraction is multiplied by the number of pieces that are eaten.
Take at least two of the examples from PowerPoint 2 and write equations for the situations.
- 2/3×30=20 (Two thirds of 30)
- 3/4×32=24 (Three quarters of 32)
- 4/5×35=28 (Four fifths of 35)
Discuss the meaning of the x symbol as ‘of’ and how the numerator and denominator of the operating fraction impact on the calculation, e.g. 4/5 is found by dividing by five then multiplying by four.
Put the students into groups of four and provide the puzzles made from Copymaster 3. There are five puzzles. Each student gets one card for each puzzle. They must work with their team-mates to find a solution that matches all the clues. Each player must ‘own’ their clue, that is, ensure that they retain it and that the solution matches their clue. Encourage the students to record their strategies in some way on paper.
Look for your students to:
- Identify the information that is missing. The information might be numerator or denominator of the operating fraction, the whole number of toppings, or the part of the whole consumed.
- Record the problem symbolically or diagrammatically in ways that are helpful. For example, expressing Puzzle C as 2/3×?=32.
- Use multiplicative strategies to solve the puzzles, rather than resort to drawing and "share by ones" or composite groups (skip counting) strategies. Note that access to a basic facts chart may help some students to think multiplicatively.
After an appropriate time bring the class back together. Focus on one or two puzzles that brought out interesting strategies. Choose groups to share their solutions. An important idea is that either order of multiplying by the numerator and dividing by the denominator works. Usually dividing first is more efficient.
Session Three
Begin with the game “3 in a line.” Gameboards can be printed and laminated using Copymaster 4. The game requires students to practise finding non-unit fractions of whole numbers. An important feature of the game is that equivalent fractions operating on the same whole numbers produce the same product, e.g. 3/4×24=18 and 6/8×24=18.
3 in a line
You need:
- Gameboard for each pair (Version D is harder than the others)
- Two colours of counters and two paperclips
To play:
Players take it in turns to choose a paper clip on their choice of fraction and on their choice of whole number. They find that fraction of the number and, if it is not yet taken, place a counter of their colour on it. The winner is the first player to have three counters of their colour in a row.
Do your students?
- Fluently find non-unit fractions of whole numbers using multiplication and division
- Make strategic choices about which fractions and whole numbers to choose
- Recognise that equivalent fractions operating on the same whole number give the same product
Next return to the pizza context to introduce the concept of part whole fractions within ratios. Use PowerPoint 3 to introduce the concept and provide important questions. Emphasise these key points:
- Fractions can be used to represent the relationships of parts to the whole
- By re-unitising single objects into sets, different fraction names for the same part-whole relationships can be found
- Ratios can be used to represent the relationships among parts that make a whole set.
Let students work on Copymaster 5 individually or in small groups. You might use counters or cubes of various colours to represent the toppings. Manipulation of the ‘toppings’ in physical form can help students as long as they are invited to anticipate the results of division before acting. Look for your students to identify the whole, use fractions to represent the part-whole relationship for each topping, and simply the fraction, if possible, using common factors. The second page of problems requires students to organise a complex set of clues to establish a mix of toppings. Trial and error approaches may be common but encourage your students to organise the clues by usefulness. Physical objects can be useful to try swap ‘toppings’ as clues are considered.
Reflecting
The final session of the unit develops the use of fractions to describe the relationship between different wholes and between parts in the same whole.
Begin with the starting problem on PowerPoint 4. This task is very rich as it involves ideas about area and comparative price, as well as the comparison of toppings.
If you like pepperoni pizza, which are you better to buy, two small pizzas or one large pizza?
Let your students investigate the problem in small groups. Encourage them to develop an argument about which option is best, and their reason for choosing it. After a suitable time gather the class to discuss their answers. Groups should balance at least two characteristics, from area, price, number of pieces of salami, convenience, amount of crust, etc.
Each option is okay because the large pizza is twice the price but is twice as big the little pizza (attending to area though the large pizza is actually 2(1 )/4 times as big).
A response like that contradicts:
The small pizza is better because the larger pizza is only one and one half times as big (attending to diameter) but twice the price as the small pizza.
Note that capable students might calculate the areas (Small: π×132= 530.93cm2; Large: π× 19.52= 1194.59cm2) and provoke a discussion about comparative areas.
Encourage different kinds of comparison, such as:
If you just looked at the number of slices of salami, which option should you go for?
The small pizza has eight pieces of salami while the large pizza has 14 pieces. Buying two small pizzas gives two more pieces of salami for the same price.
Slides 2-9 focus on using fractions to describe the relationships between different numbers of salami pieces (different wholes). The large pizza has 14/8=7/4=1 3/4 as many pieces of salami as the small pizza. Conversely, the small pizza has 8/14=4/7 times as many pieces of salami as the large pizza.
Lining up the collections of pizza pieces makes the comparison easier, but student still need to do the following:
- Establish which collection is the unit to ‘measure’ with
- Compare the other collection to the measurement unit
- Unitise the two collections into common parts
- Express the whole to whole comparison as a fraction operator
Using Copymaster 6 students create a puzzle that involves fractional multipliers. The four pizza cards are put at the corners of a square. Then students place the arrow cards between the pizza cards to represent the correct relationships between the numbers of pieces of salami. For example, the multiplier card ×4/3 goes between the six-piece pizza and the eight-piece pizza, since 6×4/3=8. Let the students solve their puzzle in pairs or threes of mixed ability. Challenge students to consider how the multipliers might be expressed as mixed numbers as well, e.g. ×4/3 can also be expressed as ×1 1/3. Note that most of the operators require simplification using common factors, e.g. ×8/6 is simplified to ×4/3.
As a final challenge students, can use the blank sheets 3 and 4 of Copymaster 6 to create their own puzzle for others to solve.
Kia ora family and whānau,
This week we explored fractions of sets. We used a pizza context to see how to solve problems like “two thirds of 24 equals 16.” The unknown was changed around so sometimes we had to find the product (answer) and other times we had to find the multiplier (fraction) and other time the starting number, like 24. We also explored finding fractions in ratios and identifying the fraction multiplier between amounts.
Pizzas were used as the context for the unit. Ask your child to show you how they can find 3/4 of 20 by putting paper pepperoni slices on a paper circle shaped pizza.