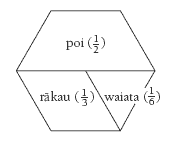This is a level 3 number activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
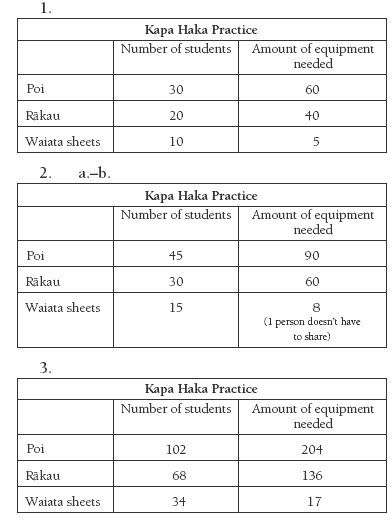
Click on the image to enlarge it. Click again to close. Download PDF (170 KB)
find fractions of a number
Number Framework Links
Use this activity to:
• help the students who are beginning to use early additive strategies (stage 5) to become confident at this stage in all three operational domains (addition and subtraction, multiplication and division, and proportions and ratios)
• encourage transition from early additive strategies (stage 5) to advanced additive strategies (stage 6)
• help your students to consolidate their knowledge of ordering unit fractions and simple equivalences (fractional numbers, stages 5 and 7).
FIO, Levels 2-3, Number Sense and Algebraic Thinking, Book One, Kapa Haka Practice, page 17
A classmate
This activity creates a context in which students work out fractions of a set. They can use a range of strategies in the process, including repeated halving, equal sharing, and using known addition and multiplication facts.
Introduce this activity through a guided teaching group rather than as an independent activity unless your students have strategies at stage 6 or above on the Number Framework. Begin with some mental exercises to practise finding 1/2 and 1/4 of a set, for example, 1/2 of 10, 20, and 30 and 1/4 of 8, 16, and 24.
The students who need to use materials can use the hexagon in a set of international pattern blocks to model the whole group. The trapezium will then represent the 1/2 (the poi), whereas the rhombus will be the using 1/3 rakau. Complete the hexagon with a triangle and ask the students: How much of the whole hexagon is the triangle? When they can see that it represents 1/6 of the whole, make sure that they identify the 1/6 with the rest of the students who will be in the group practising waiata.
When the students understand that 1/6 of the group will practise waiata, check that they understand the connections between the numbers of students and the number of poi, ràkau, and waiata sheets mentioned in the problem.
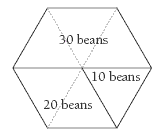
Send the students into small groups to attempt question 1. They should report back before doing question 2. Some students may need to sketch a large hexagon showing the division into 1/2, 1/3, and 1/6. They could use 60 beans or counters to represent the team members and model the solution by sharing out the beans over the hexagon. Encourage the students to use number properties to anticipate the result of equal sharing before they use materials.
The students who use number properties to find 1/3 of the set will either divide by 3 or change the question to 3 x = 60 and ask themselves: “What is the value of the box?”
In question 2, have the students look for an easy way to solve the problem. If necessary, prompt them to use question 1 to help them work out question 2. Note that the number of waiata sheets should be rounded up to the nearest whole number to be sensible.
Question 3 will be more of a challenge. Remind the students that if 204 is too hard to work with, they can split it into easy parts. Send them into groups to find some good splits and report back on these. They may see that 204 = 60 + 60 + 60 + 24, so they only have to work out what share the 24 get because they know what 60 members get from question 1. Similarly, 204 = 180 + 24, so they could use twice the answer for question 2 plus the shares for the extra 24.
Answers to Activity
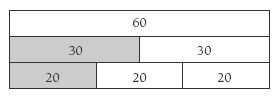
4. Strategies will vary. First you need to find the number of students in each group. You could use a box diagram to help you. This example uses the 60 students from question 1:
Or you could divide 60 by 2 and 3. Once you have the numbers in each group, you can double or divide by 2 to find out how much equipment is needed. For the 90 students, you could use 1 times the 60-student numbers.