In this unit we are exploring ways to find equivalent fractions. We use the concept of equivalent fractions to convert fractions to the benchmark fractions of halves, quarters, thirds, fifths and tenths. From these benchmark fractions it is easier to convert fractions to decimals and percentages. We use equivalent fractions to compare fractions.
- Explore and know equivalent fractions including halves, thirds, quarters, fifths, tenths and hundredths.
- Use equivalent fractions to convert fractions to decimals and percentages.
- Use equivalent fractions to order fractions with different denominators.
Fractions are an extension of whole numbers and integers. Fractions are needed when wholes (ones) are not adequate for a task. Division often requires equal partitioning of ones. Sharing two chocolate bars equally among five people requires that the bars be cut into smaller equal parts. The operation might be recorded as 2 ÷ 5 = 2/5. Note that the number two fifths, is composed of two units of one fifth. In practical terms the equal share can occur by dividing each of the two bars into fifths, then giving each person one fifth from each bar.
If the bar was made up of ten pieces then each person might be given two tenths from each bar, giving them four tenths in total. Four tenths are the same quantity of chocolate as two fifths. Any fraction can be expressed as an infinite number of equivalent fractions that represent the same quantity and occupy the same position on the number line.
Fractions are important to measurement, especially where whole units are not precise enough for the purpose. The symbolic expression does not explain why equivalent fractions represent the same amount. Consider these equivalent fractions: 2/3 = 4/6 = 8/12 . A fraction strip (length) model of the relationships looks like this: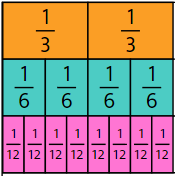
Sixths are half the size of thirds so twice as many sixths fit into the same length as thirds.
Twelfths are quarter the size of thirds so four times as many twelfths fit into the same length as thirds.
The relationship between two thirds and eight twelfths can be represented in this equality.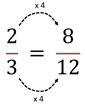
Four times as many twelfths comprise one as thirds. Therefore, each third can be divided into four twelfths.
Understanding equivalent fractions is critical to making sense of decimals and percentages. Consider the names for 3/4 = 0.75 = 75%. Both 0.75 and 75% represent 75/100 which is an equivalent fraction to 3/4. If each quarter is equally partitioned into 25 parts, those parts are called hundredths since 4 x 25 of those parts fit into one.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- varying the level of abstraction
- altering the complexity of the numbers involved, or the relationships between numerators and denominators
- allowing use of scientific calculators that can process fractions
- encouraging sharing and discussion of students’ thinking
- using collaborative grouping so students can support each other and experience both tuakana and teina roles
- encouraging mahi tahi (collaboration) among students.
Adaptation involves changing the contexts used for problems to meet the interests and cultural backgrounds of your students. Where contexts such as food and ratios of orcas and dolphins may not be appropriate for your students, find other situations likely to engage them. Birthday cakes might be replaced by areas of land, dart boards, or gold coins. Orcas and dolphins might be replaced by other animals that need conservation. Linear models are easily applied to journeys that students make, or physical objects such as tape and rope.
Te reo Māori vocabulary terms such as hautau (fraction), hautau ōrite (equivalent fraction), rārangi tau (number line), and haurua, hautoru, hauwhā, haurima… (half, third, quarter, fifth…) could be introduced in this unit and used throughout other mathematical learning.
- Scissors
- Cubes, counters, or other discrete materials of different colours.
- Calculators
- Plastic Fraction Strips (if available) or use Copymaster 4
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- PowerPoint 1
- PowerPoint 2
- PowerPoint 3
Session One
- Begin by writing the fractions 2/3 and 3/4 on the whiteboard.
How do we read these fractions? (two thirds and three quarters)
What picture do you see when you think …about two-thirds? ...about three quarters?
Invite individual students to draw representations of the fractions.
Main points to bring out are:- Two thirds consist of two copies of one third and three quarters is made of three copies of one quarter.
- The numerators (top numbers) are counters of the number of parts, two and three, respectively.
- The denominators give the size of parts, three in 2/3 indicates that the part is one of three equal parts that form one, and four in 3/4 indicates that the part is one of four equal parts that form one.
- Both fractions can be represented as areas (e.g. squares or circles), lengths, sets, and a variety of other ways.
- Use Slide One of PowerPoint 1 to introduce this problem:
Nia and Ashanti are identical twins.
Each birthday they each get identical birthday cakes.
Nia eats two thirds of her cake and Ashanti eats three quarters of her cake.
Who eats the most?
How much more cake does she eat than her sister? - Let students collaborate (mahi tahi) to solve the problem in pairs. Expect them to record how they solved the problem using drawing, symbols, or a combination. As they work, roam the room. Look for students’ understanding that:
- Three quarters is more than two thirds (Why?)
- Twelfths are needed to find the difference between 2/3 and 3/4.
- After a suitable time, gather the class to discuss their solutions. You might use a fraction circle manipulative online, or fold squares or rectangular pieces of paper to find the difference between the two fractions.
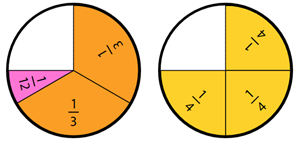
- Discuss why the difference is one twelfth (more obvious with the pre labelled circle pieces). Students might notice that the denominators multiply to give 12 (3 x 4 = 12).
- Ask each student to take two rectangular pieces of paper to represent the birthday cakes. Fold one lengthways into thirds, and shade two thirds. Fold the other rectangle in quarters lengthways and shade three quarters.
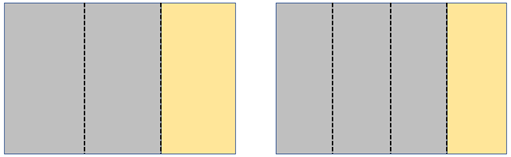
- Fold the pieces of paper back to the unit fractions thirds and quarters.

- Fold the thirds into four equal parts lengthways.
What fraction of the whole cake is each piece? (twelfths – Why?)
How many twelfths are shaded?
Two thirds equals how many twelfths? - Fold the quarters into three equal parts lengthways.
What fraction of the whole cake is each piece? (twelfths – Why?)
How many twelfths are shaded?
Three quarters equals how many twelfths? - Open the pieces of paper up to align the partitions.
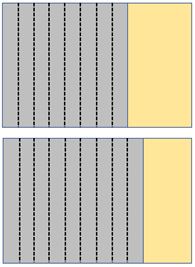
How much greater is three quarters than two thirds? (one twelfth)
You might record 3/4 > 2/3 because 9/12 > 8/12 and ask students to explain the meaning of the symbols. - Slides Two and Three of PowerPoint 1 provide other examples of comparing fractions in the same way.
The Po and Mangu story compares 3/5 and 5/8. Students should realise that both fifths and eighths can be equi-partitioned into fortieths.
3/5 = 24/40 and 5/8 = 25/40 so 5/8 is 1/40 greater than 3/5. Some students might use division on a calculator to check the comparison. 3/5 = 0.6 and 5/8 = 0.625. This means of comparison might open up a conversation about fractions as decimals.
The Thalia and Andreas story compares 2/3 and 7/10. Both thirds and tenths can be equi-partitioned into thirtieths. 2/3 = 20/30 and 7/10 = 21/30 so 7/10 is greater by 1/20. The decimal conversions are 2/3 = 0.6666... and 7/10 = 0.7. - Let students work on Copymaster 1, either individually or in pairs. Look to see that students can make comparisons symbolically and diagrammatically. Roam the room to see that students are converting fractions to equivalent forms to solve the problems and creating diagrams that match their calculations. After a suitable time, gather the class and discuss the solutions.
Session Two
- Write the words “equivalent fractions” on the board.
When we say that two or more fractions are equivalent, what do we mean? - Invite ideas with the aim that students recognise that equivalent fractions are different names for the same quantity.
Do you know any pairs of equivalent fractions already? - Make a list of three pairs offered by students. For example:
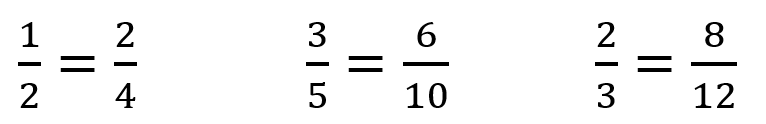
What patterns are true for all three pairs?
Students might notice that there is always an equals sign. What does that symbol mean?
Some might notice that the numerators and denominators are multiplied by the same number, e.g. by four in the pair 2/3 = 8/12.
What does the multiplication mean? In the example, four times as many twelfths fit in one as thirds, so four times as many twelfths fit into the same space as two thirds. - Direct your students to practise converting fractions using the examples on Slide One of PowerPoint 2. You might print out that page for students who find board to page translation difficult. Allow calculator use for students who do not know their basic facts, and consider using collaborative grouping and/or a teacher led group for increased student support. Answers are on Slide Two. Note that the last four examples have a range of solutions. One correct answer is given.
- Slide Three shows the following “Hay There” problem. The type of division is quotative or sharing.
Three goats share two hay bales equally. Each goat gets the same amount.
Six sheep share four hay bales equally. - Which animal gets more hay, a goat or a sheep?
- Let students attempt the problem in pairs and discuss what they notice. Bring the class together at a suitable time and share answers. Discuss:
How could we record the problem using a diagram? (Students often draw lines connecting animals and bales)
How could we record the problem using symbols? Sharing can be represented by division; 2 ÷ 3 = 2/3 (goats) and 4 ÷ 6 = 4/6 (sheep). Do your students recognise that two thirds of a bale is equivalent to four sixths of a bale? The shares are equal since 2/3 = 4/6. - Slides Four and Five of PowerPoint 2 provides other quotative contexts.
Work through each problem with your students. Let them attempt the problem first before sharing strategies.
Students may get confused by which number is the divisor in the kiore and heihei problem. Three kiore sharing four kumara should be represented as 4 ÷ 3 = 4/3 = 1 1/3.
Nine heihei sharing 12 kumara should be represented as 12 ÷ 9 = 12/9 = 1 3/9.
Since 1/3 = 3/9 the shares are equal.
Shares for the kotare and kiwi are as follows:
4 ÷ 5 = 4/5 (kotare) and 9 ÷ 10 = 9/10 (kiwi)
A qualitative judgement is needed to establish that kiwi get more worms each.
4/5 = 8/10 so kiwis get 1/10 of a worm more than kotare. - Provide students with Copymaster 2 to work from in pairs. Roam the room and look for students to:
- Use division to work out equals shares
- Compare the shares using equivalent fractions
- Share, discuss, and justify their thinking with a partner.
- After a suitable time, gather the class to share solutions. The answers are:
- 3 ÷ 6 = 3/6 = 1/2 4 ÷ 8 = 4/8 = 1/2
The shares are equal. - 10 ÷ 6 = 10/6 = 1 4/6 = 1 2/3 15 ÷ 9 = 15/9 = 1 6/9 = 1 2/3
The shares are equal. - 12 ÷ 8 = 12/8 = 1½ 8 ÷ 5 = 8/5 = 1 3/5
Albatrosses get more, 1/10 of an oyster more. - 9 ÷ 12 = 9/12 = 3/4 5 ÷ 9 = 5/9
Goats get more, 7/36 of a bale more. - Any fraction equivalent to 4/5 works, if the denominator is greater than 15.
4/5 = 16/20 = 20/25 = 24/30 etc. - 5 ÷ 8 = 5/8 so any fraction equivalent to 5/8 works.
5/8 = 10/16 = 15/24 etc.
- 3 ÷ 6 = 3/6 = 1/2 4 ÷ 8 = 4/8 = 1/2
Session Three
- Begin the session by creating a number line using equal lengths of tape (adding machine tape is ideal). Start by creating the space between zero and one, then continue to include two and three on the whiteboard.

Where does the number one half live on the number line?
Be aware that some students may think you mean one half of the whole line, i.e. one half of 3 or 1 ½. This common issue is about confusing 1/2 as an operator with 1/2 as a number.
How can we locate one half exactly? - Let students estimate the location first then confirm their estimate by folding a strip in half lengthwise and marking where the fold comes to when one end is located at zero.
- Mark the location of other fractions by estimating first then folding strips to locate the fractions exactly. Check that students remember that the numerator is a count of how many parts iterate (copy end on end) to create the fraction. Good fractions to use are:
Three halves (3/2) three quarters (3/4) five quarters (5/4) ten quarters (10/4)
Five eighths (5/8) eleven eighths (11/8) two thirds (2/3) seven thirds (7/3) - Pose this challenge:
You will get a set of cards (Copymaster 3: Set One).
Your job is to draw a line and organise the cards in order along the line.
Students might use a large sheet of paper and glue stick to create their number lines in pairs. - Provide fraction strips or Copymaster 4 (Paper strips) to students.
- Roam as students work on Set One. Provide Set Two for students who complete the initial challenge.
Add these extra fractions to your number line.
Look for students to:- Recognise where two fractions are equivalent.
- Locate equivalent fractions in the same location (arrange vertically).
- Recognise that a fraction with a numerator of zero equals zero.
- Recognise that a fraction with the same numerator as denominator, e.g. 5/5, equals one.
- Work on the fraction set systematically, starting with the most familiar fractions.
- Justify the positions they put the fractions in.
- After sufficient time, gather the class to share number lines.
Which fractions are the hardest to locate? Why?
Is there a way to simplify those fractions so the task is easier? - Discuss looking for a common factor in the numerator and denominator. For example, in 8/12 both 8 and 12 share a factor of four. Dividing both numbers by four gives the equivalent fraction 2/3.
- Finish the lesson with a riddle.
I am a fraction.
I am between two thirds and three quarters.
My denominator is 24.
Who am I? - Student pairs could create their own fraction riddle to share with another pair.
Session Four
Use PowerPoint 3 to introduce the context of orca and dolphin numbers. Slide Three shows these data:
January July Orcas 8 3 Dolphins 16 9 What do you notice about the data?
Students might comment that the numbers of creatures is much less in July compared to January. Why?
Compared to January, what fraction of the total number of creatures were in July?
12/24 = 1/2 so there are half as many creatures in July.
Are the fractions the same for both months?
8/24 (8 out of 24 for orcas) and 16/24 (16 out of 24 for dolphins) in January
3/12 (3 out of 12 for orcas) and 9/12 (9 out of12 for dolphins) in July
Can we simplify these fractions to make them easier to compare?
8/24 = 1/3 and 16/24 = 2/3
3/12 = 1/4 and 9/12 = 3/4
The fraction of orcas is slightly less in July than in January. Perhaps orcas prefer cooler water.- Slide Four shows how the January data can be grouped to form different fractions.
What fractions can you see? Explain where you see those fractions. - Slide Five shows the July data.
Draw a diagram to show how the fractions ¼ and ¾ can be seen in the orca and dolphin data.
Let students draw their own diagram before animating the slide. - Slide Six shows a survey in a different location, Otago Harbour.
Which month has the greatest fraction of orcas in the whole group?
Do students recognise that the fraction of orcas equals three fifths for both months? - Provide your students with Copymaster 5 to work on individually or in pairs. The worksheet applies equivalent fractions of sets. Roam the room as students work to see that they can:
- Express the proportions for each creature as fractions
- Simplify the fractions by re-unitising (finding common factors)
- Compare the fractions for orcas and dolphins using fractions as numbers.
Answers
Kawhia Harbour
January July
Fraction of orcas = 1/2 Fraction of orcas = 1/2
Fraction of dolphins = 1/2 Fraction of dolphins =1/2
Is there a change in the fraction for each creature comparing July to January? Same
Whitianga Coast
January July
Fraction of orcas = 10/25 = 2/5 Fraction of orcas = 4/10 = 2/5
Fraction of dolphins = 15/24 = 3/5 Fraction of dolphins = 6/10 = 3/5
Is there a change in the fraction for each creature comparing July to January? Same
Queen Charlote Sound
January July
Fraction of orcas = 6/24 = 1/4 Fraction of orcas = 4/16 = 1/4
Fraction of dolphins = 18/24 = 3/4 Fraction of dolphins = 12/16 = 3/4
Is there a change in the fraction for each creature comparing July to January? Same
Kaipara Harbour
January July
Fraction of orcas = 10/20 = 1/2 Fraction of orcas = 4/10 = 2/5
Fraction of dolphins =10/20 = 1/2 Fraction of dolphins = 6/10 = 3/5
Is there a change in the fraction for each creature comparing July to January?
The fraction of dolphins increases and the fraction of orcas decreases.
Akaroa Harbour
January July
Fraction of orcas = 4/24 = 1/6 Fraction of orcas = 2/16 = 1/8
Fraction of dolphins = 20/24 = 5/6 Fraction of dolphins = 14/16 = 7/8
Is there a change in the fraction for each creature comparing July to January?
The fraction of dolphins increases and the fraction of orcas decreases.
Hawke Bay
January July
Fraction of orcas = 12/40 = 3/10 Fraction of orcas = 9/21 = 3/7
Fraction of dolphins = 28/40 = 7/10 Fraction of dolphins = 12/21 = 4/7
Is there a change in the fraction for each creature comparing July to January?
The fraction of orcas increases and the fraction of dolphins decreases.
Session Five
- Use the following Figure It Out pages to set independent work for your students. Whilst students work independently, you could use small group teaching to support students who have not yet to develop the foundational understandings necessary to succeed in the independent tasks. Consider choosing one or two Figure It Out activities, and explicitly modelling and explaining how to complete these tasks. You could use the work samples as evidence of student progress on the Achievement Objectives of the NZC and on the Multiplication and Division aspect of the Learning Progressions Framework.
- The links take you to teachers’ guide pages with a PDF of the student page/s and answers.
- Number Level 3, Book 1: Page 9, Fun with fractions; Pages 10-11, More fractions and To market, To market; Page 14, Racing to new heights.
- Number Level 3, Book 2, Pages 23, On the trail.
- Number Level 3, Book 3, Pages 22-24, Fraction Frenzy.
- Number Sense and Algebraic Thinking, Level 3, Book 1, Pages 18-20, Fraction Tagging.
Extension
- Number Level 3-4, Book 1: Pages 4-5, Stretch and Grow; Page 9, Bean Brains.
Dear parents and caregivers,
This week we are learning about equivalent fractions that are different ways to represent the same amount. For example, one half (1/2) of a birthday cake is the same amount as two quarters (2/4) or four eighths (4/8). We can write the equivalence as 1/2 = 2/4 = 4/8.
Ask your student to explain how he or she compares the size of two fractions with different denominators. For example, “Which fraction is greater: 2/3 or 3/4? How much greater?”