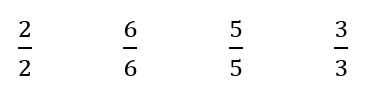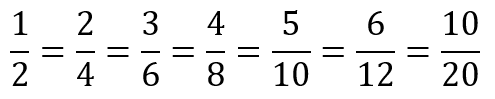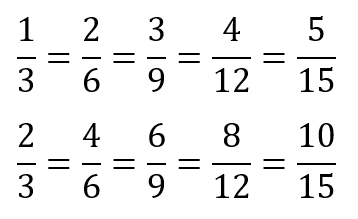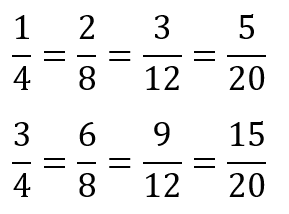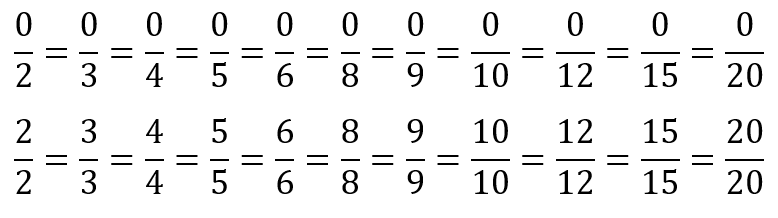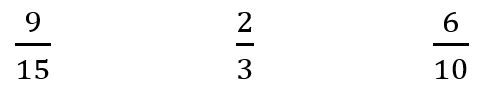Getting partial to fractions

Session one

This session begins with a lesson created by Thomas Kieren, a distinguished Canadian mathematics educator. You will need many strips of paper that are the same length as a standard ruler (30cm). Also have a strip that is 48cm long but has the same width.

1. Begin by asking the students how a strip might be folded in half to make two halves. This will seem trivial as symmetry is natural.
   How do I know that these parts are halves? (Equal parts, all the strip is used, two parts)
2. Provide a couple of non-examples by folding other strips into parts that are not equal, or not all of the strip is used. 
   What is true if the parts are truly halves?
   Look for students to say that one is cut into two equal parts. Fold a 48cm strip into halves.
   Are these parts halves? Why are they a different size to the other halves?
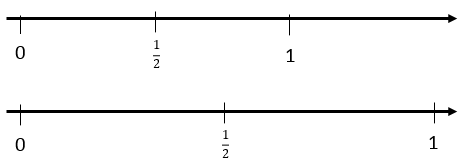
   The important point is that the unit of one determines the size of the halves. Use the half strips to draw two different number lines to represent the relationship of one half to one (whole).
   
3. We are working with fractions as numbers. To do this we need to think about all ones as being the same size. That is very important.
   Where would the fraction 2/2 (or two halves) be on the number line? 
   Where would fraction 5/2 (or five halves) be on the number line? 
   The important point is that non-unit fractions are located by repeatedly joining unit fractions. Five halves are made of five units of one half.
4. Set your students the task of investigating fractions using the paper strips:
   You all know how to fold a strip of paper in two equal parts and call those parts halves. How can you fold one strip into three equal parts? How can you fold one strip into five equal parts?
5. Let your students experiment with developing an equal partitioning method for thirds and fifths. Share their strategies. Students might:
   • Use a ruler to measure the length of the strip then use division to create equal parts. (Is it possible to fold the parts without measuring?)
   • Use one half as a benchmark, knowing that thirds are smaller than halves and fifths are smaller again. (Why are thirds smaller than halves?)
   • Overlap the strip as they fold it to produce three or five equal parts.
6. Discuss: If we can fold into halves, thirds and fifths what other fractions can we make by combining these folds?
7. Demonstrate folding into half then half again.
   What fraction parts have I made?
8. Let your students explore combinations of folds for a prolonged time. Stress the importance of labeling the parts that are made and recording the folds that were used.
9. After a suitable time, share the result of the investigation. Of most interest is how the result of repeated folding can be anticipated. For example:
   If you halve first, then third, what fraction parts do you make? (sixths)
   Does it matter if you change the order of folding to thirding then halving? (No)
   How can you record your folding? (e.g. 1/3 x 1/2 = 1/6) Note that x means "of" as in “one third of one half".)
10. Demonstrate how strip fractions can be used to create a number line: line up several strips that have been folded to show different fractions and mark the folded fractions onto one number line. Ask your students to form their own number line locating fractions of their choice. Encourage them to include some fractions greater than one. Make sure that the students collect their fraction pieces in an old envelope for later use.

Session two

1. Today we will explore equivalent fractions.
   What do you think the word equivalent means?
   From everyday life, students may know that equivalents are the same, e.g. equivalent amounts, equivalent methods, equivalent ingredients or medications.
2. Have students put these fractions in order from smallest to largest.
    
   Do your students recognise that the fractions are all names for one (whole)?
   You may need to make each fraction using a student’s strips from the previous session.
3. Ensure that students understand that these fractions are all on the same spot as one on the number line.
   What other fractions also equal one? 
   What is the same about all fractions that equal one? (The numerator and denominator are the same)
4. Provide the students with copies of page one of Copymaster 1. Alternatively, you could use commercial fraction strips if you have them.
   What equivalent fractions can you see on this page?
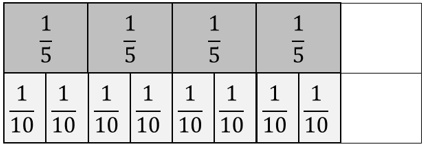
   Students should notice that there are three fractions equivalent to one half. Record their observations as an equality, 1/2 = 2/4 = 3/6 = 4/8. 
   Imagine that tenths and twelfths were on the sheet. What equivalent fractions for one half could you find?
   Students might notice other equivalents to one third and two thirds (1/3 = 2/6 and 2/3 = 4/6) and one quarter and three quarters (1/4 = 2/8 and 3/4 = 6/8).
   The fifths do not seem useful to find equivalent fractions. Why is that? 
   Do you notice any patterns in the equations?
   Students are likely to notice doubling of both numerator and denominator without fully appreciating why that occurs, e.g. 1/2 = 2/4 = 4/8. 
5. Provide the students with page two of Copymaster 1 1 and get them to work through it:
   Find as many examples of equivalent fractions as you can using this Copymaster. You may need to cut out some strips so you can move them around.
   Record what you find as equations and drawings.
6. Give your students an extended amount of time to find examples and record. Look for your students to:
   • Show understanding that non-unit fractions are combinations of unit fractions.
   • Identify fraction pairs that might be equivalent by using their multiplication knowledge.
   • Notice relationships between the numerators and denominators of equivalent fractions, e.g. doubling/halving, trebling/thirding, etc.
7. After a suitable period, bring the class together to discuss how all the possible equivalent pairs can be found. A systematic method is to begin with the smallest denominators (largest pieces) and work down Copymaster 1 in sequence. Record the results in order:
   • Halves:
     
   • Thirds:
     
   • Quarters (excluding fractions with halves and thirds):
     
   • etc...
8. Students might forget to include equivalent fractions for zero and one:
   
   Is there a way to anticipate if fractions are equivalent, without using fraction pieces?
9. Students are most likely to identify the relationships between numerators and denominators. You might record some examples:
   
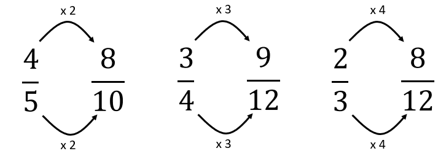
10. It is important for students to understand the reason why the patterns occur. Make sure that a strip model of each equivalence is available, and support students to relate symbols to quantities. For example, for the equivalence 4/5 = 8/10:
                  
     
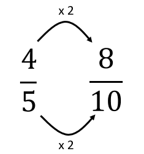
    When four is doubled to give eight, what does this mean? (There are twice as many parts in eight tenths, than there are in four fifths)
    When five is doubled to give ten, what does this mean? (There are twice as many tenths in one as there are fifths. Tenths are half the size of fifths)
11. Look at Videos One, Two, and Three. For each video, ask your students to fold and shade paper strips, as directed. Discuss the final questions:
    What fraction part can you see?
    How many of those parts are shaded?
    Which two fractions have you found to be equivalent?
12. Finally, begin with folding and shading a non-unit fraction, like three fifths or two thirds.
    If you fold the fifths/thirds in half, what sized parts do we make?
    How many of the pieces are shaded? 
    How do you write an equation to represent what we’ve found?
    What happens if you fold the fifths/thirds into other numbers of parts? What equivalent fractions can you make?
    Can you make fifths into hundredths? How? What about thirds?
13. Finish the session with this challenge:
    Put these fractions in order from smallest to largest.
                         
    Ask students to solve the problem first then check their answer using fraction strips. Have them explain their strategy to a classmate.

Session three

In this session students explore ordering fractions and finding the difference between two fractions. Difference can be found either by subtraction or adding on. Students should come to understand that both strategies yield the same result. The length model is used again.

1. Begin with this problem (Using PowerPoint 1):
   Which is more, one third or one half of the same submarine sandwich?
   How much more?
2. Ask students to anticipate the difference between the fractions, one half and one third. They can check their answer using fraction strips, or you can use slide two of the PowerPoint to illustrate the difference of one sixth.
   Why is the difference one sixth?
   Students should notice that 2 x 3 = 6, the connection between the denominators. However, the important understanding is that sixths work because both fractions can be renamed into equivalent fractions with that common denominator.
   How many sixths is one half equivalent to?
   How many sixths is one third equivalent to?
   Could we use twelfths instead? What would be the difference then?
   The difference can be one sixth or two twelfths. Is it strange to get different answers?
   Students should notice that one sixth and two twelfths are equivalent fractions so both answers are different names for the same number. Slide three shows different ways the problem can be expressed as an equation. Discuss what each equation means, e.g. “One third and how much more equals one half?”
3. Move on to the other problems in PowerPoint 1. The problems get more complex as the difficulty of renaming increases. Let your students work in small groups to solve the problems in the most efficient ways they can. Allow access to fraction strips to check answers, and to justify why the answers are correct.
4. After the four examples, hold a short plenary about finding the differences by subtraction.
   I have a new problem. 
   What is the difference between two thirds and five eighths of the same submarine sandwich?
   Where should I start?
   Students should suggest that a common denominator is needed because the parts are different sizes.
   What common denominator will work?
   Hopefully, students suggest 24 using 3 x 8.
   Can two thirds be renamed as so many twenty fourths? How many?
   Can five eighths be renamed as so many twenty fourths? How many?
5. Capture their ideas in symbolic form to create a ‘paradigm example’ of how to subtract fractions.
   
6. Provide your students with Copymaster 2 and ask them to work individually or in pairs to solve the problems. Access to fraction strips will provide some support for students, though some differences are outside the range of the fraction pieces. Look for your students to:
   • Recognise that differences can be found by subtraction, or by adding on;
   • Know that common denominators are needed if the denominators of the two fractions are not equal;
   • Rename one or both fractions as equivalent fractions to enable subtraction;
   • Systematically record their calculations, as above;
   • Represent part-whole relationships as fractions in Question 2, e.g.  120/160 = 3/4;
   • Recognise that pie charts are proportional representations of frequency data, and that comparison of categories can be made using fractional differences.
7. After a suitable time, gather the class to discuss their solutions. Emphasise the relationship between difference and subtraction, and the importance of applying equivalent fractions with common denominators.

Session four

In this session students explore how to add fractions. They learn to recognise when one or both fractions in an addition operation need to be renamed.

1. Use PowerPoint 2 to introduce this problem:
   Tieri’s parents pay for two credits each week so she can play her favourite computer game.
   She is careful not to use all her credits up in one day.
   On Saturday Tieri used up three quarters of a credit. She used another three quarters of a credit on Sunday.
   How much credit does she have left for the rest of the week?
2. Let your students work out the answers in pairs then share strategies with the class. Use the fraction strips made in earlier sessions to model strategies students suggest. Possible strategies might include:
   • Subtracting three quarters from each full credit leaving two lots of one quarter of a credit. The two quarters can be added to make one half.
   • Adding three quarters to three quarters to get six quarters. Six quarters equals one and one half so there will be one half left from two whole credits.
   • Naming two as eight quarters and subtracting 8 – 3 = 5, 5 – 3 = 2, to work out that two quarters of a credit is left.
3. Ask: What was it about the fractions in this problem that made it reasonably easy to solve?
   Students might note that only quarters were involved. Change Tieri’s computer credits scenario to five eighths plus one quarter (slide three of PowerPoint 2). Let your students solve the problem in pairs. Watch out for incorrect strategies such as adding numerators and denominators, e.g. 5/8 + 2/8 = 7/16. Use a strip model to represent the problem and use that model to address problems your students have.
   
4. Discuss how changing the fractions affected students’ strategies. Look for students to highlight that the fractions had different denominators so could not be combined in the same way that three quarters and three quarters were. In this case one quarter can be renamed as two eighths then the fractions can be added. Record and ask:
   How many credits does Tieri have left? (nine eighths, which equals one and one eighth)
   Knowing that fractions can only be added if they refer to the same sized parts is very important. The denominators must be the same.
5. Progress to slides four and five of PowerPoint 2 which have these problems:
   Imagine a week in which Tieri uses up two thirds of a credit on Saturday and one half of a credit on Sunday.
   How much credit does she have left for the rest of the week?
   In a week of the school holidays Tieri uses up four fifths of a credit on Saturday and three quarters of a credit on Sunday.
   How much credit does she have left for the rest of the week?
6. Tell the students that they need to be able to justify why their answer is correct using fraction strips as evidence. Look for students to:
   • Recognise that the fractions have different denominators so cannot be added in that form, e.g.  2/3 + 1/2 ≠ 3/5;
   • Rename each fraction with a denominator that is in common, preferably sixths for the first problem, though twelfths will work as well;
   • Model the equivalence of 2/3 = 4/6 and 1/2 = 3/6 with materials for the first problem;
   • Model the equivalence of 4/5 = 16/20 and 3/4 = 15/20 with materials for the second problem;
   • Record the operation in an efficient way, e.g. 4/5 + 3/4 = 16/20 + 15/20 = 31/20.
   • Find the credits Tieri has left by renaming two in terms of the common denominator.
7. To practise addition of fractions students can work cooperatively on Copymaster 3. They may use fraction strips to support them, if needed, though ask predictive questions to encourage anticipation of the result, such as:
   • Will the credits used add to less than one, or more than one? How do you know?
   • What common denominator/s will work? How do you know?

Session Five

In this session students learn to distinguish between problems in which fractions are treated as measures (numbers), and problems in which the fraction operates on another number. Rational numbers (which fractions are a subset of) conform to the same properties as whole numbers when operated with (added, subtracted, multiplied and divided). Recognition of that conformity is a critical transfer for students at Level Four.

1. Begin with the problem on slide one of PowerPoint 3. The Elise and Harry scenario is, "Two thirds of Elise’s pocket money equals three quarters of Harry’s pocket money." 
   How is this possible? 
   Who gets more pocket money each week, Elise or Harry? How do you know?
2. Challenge your students to find many amounts of pocket money for Elise and Harry that would make the scenario true. Allow the students time to explore and record possible amounts. For example, if Elise and Harry both spend $12, how much do they earn each? $12 is two thirds of what Elise earns so she gets $18. $12 is three quartes of what harry earns so he gets $16.
3. As a class, discuss a generalised way to find a fraction of another quantity. For example, three quarters of $12 can be written as 3/4 x 12 = 9. Students often do not connect the meaning of x in whole number multiplication with its meaning, ‘of’, as in “three sets of four.”

4. Organise the solution data in a table, such as:

   Elise’s weekly pocket money (e)	Harry’s weekly pocket money (h)
   $18	$16
   $81	$72
   $45	$40
   $9	$8
   etc.	etc.

5. Ask: Do you see any patterns in the table?
   Students might notice that Elise’s amounts are multiples of nine and Harry’s amounts are multiples of eight.
   What operations change Elise’s amounts into Harry’s amounts?
   Try dividing Elise’s amounts by nine. What do you notice?
   Students might see that dividing Elise’s amounts by nine then multiplying the result by eight gives Harry’s amount. High achieving students can be encouraged to express that relationship algebraically (8/9 e = h or e = 9/8 h).
6. Work through the other slides in PowerPoint 3 to support students to develop an algorithm for multiplying a fraction by a whole number. With each problem record the calculation, e.g. 4/5 x 15 = (15 ÷ 5) x 4.
7. Provide the students with paper strips and rulers. Cutting an A3 sheet lengthwise with a width of 2 cm is a good size of strip. The final slide of PowerPoint 3 has three challenges for students to solve, individually or in small groups. Look for students to:
   • Recognise that the common denominator for thirds and eighths is twenty fourths, so make the strip a multiple of 24cm long (Challenge One);
   • Recognise that equivalent fractions of the same length are at the same location (Challenge Two);
   • Accept that neither the length of the whole or what fraction of this length is at 18cm are known, but work with the scenario to identify these variables. FOr example, if 18cm is one quarter then the whole strip is 4 x 18 = 72 cm long.