Fraction Tagging

In this activity, students use a fraction wall to compare equivalent fractions and then find fractions of numbers. The 1 whole is assigned different values on different walls, which develops the concept that fractions are measured relative to 1 whole and the value of the fraction depends on the size of the whole. This is known as re-unitising and is an important feature of proportional reasoning.
This is useful as a follow-up activity for students who have been introduced to finding fractions of numbers using:
• early additive part–whole strategies (stage 5), such as deriving from known addition facts, for example: 1/3 of 15 = 5 because 5 + 5 + 5 = 15
• advanced additive part–whole strategies (stage 6), such as using repeated halving or known multiplication and division facts, for example:
1/4 of 48: half of 48 is 24; half again is 12
1/4 of 48: I know 4 x 10 = 40 and 4 x 2 = 8, so 4 x 12 = 48 and of 48 is 12
• advanced multiplicative part–whole strategies (stage 7), for example:
finding 4/5 of 30 by calculating 1/5 of 30 = 6, then 4 x 6 = 24 or 30 – 6 = 24.

You might like to have the students in a guided teaching group construct their own fraction wall before they start question 1. Give each student 8 strips of paper and challenge them to fold them so that they are divided up into halves, thirds, quarters, fifths, sixths, eighths, and tenths. If the strips are 24 centimetres long, students at stages 6–7 could work out how big each section should be in centimetres by working out 1/2 of 24, 1/3 of 24, 1/4 of 24, and so on.
(They may need a calculator to work out the fifths and the tenths.) The students can then use their own fraction wall to complete question 1.
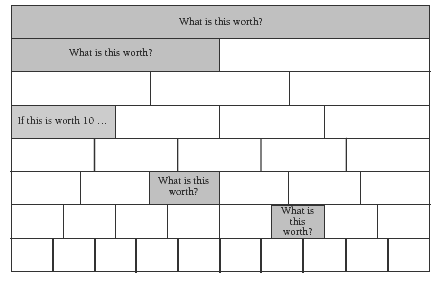
Ensure independent groups understand how the walls work before they do the activity. A good place to start is the wall in question 2. Ask:
What fraction of the top row could 2b be?
How many bricks would there be along the bottom row of this wall if you could see all the bricks in 2d? How do you know?
The students may say:
“The 3 bricks are nearly the same size as 1 brick in the thirds row. That’s 3 x 3 = 9, and 1 more would fit, so that’s 10.”
“I could see 3, and I estimated how many more would fit along the row.”
“It’s the same size as the bottom row in the next fraction wall, and there are 10 in that row.”
So what fraction of the top brick is 2d? How do you know? (7/10. The other part is 3/10, and 3/10 + 7/10 = 10/10, which is 1 whole.)
For the guided teaching group, use the questions above to help the students to use the walls for questions 2–4. Students working at stage 5 may need counters to share into equal groupson the fraction wall if they don’t know a relevant addition fact. Length models constructed from 10, 15, and 24 multilink cubes would be very helpful.
Encourage the students at stage 6 to look for facts they know that could help them, for example:
You’re trying to find 2/3 of 24. What do you know about the 3 times table and 24 that could help?
You’re trying to find 3/5 of 15. What do you know about the 5 times table and 15 that could help?
Encourage students at stage 7 to use multiplicative strategies, such as finding one part first and multiplying that by the number of parts required. Ask:
You’re trying to find 3/5 of 15. Could you find out what 1/5 of 15 is first?
How could you use that to find 3/5 of 15?
Students need to understand iteration of a fraction unit, for example, 3/4 is  1/4 + 1/4  + 1/4 and 4/5 is  1/5 + 1/5 + 1/5 + 1/5.
For question 5, make sure that the students choose numbers for the tops of their walls that are possible to solve using the strategies they know. (Finding of 17 is very difficult to do!) Possible questions and student ideas are:
When you were working out the 24 wall, which fractions were easy to find? Which were harder?
“The fractions with numbers that divide evenly into 24 were easiest, like halves (÷ 2), thirds (÷ 3), and sixths (÷ 6). The fractions that didn’t go evenly into 24 were harder, such as the tenths, because we had to use decimal fractions.” (This connects to factors. That is, 2, 3, 4, 6, 8, and 12 are factors of 24.)
Would it have been easy to find 1/6 of 10? Why or why not?
“No. It’s really hard to divide 10 by 6 in your head.”
Why do you think the numbers 10, 24, and 15 were chosen for the walls in the activity?
“Lots of other numbers will divide into them, especially the 24.”
What other numbers could you choose for the top of your wall so that your classmate could work out the answers in their head?
“I could choose numbers like 12, 18, 20, 30, 32, and 36.”
The a brick on each wall is always half. So why was it worth 5 on wall 2, 12 on wall 3, and 7 1/2 on wall 4?
(This question promotes algebraic thinking.)
“It depends on how much the whole is worth; the half bricks are worth different amounts because the whole brick on the top of each wall is worth different amounts on different walls.”
Can 1/4 of a number ever be bigger than 1/2 of another number? Give me an example.
“Yes. 1/4 of 40 = 10, but 1/2 of 12 is only 6.”

Extension

Students could make up and solve fraction walls where the clue number is on a different brick from the “1 whole” brick, for example:

Answers to Activity

1. a. i. 4/8
ii. 1/2
iii. 2/4
iv. 3/6
b. i. 4/6
ii. 3/4
iii. 8/10
iv. 5/10
2. a. 5. (1/2 of 10)
b. 5. (1/2 or 2/4 of 10)
c. 2. (1/5 of 10)
d. 7. (7/10 of 10)
3. a. 12. (1/2 of 24)
b. 16. (2/3 of 24. 1/3 is 8, so 2/3 is 16.)
c. 12. (2/4 or 1/2 of 24)
d. 20. (5/6 of 24. 1/6 is 4, so 5/6 is 20.)
e. 9. (3/8 of 24. 1/8 is 3, so 3/8 is 9.)
f. 2.4. (1/10 of 24)
4. a. 7 1/2 or 7.5. The row is divided into 2 equal parts, so, a is half of 15.
b. 5. The row is divided into 3 equal parts, so b is 1/3 of 15.
c. 9. The shaded area is equal to 3 out of 5 parts (3/5 ). 1/5 of 15 is 3, so 3/5 is 9.
d. 4.5 or 4 1/2. The shaded area is equal to 3 out of 10 parts (3/10 ).
1/10 of 15 is 1.5 or 1 1/2, so is 4.5 or 4 1/2.
5. Problems will vary.