This unit introduces students to equivalent fractions. Unlike whole numbers that occupy a unique position on the number line, there is an infinite set of fractions that represent the same value. Fraction that are of equal value are said to be equivalent.
- Put fractions on a number line in their correct position in relation to zero and one.
- Show that equivalent fractions occupy the same place on a number line.
- Rename fractions as many equivalent fractions.
- Know how to find equivalent fractions of a set.
Fractions are an extension of the number system beyond whole numbers so that division answers are possible. For example, equally sharing 3 objects among 2 people is only possible if halves are created. In this unit students deal with the complexity of a whole (one unit) that is composed of a given number of parts. The ‘sets’ model of fractions presents conceptual challenges for students as they need to create units and think with those units (described as re-unitising by Lamon, 2007). Fractions of a set inevitably contain different ones, the individual objects a part is made from, and the one that is the whole.
For example, consider a unit of one (the whole) that is made from 12 cubes. One third of the whole is composed of 4 cubes, since 3 lengths of 4 cubes make the whole.
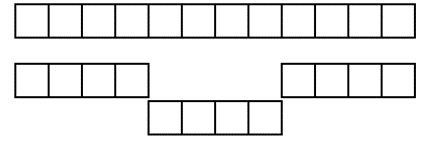
The whole (one) is made of individual cubes but so are the thirds. To see the parts as thirds a student needs to conceptualise them as such, in relation to one. Defining one as invariant (unchanging) is needed in the creation of a number line to show the relative size of fractions. If the length of 12 cubes is called one, then the place of the thirds fractions is found relative to that whole.
The sets model becomes more complicated when the whole is varied. For example, consider these two sets of 12 objects and 20 objects. Both sets have three quarters of the objects shaded.


Three quarters represents the relationship between the shaded part and the whole of each set. Realising that the relationship is the same though the number of objects is different presents a significant conceptual obstacle yet is essential to students’ understanding of ratio. Notice also that equivalence of fractions takes on new meaning in a sets model. 9 twelfths of the left-hand set and 15 twentieths of the right-hand set are shaded. Writing 9/12 = 15/20 is a way to say that the relationship of shaded part to whole is the same for both fractions. Both fractions are equivalent to 3 quarters requires reunitising individual circles as quarters of the whole.
The learning opportunities in this unit can be differentiated by providing or removing support to students, by varying the task requirements. Ways to support students include:
- Providing connecting cubes for students to manipulate when solving problems.
- Modelling how to record fraction symbols and drawing attention to the meaning of numerator and denominator.
- Drawing diagrams to clarify the unit of comparison and the one (whole) in problems.
- Encouraging students to work collaboratively, and to share and justify their ideas.
- Providing enabling prompts, as suggested throughout the unit.
Tasks can be varied in many ways including:
- Alter the complexity of the whole and fractions students work with. Working with halves and quarters tends to be easier than with thirds and fifths.
- Providing 1cm2 grid paper and felt pens to ease the recording demands.
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. The unit uses contexts like fuel gauges on cars, water tanks, mountain biking and kaimoana, that will resonate with most students. Other contexts involving fractions of lengths might also be engaging for your students. For example, the fraction of a race or journey that has been covered at different points is practically useful. Consuming foods that are linear, such as submarine sandwiches, bananas, or sausages, might motivate some learners. Board games, that have a particular number of steps from start to finish, provide opportunities to look at a fraction of a length made of sub-units. Ratios are found in many contexts, such as “What fraction of our class are female?” and “What fraction of the bikes are mountain bikes” and “What fraction of the cows are Jerseys?”
Prior Experience
It is helpful if students have experience with finding fractions of a fixed whole before attempting this unit. Knowing that the numerator is a counter of number of parts and the denominators tells how many of those parts make one, is important to making sense of ideas in this unit.
Units that develop prior experience with fractions are:
Session One
In this lesson students explore names for fractions of length that is divided into a given number of parts.
- Use PowerPoint One, slide 1 to introduce the story.
Have you ever been in a car that runs out of fuel?
What did the driver do?
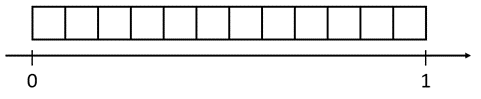
How are cars designed so this should not happen? - Slide 2 shows a fuel gauge. The question is ambiguous as students might talk about the amount of petrol/electrical charge that is left or the fraction of the tank that is left.
What fraction of the fuel tank is left?
Discuss how the fraction can be found.
How many parts is the gauge divided into? (12)
Are the marks in the middle of the parts or at the end of them? (At the end)
What number does E represent? (Zero)
What number does F represent? (One – the whole tank)
What fraction is the arrow pointing to? (About 9/12 or 3/4). - Animate slides 3 to 5 to show how the marks for one half, one quarter, and one third are located. You might like to use a stack of 12 interlocking cubes as a physical representation to supplement the PowerPoint.
What is always true about the size of the parts that the whole tank is broken into? (equal)
What do you think the denominator, bottom number of the fraction, means? (The size of the parts, the number of those parts that make one)
What do you notice about the three fractions? Is there a pattern? (The unit fraction gets smaller as the number of parts increases) - Use slides 6 and 7 to show how non-unit fractions like 2/3 and 3/4 are located by copying (iterating) the unit fraction, just like the marks on a centimetre ruler are located by placing centimetres end on end.
- Slide 8 introduces the use of bar models in other contexts like charge on mobile phones or on the batteries of electric cars.
What does 100% mean?
What does 0% mean?
Explain that percentage is like dividing the bar into 100 equal parts, rather than 12, as you did in the fuel tank example.
What does 75% mean? (Some students might estimate or know that 75% is equivalent to 3/4 since 25% equals 1/4) - Introduce Copymaster 1 and let students work on the problems individually or in pairs. Roam the room to look for the following:
Can students interpret the denominator of a fraction as the number of equal parts?
Do students recognise the numerator as a count of parts the size of the denominator?
Are students able to create correct parts for a given fraction and battery display? For example, 2/5 of ten as 1/5 of ten = 2 bars, therefore 2/5 of ten = 4 bars.
Do students locate the fractions correctly on the number line?
Do they recognise equivalent fractions occupy the same position? - After a suitable period bring the class together to process their answers. Focus the discussion on the points above. Ask students to justify their location of fractions using the bar displays as a diagrammatic reference.
Session Two
In this lesson students come to see that equivalent fractions occupy the same location on the number line. They notice patterns connecting the numerators and denominators of equivalent fractions.
- Show slide 1 of PowerPoint Two.
Why is there a tank on the back of this cottage?
Where is the water collected from?
Rural students or those living on lifestyle blocks will know the importance of collecting and conserving water. Collecting water in tanks may also become more prevalent in New Zealand as water becomes scarce and charges increase. - Slides 2 and 3 begins a story about farmers comparing how much tank water they have left.
Is the female farmer correct?
Do they have more water than the young farmer?
Ask your students to discuss the questions in small groups. They must be able to justify their opinion.
Look for students to explain why the two fractions are equivalent, possibly using diagrams to justify their ideas. Use slide 4 to check the relative size of the fractions.
Focus attention on how the ones (tanks) are of equal size and quarters are found by halving then halving. Twelfths are found by making thirds then partitioning each third into four parts. - Pose two other problems for students to solve in small groups using slides 5 to 8. Let students compare the fractions by drawing their own models before using the answer slide. The comparison of 1/2 and 2/5 shows an inequality since one half is greater.
How much of a full tank is one half greater than two fifths? (One tenth) - Provide each student with Copymaster 2. Let students work in pairs on the problems. Roam the room to look for the following:
Do students interpret the numerator and denominator correctly when shading the fractions of a tank?
Do they write correct equations and inequations?
Can they equally partition one tank into the correct number of parts, by length?
Are their partitions sufficiently accurate to compare the two fractions?
Do they show signs of using multiplication to equally partition, such as ninths are thirds of thirds? - After a suitable time gather the class to share their answers and discuss the points above.
- Use slides 9 and 10 to develop ideas about using multiplication to create equal partitions.
- Slide Nine:
What fractions are made here? (Halves)
If I cut each half in half, what fractions will I have? (Quarters)
If I cut quarters into thirds, like this, what fractions will I have? (Twelfths)
Watch the tank fill. What fraction of the tank is full? (Eight twelfths)
Do eight twelfths have another fraction name? (Two thirds)
Why? (Four twelfths make one third) - Slide Ten:
What fractions are made here? (Thirds)
If I cut each third in fifths, what fractions will I have? (Fifteenths)
Watch the tank fill. What fraction of the tank is full? (Nine fifteenths)
Do nine twelfths have another fraction name? (Three fifths)
Why? (Three fifteenths make one fifth)
- Slide Nine:
Session Three
In this session students explore naming fractions, and looking for equivalence, when the lengths are different. The context of mountain bike riding is used.
- Use PowerPoint Three to provide the focus of the introduction. Use slide 1 to discuss mountain biking.
- Slide 2 animates the rides of two cyclists. You might name the cyclists using students’ names if that is appropriate.
Which cyclist has covered the biggest fraction of their ride?
Students may raise ideas about the length each cyclist has covered. Some may recognise that the bottom rider has completed most of her hill work while the top one has a big hill to climb.
If we just think about the length of their ride, which rider has covered the biggest fraction of their journey?
What makes that difficult to decide? (The tracks are curvy rather than straight) - Animate the slide to show each track divided into kilometre measures.
Does that help you with the fraction of their journey for each biker?
Let students work out the fraction of distance covered (top 12/20 and bottom 8/15). Discuss which fraction is greater. Both fractions are just over one half.
How many twentieths equal one half? (10/20)
How many fifteenths equal one half? (Half of 15 equals 7½ so 7½/15)
Looking at how much more than one half 12/20 and 8/15 are, will be helpful. Since 2/20 (1/10) is more than ½/15 (1/30) the male has ridden the larger fraction. You might use a calculator to show each fraction as a decimal. (12 ÷ 20 = 0.6 and 8/15 = 0.533) - Introduce slide 3 that has a simpler scenario for comparison of riders. The top rider has completed 9 of 12 kilometres and the bottom one 6 of 8 kilometres. Therefore, the fractions are the same, as 9/12 and 6/8 are both equivalent to 3/4. Let students work on the problem in pairs or threes. Roam as they work, looking for:
Do students attend to fractions rather than distances?
Can they name the fractions of each journey?
Do they recognise that both fractions are equivalent? - Gather the class to share ideas. Some students may have difficulty seeing that the fractions are equivalent when the distances are different.
Could each journey be divided into quarters? How? (top: 3km = 1/4, bottom: 2km = 1/4)
How many quarters of their total journey has each rider gone?
Slide 4 shows the comparison when each journey is stretched to the same length, despite the number of kilometres being different. - Let students attempt the problem on slide 5. The top cyclist has ridden 7 of the 15 km and the bottom cyclist 4 of the 10 km. The fractions are 7/15 and 4/10 both of which are less than 1/2.
Both fifteenths and tenths can be joined to form fifths. 3km on the 15km journey equals 1/5 of that journey. 2km on the 10km journey equals 1/5 of that journey. Therefore, 7 out of 15 is 1/15 more than 2/5 and 4 out of 10 is equivalent to 2/5.
Some students may use a rate to solve the problem. 15km is one and one-half times 10km. The bottom rider has travelled 4km and would be expected to travel 1 ½ x 4 = 6km to have the same fraction of a 15km ride. - Introduce the following investigation.
Create two strips of paper of different lengths, say 15cm and 20cm.
Imagine that these two strips are the length of two different bike rides. I am going to shade in a fraction of each strip to show where the rider has got to.
Use the ruler deliberately to shade 9cm of the 15cm strip and 12cm of the 20cm strip.

Which rider has travelled the bigger fraction of their journey?
How could we figure that out?
Students might observe that the rider in the lower strip has travelled further but they also have further to go. Other might suggest measuring each strip and the length of the shading. The fractions are 9/15 and 12/20 which are equivalent. Look for students to suggest grouping the 15ths and 20ths into fifths or using a calculator to convert the fractions to decimals (Both 0.6). - Your challenge is to make up two different lengths strips and shade in a fraction of each strip to show how far the rider has travelled. Once you create your strips, give them to a classmate to find which strip has the longest fraction shaded. Of course, the fractions could be equivalent.
- Let students work with paper strips, rulers, scissors and felt pens to create their strips. Roam the room to encourage students to create lengths that have many factors, such as 24cm, 30cm, 36cm and 48cm since those lengths are easier to partition into familiar fractions.
Session Four
In this session students apply the concept of equivalent fractions to problems with sets of objects. Cooperative logic problems are used to engage students in small group collaborative work. Each group will need three paper plates and a set of interlocking cubes (preferably) though counters will also suffice.
- Use PowerPoint Four to introduce the lesson. The first four slides introduce a co-operative logic puzzle.
There will be four clues and we need to get them all correct to solve the puzzle.
Slide 1 gives the number of shellfish on each plate (12 and 20). It is easy to match the clue by putting on objects to represent shellfish. - Slide 2 states that the fractions of mussels and oysters are the same on each plate.
What fractions would work for that clue?
Let students discuss possibilities, such as one half and one half, one quarter and three quarters.
Are they the only possible fractions? How do you know? - Slide 3 provides a clue about the comparative numbers of mussels and oysters on each plate.
What numbers of mussels and oysters work on each plate?
Students may use trial and error to find 1 + 11= 12 and 5 + 15 = 20 satisfy the clue.
Which plate is correct? How do you know?
Students should recognise that only the plate with 20 shellfish matches one of possibilities for fractions found from slide 2.
Have we got enough information to complete the puzzle? - Let students discuss that question in pairs. Students should know that the 12-mussel plate can be completed because 3 oysters and 9 mussels match the one quarter and three quarters condition.
- Show slide 4 to see if their solutions match the final clue. Since both plates have a ratio of one quarter to three quarters the combination of plates has the same ratio. Note that would not be true if the fractions on the different plates were not the same.
- Use slide 5 as a cooperative puzzle for the students to work through in team of four. Students will need cubes to represent the mussels and oysters and paper plates to organise the cubes. Roam as students work. Look for the following:
- Do students use the materials to organise the information?
- Do students prioritise the clues in order of significance?
- Do students check that all the clues are satisfied?
- Gather the class after a suitable time to share answers and strategies. Solutions is 10 mussels and 5 oysters (left plate) and 9 mussels and 6 oysters (right plate).
What fraction of the shellfish on the left plate are oysters (tia)? (One third)
Which clue card did you use first? Why?
Were any of the clues not needed?
Run though all the clues to ensure the solution is correct. Ask students to justify that their solution meets each condition. - Copymaster 3 has three different cooperative logic problems for students to solve in teams of four. Ideally the cards are laminated and cut up into sets though paper versions work fine. Let students work on one set, and correctly answer that set before getting another set. Roam the room to support students where needed. Encourage recording to hold the information from the clue cards and the use of cubes and plates to trial possible solutions. Remind students where needed that all the conditions must be met.
Solutions are:- Set A Left plate (6 mussels and 4 oysters), Right plate (12 mussels and 8 oysters)
- Set B Left plate (10 oysters and 14 mussels), Right plate (10 oysters and 6 mussels)
- Set C Left plate (16 mussels and 8 oysters), Right plate (27 mussels and 9 oysters)
- Gather the class after a suitable time to discuss strategies to solve the problems. Highlight the importance of understanding that a fraction such as two thirds tells us about the relationship between the number of mussels and oysters, or the relative numbers of shellfish on each plate, but not the numbers of each species or on each plate.
Session Five
In this session students are provided with an opportunity to demonstrate their learning about equivalence with fractions, and how to represent fractions on a number line to judge relative size.
- Introduce Copymaster 4. Work through the instructions slowly so the task steps are clear.
- Let students work on the copymaster individually. Roam the room looking for the following:
- Can students name fractions where the whole is a length (24cm) or a set of objects?
- Can students re-unitise the length or set to name equivalent fractions of the same value?
- Ensure students name their work so you can use the samples for assessment.
- After a suitable time, gather the class and share answers and strategies. If possible, display the copymaster on an Interactive Whiteboard so students can record their answers on-screen. Use the drawing functionality to show positions on the number line and to show groupings of circles on the second page. For example, the shaded circles of this set could represent:

Three fifths (3/5) Six tenths (6/10) Twelve twentieths (12/20) - Pose a final problem for the students to solve in teams of three or four:
What fraction am I?
I am equivalent to a fraction that has four as the denominator.
I have five as my numerator.
Let students work on the problem and share their ideas. Look for them to organise the clues, such as recording the first clue as:
to consider the possible fractions. There are two possible answers 5/10 or 5/20. Either answer is acceptable if it can be justified. - Ask students to create a “What fraction am I?” problem for a classmate to solve.
Dear parents and caregivers,
This week our class have been learning about equivalent fractions that are fractions that look different but represent the same value. For example, one half has an infinite number of fractions equivalent to it, such as 2/4, 5/10, 4/8, 50/100.
We have learned to put fractions on a number line and to find a fraction of a set.
Thanks for supporting our learning.