NA4-9: Use graphs, tables, and rules to describe linear relationships found in number and spatial patterns.
Elaboration on this Achievement Objective
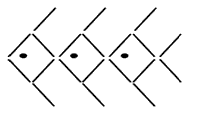
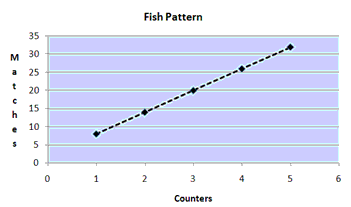
This means students will describe the function rule for a linear relationship as well as recognise recursive relationships where more complex relationships are involved. For example, given the pattern of fish made with matchsticks and counters below, students should be able to represent the relationships in a table and graph and use these representations to predict the terms in the sequence:
 |  |
Counters | 1 | 2 | 3 | 4 | 5 |
Matchsticks | 8 | 14 | 20 | 26 | 32 |
Level Four students should be able to:
- give linear rules connecting the variables (for example, "the number of matchsticks is the six times the number of counters plus two", or "take one off the number of fish, multiply that number by six then add eight")
- extend the graph or table of a linear relationship to predict further co-ordinate pairs, recognising that constant difference (add six in the fish pattern) is associated with points that lay on a line
- use recursive methods to predict further members of a sequence where the relationship is non-linear. For example, the sequence of triangular numbers:
| |||||||||||||||||||||
| +2 | +3 | +4 | +5 | ||||||||||||||||||
Recursive means finding what is added to or subtracted from one term to get the next.
Teaching resources for this Achievement Objective
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra activity from the Figure It Out theme series. A PDF of the student activity is included.
Level Three
Level Four
Number and Algebra
Figure It Out activities
This is a level 3 and 4 algebra strand activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series. A PDF of the student activity is included.
Level Three
Level Four
Integrated
Figure It Out activities
This is a level 3-4 activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Integrated
Problem solving activities
Level Four
Level Five
Number and Algebra
Units of Work
In this unit we are paying close attention to the general rule of a pattern for the first time. We look at odd and even numbers as well as multiples of small numbers. We also look at squares and cubes of numbers and see that it is possible to make more than one pattern from the same three initial...
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand link activity from the Figure It Out series.A PDF of the student activity is included.
Level Three
Level Four
Integrated
Figure It Out activities
This is a level (3+ to 4+) mathematics in science contexts activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series. A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series. A PDF of the student activity is included.
Level Four
Number and Algebra
Problem solving activities
Level Three
Level Four
Level Five
Number and Algebra
This counting collections activity engages students in finding the number of squares of any size on a chessboard.
Level Four
Integrated
This unit provides a set of learning tasks that integrate across the strands of the Mathematics and Statistics learning area of the New Zealand Curriculum and provide opportunities for assessment of student achievement across those strands. Each session may involve more than one lesson, especially...
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series. It also has an achievement objective from the Level 4 Number strategies and knowledge substrand.A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Units of Work
The unit is designed as a simple introduction to systems of linear equations. Students solve problems in which they meet two constraints to find a single solution. Both constraints can be expressed as linear equations.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra activity from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Picture book activities
This is an activity based on the short illustrated novel Fibonacci’s Cows
Level Three
Level Four
Number and Algebra
Figure It Out activities
These are level 3 number problems and level 4 number and algebra problems from the Figure It Out series.A PDF of the student activity is included.
Level Four
Number and Algebra
Figure It Out activities
This is a level 4 algebra strand activity from the Figure It Out series.A PDF of the student activity is included.