This problem solving activity has an algebra focus.
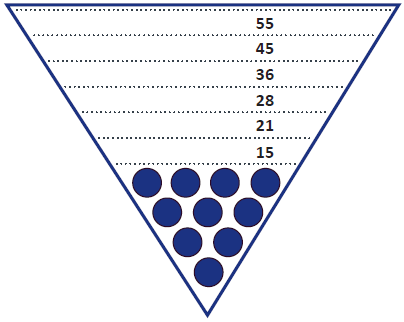
Pharmacists sometimes use a triangular tray to quickly count pills.
You could make a tray like this out of cardboard that can be used to count up to 15 table tennis balls.
Imagine if the tray was larger and the balls were very small.
The 5th number on the tray is 15. The 6th number is 21. The 7th is 28.
What is the 99th number?
- Express rules in words.
- See more than one rule for a given pattern.
- Devise and use problem solving strategies to explore situations mathematically.
This problem is about patterns, how to continue them, and how to find the general term of a pattern. Finding the next term by looking at the recurrence rule, using a table, and incorporating number properties are all valuable skills that can be used in many situations. To successfully solve this problem, your students should have some prior experience with creating tables, noticing patterns in tables, and describing rules for given patterns in their own words. Note that students are not expected to use symbols when describing these rules in this problem.
This problem is one in a series of Algebra problems: Triangular Numbers, Level 3; Square and Triangular Numbers, Level 5; and Triangular Number Links, Level 6. The problems explore triangular numbers and lead to an algebraic formula for the nth triangular number.
See also Building Patterns Constantly and Building Patterns Incrementally, Algebra, Level 3.
- Copymaster of the problem (Māori)
- Table tennis balls or counters
- Copymaster of the problem (English)
The Problem
Pharmacists sometimes use a triangular tray to quickly count pills.
You could make a tray like this out of cardboard that can be used to count up to 15 table tennis balls.
Teaching Sequence
- Introduce the problem to the class. Brainstorm ideas for approaching the problem and keeping track of what has been done.
- Encourage them either to use a table and to see how the entries in the table are related, or to use a geometrical approach. (See Solution.)
- As the students work on the problem in pairs you might ask the following questions to extend their thinking:
What strategies might help you to find the answer?
How can you use your knowledge about numbers here?
Can you see any patterns that might help?
Can you put those patterns into words?
There are further scaffolding questions in the solution. - Share the students’ answers and the provided solutions. Ask them to explain their reasoning. Encourage students to think about both possible approaches (shown below).
Which approach can you understand best? - Ask students to write up a solution.
- Pose the extension problem as appropriate. Perhaps have them begin with a smaller number like 66. Encourage them to use the word rule for triangular numbers that they have found.
- Discuss this with the whole class.
Extension
How many pills will there be along the side of the triangular stack if there are 6216 pills altogether?
Solution
This problem has been solved by a range of simpler methods at earlier levels (see Triangular Numbers, Level 3).
Challenge the students to complete the table (you could leave the third column blank to increase the difficulty). What do they have to multiply by each time in order to go from the term to the triangular number? (The entries in the third column should be, in order, 1, 1.5, 2, 2.5, 3, 3.5, 4.)
What is the pattern for the numbers in the third column? How do they relate to the other two?
How can you now get the third triangular number? The 10th? Can you give a rule for the triangular numbers for any given term? (Take the term and multiply by half of the next term.)
term | triangular number | multiply by? |
1 | 1 | 1 |
2 | 3 | 1.5 |
3 | 6 | 2 |
4 | 10 | 2.5 |
5 | 15 | |
6 | 21 | |
7 | 28 | |
8 |
Help them to see that the number in the third column is half of the next term (4 is half of 8). So the 7th triangular number is 7 x (8/2) = 28. If this is applied to the 99th row of the table we will have to multiply by a half of 100. This leads to a solution of 99 x 50 = 4950.
term | triangular number | multiply by? |
1 | 1 | 1 |
2 | 3 | 1.5 |
3 | 6 | 2 |
4 | 10 | 2.5 |
99 | 99 x (100/2) | 100/2 |
100 | ||
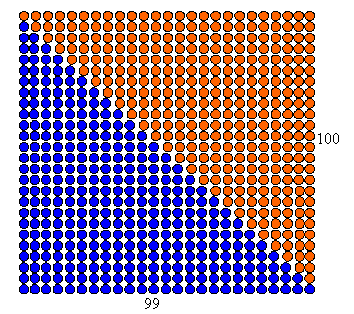
To see this from a geometrical point of view, we can put two lots of the 99th triangular numbers together. Colour one red and the other blue (see below). How big are the sides of the rectangle that is produced? (The rectangle is 99 by 100.) So 2 x (99th triangular number) = 99 x 100. This means that
the 99th triangular number = (99 x 100)/2 = 4950.
Students should be encouraged to express in words the relationships involved. For example, to say,
“a triangular number is the term number x (the next number term)/2”; or
“a triangular number is (the term number x (the term number plus 1))/2”.
Can you see that both of these numbers are the same?
Can you write the expressions using algebra (e.g. using symbols in place of some numbers and the equals sign)? (This is not expected for Level 4 students but some of them might be able to understand it. You will need to use your judgement here.)
Extension to the Solution
There are 6216 pills. This is a triangular number and the term of that number is the length of the side of the pills. So
6216 = (the term number x (the term number plus 1))/2.
This means that:
12432 = the term number x the term number plus 1.
Can you find two factors of 12432 that differ by 1 and that multiply together to give 12432? By experimenting or using square roots you should be able to find that 111 x 112 = 12432. So 6216 is the 111th triangular number.