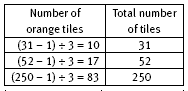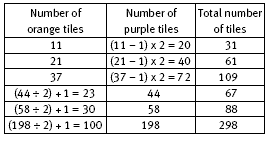This is a level 4 algebra strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (280 KB)
use a table to find a rule for a geometric pattern
write the rule for relationship as a linear equation
FIO, Level 4+, Algebra, Book Four, Bathroom Tiles, pages 8-9
square grid paper
In this activity, students explore short cuts to work out the number of coloured tiles for different tile designs.
In question 1, the students are required to analyse how Lis’s pattern behaves for different numbers of tiles. (Note that she always starts with pink tiles.) The pattern can be thought of as comprising sets of pink and orange tiles (in groups of 3), together with an additional tile. This last tile is always different in colour to the
last set of 3 tiles.
When there are the same number of sets of pink and orange tiles, the equation for the total number of tiles is: total = 3 x number of pink sets + 3 x number of pink sets + 1 pink tile. This number will always be odd and is of the form 6n + 1 (where n is the number of sets of 3 pink tiles).
When there is 1 set fewer of orange tiles than there are sets of pink tiles, the equation is: total = 3 x number of pink sets + [for the orange sets] 3 x (number of pink sets – 1) + 1 pink tile. This number will always be even and of the form 3n + 3(n – 1) + 1 = 3n + 3n – 3 + 1
= 6n – 2
(where n is the number of sets of 3 pink tiles).
In question 1c i, there are 20 sets of 3 tiles, so there are 3 x 10 pink tiles and 3 x 10 orange tiles and the last tile is pink. (Note that the total number of tiles is odd. Using the equation above, we get 6 x 10 + 1 = 61 for the total number of tiles.)
In question 1c ii, there are 37 sets of 3 tiles, so there are 3 x 19 pink tiles and 3 x 18 orange tiles, and the last tile is orange. (Note that the total number of tiles is even. Using the equation above, we get 6 x 19 – 2 = 112 for the total number of tiles.)
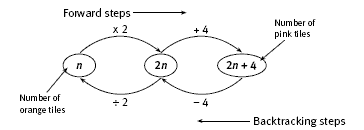
In question 2, there are 2 orange tiles for each set of 4 pink tiles plus an extra block of 4 pink tiles at the end. The orange tiles are always arranged in pairs. The following “backtracking” flow chart is a useful device for determining the number of pink tiles given the number of orange tiles and vice versa. The number of orange tiles is any even number, n. There are twice as many pink tiles as orange tiles, plus a group of 4 pink tiles at the end, so the number of pink tiles is 2n + 4.
The students could use the flow chart in questions 2b and 2c to find the corresponding number of pink or orange tiles and then calculate the total number of tiles.
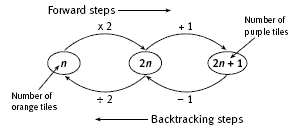
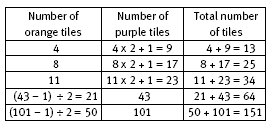
In Bill’s tile designs for question 3, each orange tile can be linked to 2 purple tiles. There is also 1 additional purple tile.
So for a tile section with 100 orange tiles, there are 100 x 2 + 1 purple tiles. For any number of orange tiles, n, there will be n x 2 + 1 = 2n + 1 purple tiles. The total number of tiles is therefore n orange tiles plus 2n + 1 purple tiles. This is n + (2n + 1) = 3n + 1 tiles altogether.
Some of this work requires “reverse” thinking. For example, in question 3d, the students are required to calculate how many orange tiles the pattern has if there are 43 purple tiles. In order to do this, they must reverse the order of calculations used in getting from orange tiles to purple tiles. Instead of multiplying by 2 and adding 1, we subtract 1 and divide by 2. The calculation is then (43 – 1) ÷ 2 = 21. The students might find it helpful to devise a backtracking flow chart to generalise the reverse calculations:
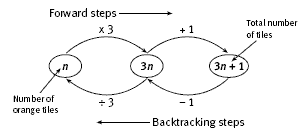
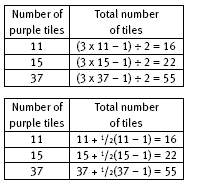
For question 3e, the students will find it helpful to think of the orange and purple tiles as sets of 3. (They may realise this from their table for 3d.) So each orange tile x 3 gives a set of 3 (1 orange and 2 purple). There is always an extra purple tile, so the total number of tiles is the number of orange tiles x 3 + 1. Conversely, the total number of tiles – 1 ÷ 3 gives the number of orange tiles.
The backtracking flow chart below will help the students to complete the first table for 3e:
The second table in question 3e may challenge even able students. There are several approaches to this question, but the reasoning should be along these lines: There is 1 orange tile for each pair of purple tiles and then 1 extra purple tile, so the number of orange tiles equals 1/2 x (the number of purple tiles – 1). One way to find the total number of tiles is to add these quantities. If n is the number of purple tiles, the number
of orange tiles is 1/2(n – 1) and the total number of tiles is n + 1/2(n – 1). As shown in the Answers, another possible rule, where n is the number of purple tiles, is: (3n – 1) ÷ 2. The students should check that this result works (for instance, by using the results of the table in question 3d or by looking at Bill’s designs on the student page).
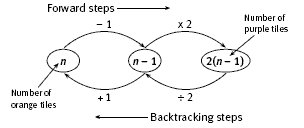
In question 4, each of the orange tiles except the final one is linked to a pair of purple tiles. So when there are 7 orange tiles, there are 7 – 1 = 6 pairs of purple tiles.
When there are 100 orange tiles, there are 100 – 1 = 99 pairs of purple tiles. And when the number of orange tiles is any number, n, there will be n – 1 pairs of purple tiles. So for n orange tiles, there will be 2 x (n – 1) = 2(n – 1) purple tiles. The backtracking flow chart that could be used to help the students with the reverse calculations in question 4c is shown below.
The students might like to see if they can find an algebraic rule that will link the total number of tiles to the orange tiles. Such a rule is: if n is the number of orange tiles, the number of purple tiles is 2(n – 1), so the total number of tiles is:
n + 2(n – 1) = n + 2n – 2
= 3n – 2.
The students might then like to check their results for the table in question 4c.
Answers to Activity
1a.
b.
c. i. 30 pink tiles and 30 orange tiles and an extra pink tile.
ii. 57 pink tiles and 54 orange tiles and an extra orange tile. (37 sets of 3 tiles gives 19 pink sets and 18 orange sets. The last set of 3 tiles is pink, so the extra tile is orange.)
2a.
b. i. 112 tiles. (A design with 36 orange tiles has 19 sets of 4 pink tiles and 18 sets of 2 orange tiles. 19 x 4 + 18 x 2 = 112 tiles)
ii. 298 tiles. (50 x 4 pink tiles + 49 x 2 orange tiles = 298 tiles)
3. a. Bill is correct:
There are 7 orange tiles and 7 x 2 + 1 = 15 purple tiles.
b. For each orange tile, there are 2 purple tiles. There is also an additional purple tile. So for a design with 7 orange tiles, there are 7 x 2 + 1 purple tiles.
c. 87 x 2 + 1 = 175 purple tiles
d.
e.
The total number of tiles is 3 x the number of orange tiles + 1.
Two possible short cuts for finding the total number of tiles are shown in the tables below. They are based on the fact that in each set of 3 tiles, 1 orange tile is half the number of purple tiles. (The total number of purple tiles also includes the extra purple
tile at the end.)
4. a. Answers may vary. A possible short cut is (8 – 1) x 2 = 14. For 4 orange tiles, there are (4 – 1) x 2 = 6 purple tiles, and for 6 orange tiles, there are (6 – 1) x 2 = 10 purple tiles. So if there are 8 orange tiles, there are (8 – 1) x 2 = 14
purple tiles.
b. (47 – 1) x 2 = 92 purple tiles
c. Based on the short cut above: