Family Likeness

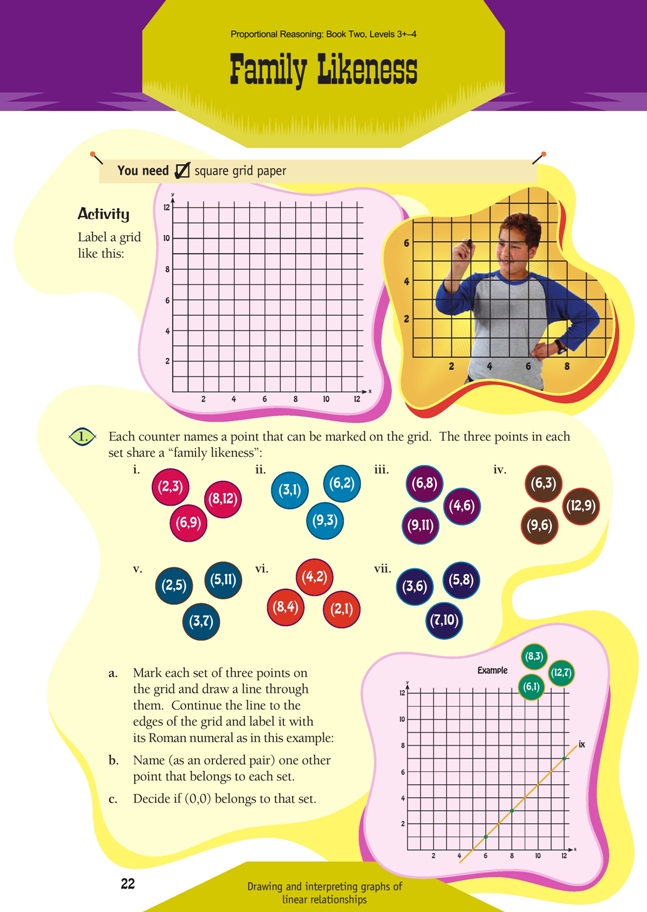
Activity

This activity gives meaning to the notion of a linear (straight line) relationship. It should help students to think of a straight line graph as made up of many points (an infinite number) and to understand that each of those points can be described as a pair of numbers (co-ordinates) that are connected according to some rule (the “family likeness”).
When introducing this activity, get your students to think about its title as a metaphor for the learning outcome (found at the bottom of the page): just as we can often tell that people are related because they have similar characteristics, patterns in numerical data often point to connections. Write the words finding connections on the whiteboard to emphasise the thinking that this activity aims to encourage.
Once the students have plotted the sets of points in question 1, ask them what the lines tell them.
The key ideas are:
• If a straight line can be drawn through a set of points, the points are members of the same “family”.
• All other points on the same line are also members of that family.
• Any points that are not on the line are not part of that family.
Students should also note that the line places the ordered pairs in ascending or descending order based on the number for the x (horizontal) axis. This can be a help in finding the rule that connects the two parts of each pair.
Once the students have drawn the lines in question 1, they should find it easy to name other ordered pairs that belong to the same “families”.
In question 2, students have to try to spot the connection that uniquely links each pair of x and y values in a family. They may find it a help to make a table showing consecutive x values and then enter the matching y values from the graph. A completed table for equation iv would look like this:

Be aware that if students do create tables, they may need to use negative numbers to complete them (as in the example above). But this won’t do them any harm!
Make it clear that the aim in question 2 is to find a rule that connects each pair of x and y values, not an observation about just one of the values. (Not, for example, “the y value goes up 1 each time”.) Give your students every opportunity to discover for themselves how to find the connections.
One way of teaching this idea is to take a single ordered pair and get the group to brainstorm possible connections. For example, possibilities for the ordered pair (9, 6) include:
• “The x value plus the y value makes 15.” [+]
• “The x value is 3 more than the y value.” [–]
• “The y value is 3 less than the x value.” [–]
• “The y value is ⅔ of the x value.” [x]
• “The x value is 1½ times the y value.” [x]
• “Double the x value equals triple the y value.” [x]
When brainstorming possibilities, students should consider each of the four operations: +, –, x, and ÷. Once they have done this, they should take a second ordered pair from the same family and see which of the possible (brainstormed) connections is true for that pair too. If students find that two of their rules work, this will be because both express the same connection in different ways. (In the bulleted list above, 2 and 3 are just different ways of saying the same thing, as are 4, 5, and 6.) Once they have what they think is the correct connection, they should test it on the third ordered pair.
Students should be aware that a connection may involve more than one mathematical operation. For example, the rule that connects the three ordered pairs {(2,3), (5,15), (6,19)} is “multiply the x value by 4 and then subtract 5”.
As they find the rules that connect the x and y value for each set of ordered pairs, students should try to express them as equations involving x and y. Each rule is able to be expressed in different ways, but the differences are cosmetic, not mathematical.
In question 3, students must image extensions to the lines on their graph. By doing this, they will understand that the graph on the page is not a complete picture at all; it is just a small part of a graph that extends outwards off the edge of the page in all directions.
Have the students do question 4 by themselves and then swap their sets of ordered pairs with a classmate. Each should then try and work out the rule that connects the ordered pairs.
By way of extension, you could ask your students to consider the graph they created for question 1 and explain what is going on when two lines cross: which of the two families of points does this particular point belong to? (Both) Get them to check their ideas mathematically, putting the values from that ordered pair into the rule for each line. Is it possible for an ordered pair to belong to even more than two families of points? (Yes) See if they can find such a pair.

Answers

1. a.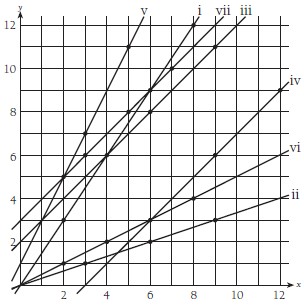

b. Answers will vary.
c. (0,0) belongs to sets i, ii, and vi.
2. Note that these answers can be expressed in different ways:
i. Multiply the first number by 1 to get the second number.
ii. Divide the first number by 3 to get the second number.
iii. Add 2 to the first number to get the second number.
iv. Take 3 off the first number to get the second number.
v. To get the second number, double the first number and add 1.
vi. Halve the first number to get the second number.
vii. Add 3 to the first number to get the second number.
3. (18,6) belongs with set ii; (20,10) belongs with set vi; (14,17) belongs with set vii; (14,21) belongs with set i; (11,23) belongs with set v; (17,14) belongs with set iv; (13,15) belongs with set iii.
4. Answers will vary. Here is one example:
{(0,0), (3,15), (4,20)}