Strawberry Milk

The Problem

Mary the milk lady had a square milk crate that could hold four bottles. In how many ways can she put two strawberry milk bottles into the crate?

Teaching sequence

1. Talk about delivering milk. Ask
   What containers does milk come in?
   How is it delivered? What do the milk bottles travel in?
   How big are milk crates?
   How heavy are they?
2. Talk about Mary delivering milk.
   Why might she have a small crate?
   What shape is the crate? What do we know about that shape?
   How many bottles can she get into her crate?
3. Tell the class Mary’s problem.
   How can you solve the problem?
   What might you need to help you?
4. After some discussion, let the class go into their groups or work alone.
5. Help the children that need it.
6. You may need to call them all together at some stage to see how many arrangements they have come up with. Get them to take turns in putting a picture of one of their arrangements on the board. Call each arrangement by the child’s name who found it (see Solution).
7. Ask
   How do you know if there are any more?
8. Try to get them to see the systematic approach that we used in the Solution to get all possible answers. As this is a new idea for the children, they may not all understand the concepts involved the first time round. In that case, follow up with the Extension problem. This will give them a chance to practice the ideas they have just seen.
9. Let a few groups/children report back to the whole class. Try to choose groups that have used different approaches to the problem. Let the children put their pictures of the bottle arrangements on the wall.
   (The lesson could be stopped here and continued the next day. If so, you will need to go over what you did the previous day and recall the crate arrangements with the children’s names attached. We have provided our own names in the Solution. We use those names in the rest of the Teaching Sequence.)
10. Ask the class
    What happens if you turn Charlie’s crate by a quarter turn?
    Does this give you someone else’s crate? Whose?
    What happens to Hine’s crate if she turns it through a half turn?
11. Then try asking questions like
    If I have just turned the crate through a quarter turn and I’ve got Joe’s crate, whose crate did I start with?
12. Quiz them about the various crates.
    Do any of these crates look the same?
    Do some of them have anything in common?
13. Call crate arrangements that can be rotated into each other ‘alike?.
14. Ask them to go away and put alike crates together.
    Whose crates look alike?
    Whose crates are really different?
    How many different answers are there?
    Try to get them to see that rotating the crate around will move one arrangement to another (see the Solution).
15. Get them to report back on their progress.
16. (This is an optional step that you may want to ignore or only ask of the more able students.) Look at the properties of the arrangements.
    Are there any crates that stay the same after a rotation of a quarter turn?
    Are there any crates that stay the same after a rotation of a half turn?
17. Suggest that they look at the Extension problem again to see if there are any answers that may be alike.
18. Discuss their conclusions.

Extension

Mary found a slightly bigger crate. This one had room for 9 bottles. In how many ways can she put 8 strawberry milk bottles into her new crate?

Solution

It is likely that the students will attempt this problem using a number of strategies. Probably the best things to do are to use a drawing or use equipment. We imagine that, no matter how the children try to do this, they will first of all do it quite unsystematically. This way they will come up with several ways of putting the two bottles into the crate. After thinking about the situation with you and with the rest of the class, they might come up with something like the following.

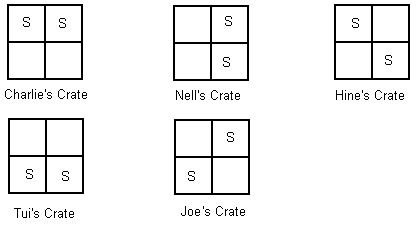
So we have gone through step (i). We have found some answers. The question is, are there any more?

To answer that question we need to be systematic. So let’s think of a way of doing the drawing so that we don’t miss anything. One way to do this is to first put one strawberry milk bottle in the top left-hand corner of the crate and then move the other around the crate from one possible arrangement to the next. This will give us the following possibilities.

(The last crate is new. Perhaps Ye discovered that. So we’ll call it Ye’s crate.)

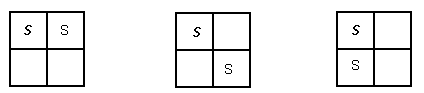
There are only three ways of doing this. We’ve now exhausted all possibilities for a bottle in the top left-hand corner of the crate. So now move on to the top right hand corner.

Here we move the other bottle one place round each time. One thing that we should notice is that the last arrangement isn’t new. That’s because we have put a bottle in the top left-hand corner again. So there are only two new possibilities here. We list them below.

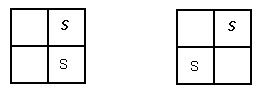
Now let’s put the first bottle in the bottom left-hand corner. This gives us only one new answer. Circling the second bottle around the crate gives arrangements that we have already found.

Any other arrangement that has a bottle in the bottom left-hand corner, forces the other bottle to be in a position we’ve already considered.

Putting the first bottle in the bottom right-hand corner, the only place we haven’t yet started with, again gives us nothing new. This is because the other bottle must be in a position that we’ve already considered. So, by being systematic, we’ve accomplished the last two steps of the problem. We’ve got all possible answers (step (ii)) and we’ve shown that these are all there are (step (iii)).

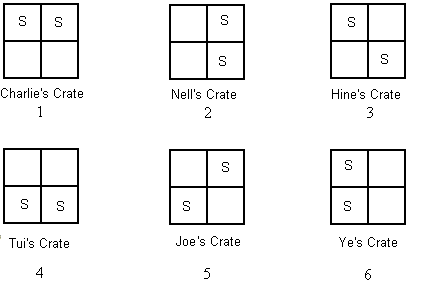
Just for completeness, we list all six possible answers below.

This brings us to the end of Step 9 in the Teaching Sequence.

Do some of the six answers above look the same? Do some of them look different?

When you look a bit harder, 3 and 5 look more like each other than 1, 2, 4, and 6. You see 2 and 5 show bottles opposite each other while in 1, 2, 4, and 6 the two bottles are on the same side of the crate.

But we can take this further. Because Mary’s crate is square, we can rotate it through a quarter turn. In doing that the situation of 3 becomes that of 5. We can rotate the crate so that the bottles in 3 end up in the same position as those in 5. So there is a sense in which we can’t tell the difference between 3 and 5. Call them ‘alike?.

Suppose that Mary put the crate down in position 3 and went off to have a cup of tea. Then suppose that Joe came along and rotated the crate through a quarter turn, it could end up in position 5. But then Hine might rotate it through another quarter turn the other way and it would end up in position 3. Mary would never know that the children had been playing with her crates. So there is a sense in which 3 and 5 are really the same arrangement.

And the same thing happens with 1, 2, 4, and 6. One rotation of a quarter turn will change 1 into 4. Another rotation will turn 4 into 6. Another rotation will turn 6 into 2. Are these four positions really different? All of these are alike.

So we have two groups of ‘alike? arrangements. These are 3 and 5 and 1, 2, 4, and 6. Therefore there is a sense in which there are only two arrangements of the crates and every other arrangement comes from one of these just by rotating the crate. These two arrangements are represented by the non-alike crates of Charlie and Hine.

Extension

In the first part here we consider the steps up to Step 9 of the lesson. We will go straight to finding a systematic way to do the problem and assume that the students have already guessed and checked their way to producing some answers.

The easiest way to be systematic here is to look at where the space without a bottle can be. Just take it systematically round the crate starting at, say, the top left-hand corner of the crate. So what we get below are the only 9 possibilities.

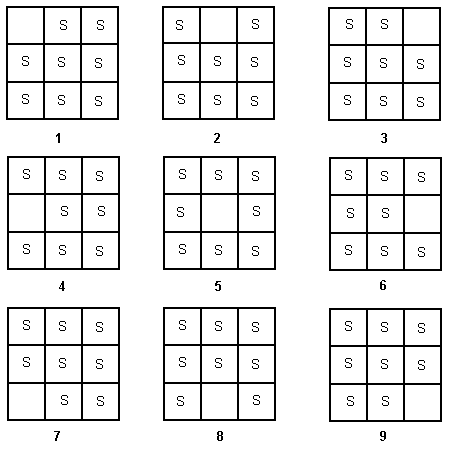
Then consider the notion of ‘alike?.

How many of these crates are different? How can we rotate one situation onto another? First you can see that 1, 3, 7, and 9 can be thought of as being alike. They all have a corner square free. And you can rotate any one of these crates through a quarter turn onto any of the others. In fact if you start with 1 and keep rotating in the same direction, you will get each of 3, 7, and 9.

Second, 2, 4, 6, and 8 are alike. They all have the middle square on a side empty. Again you can rotate from any one of these to any other.

Finally 5 is on its own. It has the centre space vacant. When you rotate it, the centre space stays in the centre. It can't be matched up to any other arrangement.

Then you should notice that there is no way of rotating 1 to look like 2 or 5. And 2 can’t be rotated to look like 5. So we can think of there being three distinct groups of answers under rotation. These are represented by the arrangements 1, 2 and 5.

At this point you might like to go on to Step 15. Look at the properties of the arrangements.

Are there any crates that stay the same after a rotation of a quarter turn?
Are there any crates that stay the same after a rotation of a half turn?

You might also turn the ‘alike? property around and look at it another way. You get the same result as turning the crate, by getting the children to go round and look at the crates from different sides.

If the students seem to be getting a lot of fun and mathematics out of these problems, then vary the number of bottles and see how they go.