This problem solving activity has a logic and reasoning focus.
Miriama is making a square window using 16 smaller red or white square panes.
What is the biggest number of red panes that Miriama can put in the window so that no three of them are in any row or column?
How many ways can this be done?
- Create geometric shapes that satisfy the no three in a line condition on 4 by 4 grids.
- Devise a systematic approach to find possible outcomes.
This problem requires students to use a systematic approach to justify that they have considered all possibilities. The problem also challenges students to recognise the symmetry in a figure, and to see that by rotating a figure, through a quarter turn either clockwise or anticlockwise, two 'answers' are essentially the same. Symmetry through a line in the plane of the square is therefore important.
See also these Logic and Reasoning problems: Strawberry Milk, Strawberry and Chocolate Milk, Level 1; Three-In-A-Line, Level 2; No Three-In-A-Line, Level 3; No-Three-In-A-Line Again, Level 5; No-More-In-A-Line Level 6; and No-Three-In-A-Line Game, Level 6.
- Bottles tops
- Copymaster of 3 by 3 windows
- Copymaster of 4 by 4 windows
- Coloured pens and paper
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
The Problem
Miriama is making a square window using 16 smaller red or white square panes.
What is the biggest number of red panes that Miriama can put in the window so that no three of them are in any row or column?
How many ways can this be done?
.gif)
Teaching Sequence
- Pose Miriama’s problem to the students and check that it is understood.
- After some discussion, have the students work on the problem in their groups. Discuss the different strategies they might use (e.g. recording with a table, guess and check, drawing diagrams).
- As solutions emerge, have students share their ideas and show and explain their arrangements. Give a student's name to each arrangement for convenience in referring to it.
- Ask:
Are all of these arrangements different?
How might we think of some of them as being the same?
How could we systematically find other arrangements that are similar or different? - Pose the extension problem as and when appropriate.
- Have groups report back to the class. Choose groups that have used different approaches to the problem.
- Students could construct their own windows using transparent coloured paper or a digital tool (e.g. Google Slides).
Extension
Miriama is now working on a square window that has 25 smaller red and white square panes. What is the biggest number of red panes that she can put in the window so that no three of them are in any row or column? In how many ways can this be done?
Solution
The method of solution here is the same as for No Three-In-A-Line, Level 3
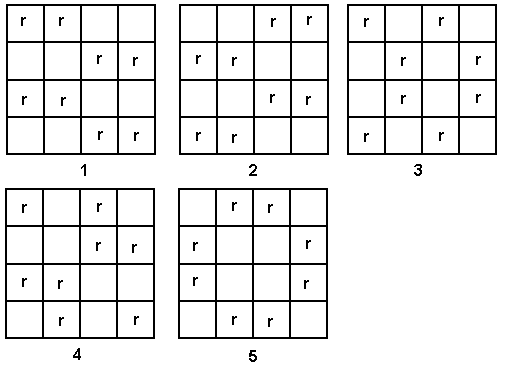
The first thing to note is that we cannot have more than two red panes in each row of the window. This means that we can’t fit in more than 8 red panes without forcing three to be in a row or column. So we can systematically try to insert two red panes in each row to see if that is the largest number of red panes that Miriama can use. Here is the full set of answers:
Note that 1 and 2 are the right- and left-hand forms of the same situation. We can flip 1 over about an axis of symmetry in the plane of the window, so that it becomes 2. Hence for windows these two arrangements are the same. So there are 4 different solutions to Miriama’s problem: 1, 3, 4, and 5.
Solution to the Extension
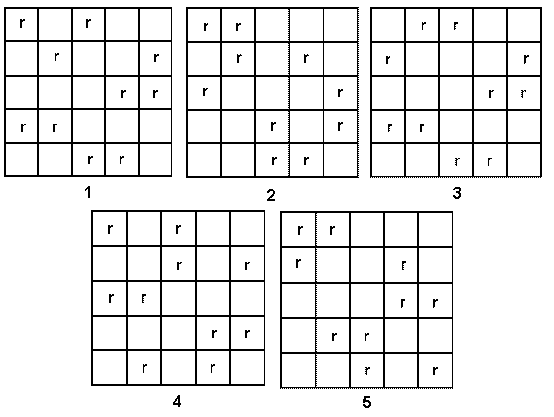
With 25 possible squares we can put at most two red panes in a row so that no three are in a row or column. So let’s try to put 10 red panes in Miriama’s window. This can be done in 5 different ways. Any other way that you can find can be rotated or reflected into one of these 5.