This unit requires students to work with the number of ones, tens, hundreds and thousands in four-digit whole numbers to improve their understanding of them.
- Recognise the importance of zero as a place holder in whole numbers.
- Recognise and apply understanding of the base ten system repeated naming pattern of thousands, hundreds, tens and ones.
- Appreciate that tens are nested in hundreds and thousands and use that knowledge to rename whole numbers.
- Rename whole numbers to make the addition and subtraction of collections of tens or hundreds easier.
Understanding place value is crucial if students are to develop the estimation and calculation skills necessary to become numerate adults. Our number system is sophisticated, though it may not look it. Numerals exist all around us in the environment. The meaning of digits, and the quantities they represent, can be challenging to understand. Our number system is based on groupings of ten. Ten ones form one ten, ten tens form one hundred, ten hundreds form one thousand, and so on. The system continues, giving us the capacity to represent very large quantities. The place values one, ten, one hundred, one thousand and so on are powers of ten. Therefore, the place immediately to the left of a given place represents units that are ten times more than the given place, e.g. thousands are ten times greater than hundreds.
Ten digits - 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 are used to represent all numbers in our base-10 system. We don’t need a new number to represent ten because we think of it as one group of ten. Similarly, when we add one to 999, we write 1000 and do not need a separate symbol for one thousand. The position of the 1 in 1000 tells us about the value it represents. Zero has two uses in the number system, as the number for ‘none of something’, (as in 6 + 0 = 6) and as a placeholder ( as in 7040). The term 'placeholder' means a number occupies a place, or several places, and describes the values represented by the other digits. For instance, the zero in 7040 acts as a placeholder in the hundreds and ones places.
Place value means that both the position of a digit as well as the value of that digit indicate what quantity it represents. In the number 2753 the position of the 7 is in the hundreds column which means that it represents seven hundred. Two is in the thousands column which means that it represents 2 units of one thousand, called 2000.
Understanding the nested nature of place value becomes very important as students learn to operate on whole numbers and extend their knowledge to decimals. Nested means that the places are connected, e.g. within hundreds there are tens, within ones there are tenths. Renaming a number flexibly is an important application of nested place value.
In particular, it is vital that students understand that ten ones combine to form a unit of ten, ten tens combine to form a unit of one hundred, and ten hundreds combine to form a unit of one thousand. For example, the answer to 2610 + 4390 could be represented at 2000 + 4000 + 1000 = 7000, because 610 and 390 combine to form one thousand. Similarly, when a unit of one thousand is ‘decomposed’ into ten hundreds, the number looks different but still represents the same quantity. For example, 4200 can be viewed as 4 thousands, and 2 hundreds, or 3 thousands and 12 hundreds, or 2 thousands and 22 hundreds. Decomposing is used in subtraction problems such as 7200 – 4800 = □ where it is helpful to view 7200 as 6 thousands and 12 hundreds.
At Level 3 students need to develop a multiplicative view of place value that includes understanding the relative size of quantities represented by different numbers. A nested view of 230 as 23 tens allows multiplicative connection between 23 and 230. 230 is ten times larger than 23, and 23 is ten times smaller than 230. Such knowledge can be expressed with equations, 23 x 10 = 230, 10 x 23 = 230, 230 ÷ 10 = 23. Multiplication and division basic facts can be leveraged for harder calculations, 4 x 3 = 12 so 4 x 30 = 120 (ten times more). 30 x 4 = 120 as well. 12 ÷ 3 = 4 so 120 ÷ 30 = 4.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- providing physical materials so that students can anticipate actions and justify their solutions. Place Value People is a representation that is accessible, allows for combining and partitioning units, and can be used with whole numbers up to 4 digits
- connecting symbols with quantities, especially as the quantities are combined (addition), separated (subtraction). Support students to generalise properties that always occur, e.g. in a base-10 system, ten units of a place value combine to make one unit of next highest place value
- using important mathematical vocabulary to discuss concepts, in particular words for the places (ones, tens, hundreds as examples) and words associated with operations, e.g. addends and sum for addition
- encouraging students to collaborate in small groups (mahi tahi relationship) and to share, and justify, their ideas
- using technology, especially calculators, in predictive, pattern-based ways, e.g. What will happen to 234 if you multiply it by ten?..divide it by ten?
- altering the complexity of the whole numbers and operations that are used. You might refer to the Level 2 place value units for some students. Within this, consider the basic multiplication facts knowledge of your students. It may be more appropriate for them to work with digits below 5, if they are confident in their 1-5 multiplication times-tables. To encourage successful participation from less confident students, consider providing calculators to ease the cognitive load needed for working with larger numbers.
The context used for this unit is people which should be engaging for all students. You might want to relate problems to people throughout the world or in regions of Aotearoa, and places relevant to your students, to provide more real-life settings. Encourage students to be creative by accepting a variety of strategies, and asking students to create their own problems for each other to solve. Ideas and strategies can be recorded on digital devices to easily share students thinking with their peers.
Te reo Māori vocabulary terms such as uara tū (place value), poro-tahi (ones block), poro-tekau (tens block), poro-rau (hundreds block) and whakarea (multiply) could be introduced in this unit and used throughout other mathematical learning.
- Calculators,
- Place Value People (made from Copymaster 1)
- Scissors
- Stapler
- Digit cards or ten-sided dice.
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- Copymaster 6
- PowerPoint 1
- PowerPoint 2
- PowerPoint 3
Session 1
This unit builds on the units at level 2 that explore place value of whole numbers to 1000:
- https://nzmaths.co.nz/resource/building-tens
- https://nzmaths.co.nz/content/building-two-digit-place-value
- https://nzmaths.co.nz/resource/building-tens-and-hundreds
You may want to revisit those units or, at least use some of the independent tasks. It is expected that students will develop an appropriate repertoire of basic multiplication facts- either prior to, or during, this unit.
Introducing Place Value People as a model
- Begin the lesson using PowerPoint 1. The first three slides show numbers of people icons. All three collections contain 120 icons. This could be introduced as members of your school (e.g. going to the marae, ordering sausages at lunchtime, going to swimming lessons). The purpose of the class task is to establish that grouping objects helps us to count the number of objects efficiently and that tens-based grouping is the normal convention (though it was not always historically).
What is an efficient way to count the number of people? - Slide One: There are five blocks of 4 x 6 = 24 people. Students may approach the task additively, e.g. 6 + 6 = 12, 12 + 12 = 24 to find the number in each block. 24 + 24 = 48 to establish the total. Try to encourage a multiplicative approach such as 4 x 6 = 24, 5 x 20 = 100, 5 x 4 = 12 so there are 120 people.
- Slide Two: There are three blocks of four tens. The use of place value units makes it much easier to count the 120 people. Look for students to apply multiplicative structure, such as, 4 x 10 = 40, 3 x 40 = 120. Discuss how 3 x 4 = 12 is used to find 3 x 40 = 120.
- Slide Three: The people icons are distributed randomly. Give the students a short time to count the icons since allowing them to continue is non-productive. The point is that counting in ones is time consuming and error prone. The animation creates collections of ten icons that might be used to estimate the total number.
- Show the students Copymaster 1 (place value people). Discuss that the 100 sheet is composed of ten rows of ten people or four groupings of 5 x 5 = 25 people. Slide Four of PowerPoint 1 illustrates how the number 365 can be made efficiently using the Copymaster. Slide Five poses some interesting questions about 365.
- Question One: Within each 100 are ten tens. 300 is comprised of 30 tens. Since 60 is six tens there are 36 tens altogether. Some students may say that the other five is half of a ten or point five. That is correct. The answers of 36 tens and 36.5 tens are correct.
- Question Two: In each ten there are two fives. An efficient way is to double the number of tens to get the number of fives, i.e. 2 x 36 = 72 (add the final five to get 73) or 2 x 36.5 = 73.
- Question Three: To make 365 into 400, five are needed to make 370 and another 3 tens to make 400. 400 plus 100 equals 500. In total 100 + 30 + 5 needs to be added.
What number am I?
Copymaster 2 contains “What number am I?” challenges for the students to solve. The clues involve place value understanding and students are expected to use the Place Value People model to solve the problems if they need to. Look to see if your students:
- Use a systematic approach to eliminating possible numbers as they work through the clues
- Show a sense of quantity by making numbers with the Place Value People model
- Demonstrate nested place value knowledge, e.g. 74 ten equal 740.
Wish-upon-a-digit
A digital form of this game is called Wishball. It can be found at this link.
Students will need copies of Copymaster 1 (Place Value People) and Copymaster 3 (Scoresheets) to play. They will also need a way to randomly generate digits. This could be digit cards to draw from, a 10-sided dice, or an online random number generator.
The goal of the game is to use place value number operations to get from the starting number to the target number in as few turns as possible.
To set up the game:
- Select three digits randomly to form a starting number and mark this on the number line at the top of their recording sheet.
- Select three digits randomly to form a target number and mark this on the number line as well.
For each turn:
- Select a digit randomly.
- Choose whether the digit represents ones, tens or hundreds (for example, a 3 could be worth 3, 30 or 300)
- Choose whether to add or subtract this number from the current running total and record this on the recording sheet.
When it will finish the game you have one opportunity to choose the digit you want (for example, if you were up to 467 with a target of 667, you can choose to have a 2, and add 200 to finish the game).
Session 2
In the following sessions students are expected to apply multiplication and division to place value. They learn how many tens and hundreds are nested in whole numbers to four digits, and the effect of multiplying or dividing a whole number by ten.
Lucy’s Number Trick
- Play the first four slides of PowerPoint 2 to introduce Lucy’s look for a pattern in the 11 x tables with two-digit whole numbers. Let students talk in pairs as each answer comes up.
Is there a pattern?
What is the pattern? - While showing slides 5-7, invite your students to predict the answer to other 11 x facts. Prediction encourages them to conjecture on possible rules. Access to calculators will support students to check their predictions. After slide 7, discuss how the answer might be predicted. In general, for any two-digit number, 10a + b the answer has a ones digit of b (45). The tens digit is a + b (4 + 5 = 9) and the a becomes the hundreds digit. If a + b (9) is less than ten the pattern is easier to spot (45 becomes 495 when multiplied by 11). For example, 11 x 45 has an answer of 5 ones, 4 + 5 = 9 tens, and 4 hundreds (495).
- If a + b is ten or greater, then some renaming occurs. Take 11 x 57 for example. The answer has 7 ones, 5 + 7 = 12 tens, and 5 hundreds. Since 12 tens are 120 another hundred is created. Therefore, the answer becomes 6 hundreds, 2 tens, and 7 ones (627).
- Noticing the pattern is important. The next step is to structure the pattern, that is, find out why it behaves the way it does. Challenge the students to use Place Value People (Copymaster 1) to model some examples of the 11 x pattern. Slides 8 and 9 of PowerPoint 2 illustrate 11 x 27. You might use the slides initially or allow students the opportunity to represent calculations themselves first. Essentially the pattern works because of the distributive property. Multiplication by eleven is the sum of multiplying by ten and one.
Symbolically this property can be written as 11 x 27 = (10 x 27) + (1 x 27) = 270 + 27. The vertical algorithm on Slide Nine better illustrates how the digits in the second factor contribute hundreds, tens and ones to the product. - What happens if the two digits in the second factor add to a number greater than nine?
- Students might recognise that if the sum of a + b > 9 (for any number 10a + b) there is more renaming required as tens are renamed to form hundreds. Slide Ten shows the calculation of 11 x 79 which is a good example.
- Challenge the students to practise their skills in calculating 11 x any 2-digit whole number. You might have a quiz to see how quickly they can use the digit pattern to find products. You might express the method as an algorithm (step by step procedure), such as:
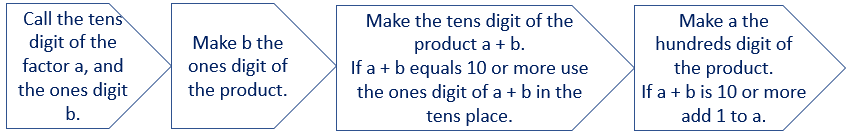
- If time permits, set related extension problems: The solutions are:
- Develop an algorithm for multiplying a three-digit whole number by 11.
- Develop an algorithm for multiplying a two-digit number by 101.
- Develop an algorithm for multiplying a two-digit whole number by 111.
The solutions are:
- For any three-digit number, 100a + 10b + c (written as abc e.g. 345) the product when it is multiplied by 11 is a thousands, a + b hundreds, b + c tens, and c ones.
For example, 345 x 11 = 3 795. Note that renaming is needed when a + b and/or b + c equal ten or more. - For any two digit number, 10a + b (written as ab e.g. 68) the product is 'a' thousands, 'b' hundreds, 'a' tens and 'b' ones. No renaming will be needed.
For example, 68 x 101 = 6 868. - For any two-digit number, 10a + b (written as ab e.g. 34) the product when it is multiplied by 111 is a thousands, a + b hundreds, a + b tens, and b ones. Note the renaming needed if a + b > 9. For example 35 x 111 = 3 885.
Session 3
In this session students investigate how many tens are in a whole number to four places.
- Remind students about their learning from Session Two.
What is the product of 10 x 26? How do you know?
What is the product of 10 x 49? How do you know?
What is the product of 100 x 83? How do you know? - If necessary, use Place Value People to model the 10 x calculations (ten sets of the other factor). Discuss why modelling 100 x 83 might not be efficient and that thinking about pattern is more helpful.
What is 83 composed (made up) of? (8 tens and 3 ones)
What is 100 x 3? Why is the product the same as 3 x 100? (Commutative property)
What is 100 x 8? So, what is the product of 100 x 80? Why? (Do students recognise the effect on the digits in the product of multiplying by ten?) - Ask students to model the number 245 with Place Value People (Copymaster 1).
You need to make teams of ten for sports day. How many teams of ten can you make with 245 people? - Ask students to anticipate the result of making tens then justify why they believe 24 tens exist in 245. Their explanations should include the fact that ten tens are nested in each hundred.
How might we record what we have found in an equation? - Let students offer possibilities like 24 × 10 = 250 or 240 ÷ 10 = 24. Discuss the meaning of the symbols, especially the division sign. In this case the process is measurement, i.e. How many tens make 240?
- Ask: What might we do with the extra five people?
Some students might suggest that five is half of ten or that there are 24.5 tens in 245. - Would you be able to make teams for games of Tapu Ae? Or ki-o-rahi teams (Tapu Ae has a minimum of 5 players aside and ki-a-rahi has 8 aside). Does knowing about the product of 10 help?
- Ask: How many tens can be made with …609 people? 444 people? 930 people? With that information can you easily find out how many teams of 5 could be made and about how many teams of 8. What is your reasoning behind your answer?
- Do the students justify their answers by referring to the tens nested within the hundreds? Make 1 000 with Place Value People by attaching ten one hundred sheets together with a single staple.
How many people are in this stack? (1000 since there are ten hundreds) - Make the number 1 728 using Place Value people. Work out how teams of ten people can be made with that number.
- Look to see that students correctly model 1 728 with one thousand stack, seven hundreds sheets, two ten strips and eight singles.
Do they unpack 100 tens in 100, 70 tens in 700, and 2 tens in 20?
Do they name and justify that there are 172 tens in 1 728 (or 172.8)? - Ask: How many teams of one hundred people could be made with 1 728 people?
- Look to see if your students recognise that ten hundreds exist in 1000, and another 7 hundreds exist in 700, making 17 hundreds altogether. If students give an answer of 17.28, recognise that this a very sophisticated answer since 0.28 means 28 hundredths. Record the operations of finding out how many tens and hundreds are in 1 728 as equations; 1720 ÷ 10 = 172 and 1700 ÷ 100 = 17.
What patterns do you see in dividing by ten and one hundred? - Provide your students with Copymaster 4 that contains a set of related problems to work from. Look for students to develop fluency with renaming whole numbers.
- Mark the Copymaster together and discuss the strategies students used to solve the problems.
Session 4
In this session students put the concept of nested place value to work by solving problems. Most of the problems involve addition and subtraction, but a multiplicative view of place value is essential to the development of fluent strategies. Consider framing these problems in contexts relevant to your students and local area (e.g. number of students at our school each year, number of visitors to the library).
- Introduce Slides 1 and 2 of PowerPoint 3. You could use a large set of Place Value People to model the operations of 63 + 8 = 71 and 630 + 80 = 71 or simply play the animations and discuss what happens. The key idea is that students recognise the connection in both operations, that is 630 + 80 is the addition of 63 + 8 in units of ten.
What is the sum of 6 300 and 800? How do you know? (63 + 8 = 71 in units of 100, so 7 100) - Give your students other examples to calculate, with or without the support of Place Value People, depending on their fluency. Good problems are:450 + 70 =
880 + 60 =
390 + 90 =
940 + 80 = - Slides Three and Four of PowerPoint 3 deal with the same principle applied to subtraction. The examples of 82 – 7 = 75 and 820 -70 = 750 illustrate how a subtraction result with ones can be used to work out a result with units of ten. The principle works with units of any equal size, e.g. 8200 – 700 = 7 500 (units of 100).
- Give your students other examples to calculate. Check to see that they can demonstrate what is occurring with the quantities in the calculations, using Place Value People. Good examples might be:
430 – 60 =
910 – 80 =
540 – 90 =
820 – 70 = - Provide your students with Copymaster 5 to work from in pairs. This worksheet consolidates and extends the concept of renaming a number to make calculations easier. Note that the principle is extended to four-digit whole numbers. Some students may need support, including modelling with Place Value People (Copymaster 1).
Session 5
- To consolidate the concept of nested place value, introduce and play the game Cover Cathy Crocodile 4 digits. The game can be made using Copymaster 6. Easier forms of the same game are available in the level two place value units (Cover Cathy Crocodile: 3 digits and Cover Cathy Crocodile: 2 digits)
- The purpose of the game is to develop students’ fluency in renaming whole numbers up to four digits. To assess students’ ability to rename pose this question:
Using thousands, hundreds, tens and ones, make up at least five names for 4768.
For example, the first name might be 4 thousands, 7 hundreds, 6 tens, and 8 ones. The second name might start with 47 hundreds…
Which name would be most useful to solve the problem 4768 + 900 = ?
Dear family and whānau,
This week we have been exploring place value with whole numbers. We looked at the number of tens and hundreds in numbers like 4762 and used that knowledge to solve addition and subtraction problems. To help us we used a model called Place Value People so we could see what happened to the numbers we worked with. Discuss this strategy with your child. They can share how they used it to solve addition and subtraction problems.