The purpose of this unit is to develop knowledge and understanding of the place value of two-digit numbers, and to support students in generalising and applying known single digit facts, and patterns associated with these, to two-digit numbers to 100.
- Describe representations of numbers to 100.
- Understand the meaning of ‘two-digit’ number.
- Make and record any two-digit number using equipment, symbols and words.
- Use knowledge of basic facts to ten to add and subtract decades to 100.
- Recall and apply groupings with numbers to 100.
- Partition (decompose and compose) two-digit numbers in different ways.
- Trade and exchange using a different marker for ten.
- Understand the terms face and place value.
- Use and explain place value houses.
This unit of work follows Teen numbers (building with ten) in which place value is introduced and the understanding of ten as 1 group of ten is established. In this unit, place value understanding is generalised to apply to all two-digit numbers.
As students work with a variety of place value materials, the connections between different representations should be clearly made and the key ideas developed. Understanding what is meant by a digit, and thus a two-digit number, allows the ways in which patterns are explored with numbers to ten to be generalised to larger two-digit numbers. This also develops understanding of the variety of ways in which numbers can be composed and decomposed, and develops understanding of the terms face and place value.
Students should have already had opportunities to compose tens from single units using equipment such as nursery or ice block sticks, or plastic beans and canisters. As they work with larger numbers, the convenience of pre-grouped materials becomes evident. However, students should continue to be given opportunities to compose and decompose, partitioning numbers in different ways. It is a considerable shift for children to then use materials in which the ten looks completely different from the ones (for example, money) and to trust the ten for one trade. The greatest abstraction of the digits in our number system is seen when the tens and ones look exactly the same and can only be differentiated by their place (which denotes their value).
This unit also introduces students to the semi-abstract construct of place value houses and are therefore introduced to the foundations for an understanding of larger numbers. The transition from making and seeing two-digit numbers with materials, to being able to imagine and describe them, to finally solving problems using number properties which depend on an intuitive place value understanding, is one that should be kept in mind as we scaffold student understanding in this unit.
Links to the Number Framework
Stages 4 – 5
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate the tasks include:
- adapting the number of activities used in each session in response to students' progress
- working with numbers to 30 before extending to numbers to 100
- using some of the suggested activities as independent activities for students ready for extension
- providing opportunities for students to work in pairs and small groups in order to encourage peer learning, scaffolding, extension, and the sharing and questioning of ideas
- working alongside individual students (or groups of students) who require further support with specific area of knowledge or activities
- creating a class chart of key knowledge, representations, and ideas for students (and the teacher) to refer back to during each session
- extending students by providing word problems, reflecting a current and relevant context, that require students to apply the skills developed throughout the unit
- applying gradual release of responsibility to scaffold students towards working independently
Using the place value language structure within te reo Māori to develop and reinforce a conceptual understanding of place value. This was first introduced with teen numbers and continues to numbers greater than twenty. For example:
- Rua tekau mā tahi (two tens and one, 21)
- Rima tekau mā toru (five tens and three, 53)
In addition to supporting a conceptual understanding of the place value of numbers, the use of te reo supports the identity and language of Māori students. Other relevant kupu that could be included in this unit and used throughout other mathematical learning might include tatau (count), uara tū (place value), mati (digit), uara mati (face value), and moni (money).
- MAB base ten 1 cm cubes and tens
- Place value houses
- Place value equipment: nursery/ice block sticks, hair ties, beans, containers, abacus, arrow cards
- Copymaster 1, Copymaster 2, Copymaster 3, Copymaster 4, Copymaster 5
- Access to e-ako maths or the Number Facts Games collection: Number pairs: Decades to make 100, Hundreds frame: Decades that add to 100
- Dice
- Playing cards
- Play money
- Resources to create a class chart
Select one or more activities from the several activities that are suggested for each session in this unit. Alternatively, the activities suggested for each session could span multiple sessions. Many of the activities could also form the basis of independent practice tasks or follow-up task stations in response to whole class teaching. Ensure that you roam and provide support to small groups of students, or to individuals, in response to their demonstrated needs.
Session 1
SLOs:
- Describe representations of numbers to 100.
- Understand the meaning of ‘two-digit’ number.
- Make and record any two-digit number using equipment, symbols and words.
Activity 1
- Begin by showing a Slavonic abacus to the students. Ask them to share all they know or notice about it. (for example: there are 10 rows, there are 100 beads altogether, ten beads make up each row, in each row there are two colours and each of these colours is 5 beads, there are twenty lots or groups on 5 in 100). Record the ideas generated on a chart.
- Ask the students to explain to a partner how they would go about counting all the beads and have a student demonstrate their strategies while their classmates/group members count with them, using the demonstrated strategy (one by one, in fives, ten at a time, fifty + fifty...).
- As a class, practise counting in tens: ten, twenty, thirty, forty... stress the last syllable, ‘ty’. Record on the chart the symbols and words for the decade numbers: 10, 20, 30...). Highlight the ‘ty’ ending and note the difference from ‘teen’ numbers.
- Display the abacus and a hundreds board, making the connection between the two pieces of equipment. Model a number on the abacus and identify the number on the hundreds board. Students need to see how these pieces of equipment complement each other.
NB. When modelling, for example 34, on the abacus, first move all the beads to the right hand side of the abacus. Then slide 3 lines of beads and 4 single beads (31, 32, 33, 34) across so that their position matches the position of those numbers on the hundreds board. (If all the beads begin on the other side, when you slide the 4 beads across they will incorrectly match the position of 37, 38, 39 40 on the hundreds board.)
- Hide the abacus, slide the beads to make a number, for example 47 and have the students in pairs describe the number made with beads. For example: a student might describe 48 as “there are four full rows of ten, that’s four tens, a group of five and three more beads which makes 8. There are two beads left that aren’t moved across.”
Record students' descriptions on the chart. Uncover the abacus and confirm. Repeat this a number of times to elicit and record the tens and ones language.
Activity 2
Record the word ‘digit’. Ask the students, “ What does this word mean? (it is a numeral symbol which represents a number). Tell the students that ‘digits’ is also another word for the name fingers and that "digit" comes from the fact that the 10 digits on their hands correspond to the 10 numeral symbols that we use in our number system. Record some two-digit numbers suggested by the students. Ask if 20, 10, 7, 100 are all two-digit numbers. Discuss (NB: 100 is a three digit number).
Activity 3
- Provide students with a variety of place value equipment: nursery/ice block sticks, hair ties, beans, containers, abacus, arrow cards. You might just introduce one to start with and then gradually the types of different equipment available to students. Have them sit facing a partner, with a book placed in the middle to act as a barrier. Each partner should not see their partner's equipment.









- Have the students play Digit Displays (purpose: to make and describe representations of two-digit numbers). One student makes and describes any two-digit number using the place value equipment and hides this from their partner who must represent the number using arrow cards. They disclose and compare the results. If the partner is correct they ‘keep’ the digit cards, and roles are reversed. Each student has three turns and tries to collect all three arrow card sets. Ensure you model how to play this game for students before letting them work in their pairs.
Activity 4
- Play Place Value Loopy (Copymaster 2) to consolidate understanding of tens and ones in numbers to one hundred. Cut the loopy sheets into individual cards and distribute these to students evenly. The student with the start card reads the first clue. The student with the answer to that clue reads the number answer aloud, then reads their clue. This pattern of question and response continues until the final card is read.
It is useful to have a practice game then to redistribute the cards and time the class/group performance. Each subsequent time the game is played, the aim is for the group to better the previous time set.
Session 2
SLOs:
- Make and record any two-digit number using equipment, symbols, pictures and words.
- Use knowledge of basic facts to ten to add and subtract decades to 100.
Activity 1
- Begin the lesson by writing ‘Pattern hunt’ on the class chart. Tell the students they are going to use what they already know to make working with all two-digit numbers easy.
- Have students work in pairs. Each pair should have chart paper, pens and place value equipment (an abacus or beans and containers). Set a short time limit (eg. using an egg timer, length of a tune, 3 minutes).
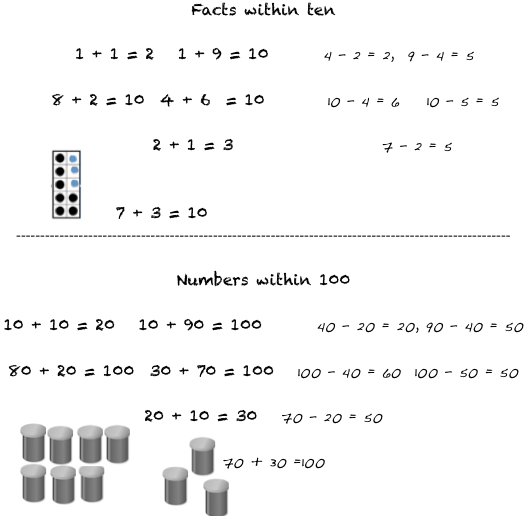
- Have students must fold their chart paper in half. In the top portion they write Facts within 10 and must record all facts they know within and to ten. (Both can record at the same time). In the lower portion they write Numbers within 100 and show, using pictures, words, symbols and equations, the ways in which their facts within ten help them work with two-digit numbers.
- Have students share their posters and model their ideas on an abacus for the class to see.
Activity 2
- Circulate a tray with place value equipment (e.g. beans and full tens containers, nursery stick bundles of ten and units) and some story problems. As the tray is passed round from student to student, each person should draw out a problem, read it to the class, model it with equipment, before passing the tray to the next person. Students could do this in pairs, if necessary. Copymaster 1 contains story problems. You could adapt these to reflect contexts that are more relevant, engaging and meaningful to your students. Consider how links to cultural knowledge and learning from other curriculum areas could be made through the adaptation of these problems.
- Conclude the lesson by describing (without materials) two-digit numbers. Have the students imagine these as they are described and record the number (on paper or with their finger in the air). For example: The teacher says, “Five rows full rows of beads on the abacus and seven single beads, 5 of one colour and two of the other.” Students write 57.
Session 3
SLOs
- recall and apply groupings with numbers to 100
- partition (decompose and compose) two-digit numbers in different ways
Activity 1
- Begin the lesson by circulating the abacus and asking each student to model and say complementary pairs of decades to 100. For example: A student slides across thirty beads and says, “Thirty plus seventy is one hundred.”
- The teacher repeats this, hiding the abacus, and saying how many beads are moved (decades). Students write the complementary decade number.
- The teacher now models a number that is not on the decade, for example 28, and the students are asked to describe to a partner what is left. “Two (to make thirty) and seventy. So its seventy two.” Emphasise the composing of the ten with the two single digits and the number of whole decades that remain. Highlight the connection to basic facts.
- Repeat 2 (above) this time with complementary numbers that are off the decade: eg. 66 and 34, 75 and 25, 17 and 83. Have the students picture these in their heads, record their answer and check with the beads as the abacus is revealed.
Activity 2
Enlarge and display a “Matching Pairs to 100” sheet (Copymaster 3) and have the students, either as individuals or in pairs, find and record these as quickly as possible. Have the abacus available for reference.
Activity 3
Work with students on games that encourage students to know the pairings of decades to 100. These games are available within e-ako maths or from the Number Facts Games collection:
Activity 4
- Have students play First to Forty. Students need to have beans and containers, a set of playing cards 1-9, a dice with + or – symbols marked on each of the six faces.
- Each student writes 25 and makes it using place value equipment. Players take turns to roll the dice and turn over a playing card. They need to either add or subtract the number shown on their playing card from their materials, and write the relevant equation. You could also adapt this to have each students play in partners, with each student telling their partner whether to add or subtract on each turn. The winner is the first student who makes at least forty.
For example: if a student rolls + and turns up an 8 they make 33 with the equipment. They record 25 + 8 = 33.
Activity 5
- As a group, discuss the language “compose” and “decompose”. Make connections to real life examples (e.g. we compose music or writing, waste material decomposes or breaks down). Model and record on a chart other names for two-digit numbers to 100. For example: 33 is the same as 3 tens and 3 ones and also 2 tens and 13 ones 45 is the same as 4 tens and 5 ones and also 3 tens and 15 ones. Provide materials for students to fold back to and use, as necessary.
- Ask students to think of their own example and share them with a partner. Ask several students to share and demonstrate their two-digit numbers with place value materials.
Session 4
SLOs
- recall and apply groupings with numbers to 100
- trade and exchange using a different marker for ten.
- Introduce MAB equipment (MAB stands for Multi-base Arithmetic Blocks, also called Place Value Blocks). Ask the students what is the same and different about this material compared with equipment used so far (same, tens and single units or ones; different you can’t break up the tens as you need to exchange them for ten ones).
- Have students work in pairs to play First to Forty as in Session 3, first explaining that they will still be composing and decomposing numbers, however the process will be one of exchange, ones for ten and ten for ones.
- Introduce play money with $1 coins and $10 notes. Ask the students to comment about the material as in 1. above. Highlight that money is like other place value material we have used, but the ten looks very different from the ones. We can’t see a similarity between the coins and the $10, yet ten $1 coins have the same value as one $10 note. Point out that when we go shopping we operate and trading or exchange system which depends on the value of things we buy and what change we might receive.
- Have students play Banker’s Bonus. Provide students, in small groups, with $1 coins and $10 notes and a set of Banker’s Bonus instruction cards (Copymaster 4).
- Have students choose a starter card from the Banker’s Bonus pile and take that amount of money. They then take turns taking reading and following a Transaction instruction card, composing and decomposing their amount of money accordingly. Other players check for accuracy. The winner is the player who reaches $100 first. They are awarded a $10 bonus with which to begin the next game.
Session 5
SLOs
- understand the terms face and place value
- use and explain place value houses
Activity 1
- Display a place value house and asks the students what they notice about it (e.g. it has three ‘rooms’, the rooms are called Hundreds, Tens and Ones, it is called the Trend Setter House because there are more houses like this one, so this one ‘sets a trend’ or ‘shows what the others will be like’).
- Ask what we might call this house. Accept students ideas, then tell them we call it a place value house. Ask them to suggest why it has that name. Say, "let’s find out.”
- Have the students work in pairs. Distribute to each pair a place value house, MAB blocks, a whiteboard marker and pencil and paper.
- Have the students make one number between ten and ninety nine using the equipment provided and locate this in the appropriate place on the place value house. Ask the students to explain what they notice (i.e. the tens and ones have their own place).
- Have the students slide the blocks off the place value house till they are positioned below it. Using the whiteboard pen, have the students write the number in the PV house. Once again, ask what they notice (i.e. the number they write represents tens and ones).
Activity 2
- On a chart write the words ‘place value’ and ‘face value’. Have students in pairs write down what they think these terms mean. Share ideas. Look at each of the words: place (location or position), face (appearance or what we see) and value (worth). Writes a two-digit number on her PV house and circles the tens digit. Discuss its face and place value. For example: "95, the digits are nine and five. These are their face value or what they appear to be. Because of its place in the tens the nine’s place value is nine tens or ninety and the 5 is worth just five, which is both its place and face value."
- Have the students circle a digit on their whiteboard and discuss its place and face value.
- Conclude the activity by displaying the place value trendsetter house and asking students to describe the hundreds place value equipment (ten of the tens joined together). Show this block to the students.
Activity 3
- Have the students play in pairs What’s it worth?
Provide students with a scrambled set of the cards (Copymaster 5). They must work together to find the matching pairs in which the place value statement is true. Challenge students to create their own game to which there is one solution to use all their cards.
Dear family and whānau,
This week we have been learning about two-digit numbers focusing on the meaning of the tens and ones.
At home, please draw your child's attention to the numbers around you. For example, on the walk or drive to school, you might ask them to look for two-digit numbers (e.g. on signs and the dashboard) and tell you how many tens are in each number. You could also ask them to add tens to their number.
For example: "Look there's 24. What would it be if you added 30 more? What about if you took away 10?"
