The purpose of this unit is to develop students' knowledge and understanding of place value in three digit numbers. In turn, students are able to generalise from known two-digit facts, apply patterns associated with these to three digit numbers to 999, and are introduced to the concept of 1000.
- Consolidate place value understanding of 2-digit numbers.
- Develop understanding of 3-digit numbers by composing and decomposing numbers to 1000.
- Represent the structure of 2- and 3-digit numbers by modelling them with a range of materials.
- Develop understanding of simple benchmark numbers to 1000.
- Explore the structure and size of 1000.
- Use materials to explore powers of numbers and the difference between place and face value in numbers to 1000.
This unit of work follows the Level 1 unit Building with tens in which the place value structure of 2-digit numbers is explored. Within this, students developed their understanding of a group of ten objects as a unit and have begun to connect this idea to our numeration system. This developing place value understanding is generalised in this unit to apply to all three-digit numbers and to 1000.
As students develop key ideas with a variety of place value materials, the connections between different representations should be clearly made. Students begin by using materials to compose and decompose single units in tens (eg. beans and containers) and move to using pre-grouped materials. Materials become increasingly abstract to the point where non-proportional models are used. The representation of a quantity by digits alone is the most abstract. Here, the ability to competently use the same marker (digit) to represent different values, depends on the student having a sound conceptual understanding of the structure and patterns within our base ten system.
One focus of this unit is on building the understanding of the ‘trend setting’ structure of hundreds, tens and ones. This grouping of hundreds, tens and ones is repeated in our numeration system, as the size of numbers increases or decreases. It is a fundamental building block and must be well understood if students are to work intuitively with big numbers and decimals. An introduction to the magnitude of growth or ‘powers of ten’ is essential. As students begin to understand the multiplicative nature of our number system, they benefit from seeing what ten times bigger looks like with each place shift to the left.
‘Knowing’ numbers and being able to quickly partition them in a variety of ways enables students to develop efficient strategies for problem solving. It is therefore important that students have opportunities to compose and decompose three digit numbers in a variety of ways, as these making and breaking experiences build deeper knowledge of the place value structure. Knowing numbers also involves the students developing some personal ‘benchmarks’ of size. Having a sense of the relative size of 200, 250, 500, 750, 800, for example, provides the student with useful reference points for problem solving.
Maths language and communication skills continue to develop as students read, write and show three digit numbers, and talk about what they are doing. For example, using ‘ones’ or ‘units’ each time a number is described can be unnatural or awkward. Developing an implicit understanding that the 7 in ‘two hundreds, 3 tens and 7’ is 7 ones is useful. In these lessons mathematics communication is developed as students explain the link between place value materials and the meaning constructed from their use of them.
Links to the Number Framework
Stages 5- 6
The learning opportunities in this unit can be differentiated by providing or removing support to students, and by varying the task requirements. Ways to differentiate the tasks include:
- introducing fewer activities in each session
- working with numbers to 150 before extending to numbers to 1000
- providing extended opportunities for independent and guided practise of tasks
- providing opportunities for students to work in a range of small group, paired, and whole class settings, and as individuals
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific area of knowledge or activities.
Using the place value language structure within te reo Māori develops and reinforces a conceptual understanding of place value. This can be introduced with teen numbers, numbers to 100, and can continue with numbers greater than 100. For example:
- Kotahi rau, toru tekau mā rua (one hundred, three tens and two, 132)
- Iwa rau, iwa tekau mā iwa (nine hundreds, nine tens and nine, 999)
In addition to supporting a conceptual understanding of the place value of numbers, the use of te reo supports the identity and language of Māori students. You could also encourage students, who speak a language other than English at home, to share the words related to place value that they use at home.
- Abacus
- Plastic beans
- Plastic containers
- Ice cream containers
- Calculators
- Playing cards (enough for half a pack of playing cards per pair of students)
- MAB (Multibase Arithmetic Blocks) 1, 10, 100, 1000, also known as Dienes blocks
- Place value houses (Trendsetter and Thousands) (Material Master 4-11)
- Hundreds board (Material Master 4-4)
- Thousands Book (Material Master 4-7)
- Arrow cards (Material Master 4-14)
- Copymaster 1, Copymaster 2, Copymaster 3, Copymaster 4, Copymaster 5, Copymaster 6, Copymaster 7, Copymaster 8
- Access to the following digital learning object: Modeling numbers: 3-digit numbers
- 1 cent coin, a $1 coin, and a $10 (or pictures)
Select one or more activities from the several activities that are suggested for each session in this unit. Alternatively the activities suggested for each session could span across multiple sessions. You could also introduce these activities as independent practise tasks or stations for students to visit. Ensure you model and provide sufficient direct, explicit teaching around the tasks to enable students' effective participation.
Session 1
SLOs:
- Consolidate place value understanding of 2-digit numbers.
- Represent the structure of 2- and 3-digit numbers by modelling them with a range of materials.
- Explore the structure and size of 1000.
Activity 1: Skip Counting with Abacuses
- Begin the lesson by having students skip count to 100 in tens, fives, fifties and twenties. Have students take turns modelling this on the abacus, moving the relevant groupings of beads as the class counts (e.g. two full rows of beads are moved at each count as the class counts 20, 40, 60, and so on).
- Using the abacus, have a student make and describe a 2-digit number, screening this from the view of their classmates. For example, “there are seven rows of ten and 3 single beads”. Have the student choose a classmate to identify the number (73), then reveals it to the class. That student has a turn, repeating the task. Reverse the task by having the student who is modelling say which number they have made (40) and have a classmate describe what it looks like. (“Four rows of ten beads and no single beads.”) Each time the response is confirmed by revealing the abacus model. This could also be done in pairs using a digital abacus model.
Activity 2: Place Value Loopy
- Play Place Value Loopy (Copymaster 1). Distribute the cards to the class (or the group). In preparation for the game, first have the students read the lower clue on their card, eg. 'I have 2 tens and 0 ones. Who am I?’ on their card and name (perhaps with a partner) the number it describes (i.e. 20). Then have them think of what the clue for the 2-digit number that appears at the top of their card might be. This is the clue they will listen for and respond to as the game proceeds. You could have them use popsicle blocks, blocks, or drawn diagrams to represent the number as groups of tens and ones. The student with the START card begins the game.
For a greater challenge, time the game and have the students work together to improve their timed score.
Activity 3: Mr Bean
- Introduce the beans and containers place value materials to the students. If they have not already worked with these grouping materials, have the students make tens by filling containers with ten beans. Establish that one container represents ('is') a ten.
- Place a set of beans and twelve tens (in containers) in front of the class. Have students work with a buddy and have them take turns to describe what a 2-digit number would look like if they were to model it using the equipment. Their partner should state the number. For example, 71 is 7 tens and 1 bean.
- Write several 3-digit numbers in the range 100 – 150 on a chart and have the students take turns to describe these to each other as if they were modelling it with the equipment. For example, write 127. Students should describe this as “twelve tens and 7 (ones).” If necessary the students can skip count to check whether they are correct.
- Ask the students if a number (e.g. twelve tens) could be shown in any other way. Guide the conversation to the convenience of grouping ten tens as 100. You might demonstrate this by placing ten containers of beans in the ice cream container and securing on the lid. Agree that this container is one hundred.
- Repeat step 3 above with numbers 100 - 150, having the students name the hundred, tens and ones. For example, 148: 1 hundred, 4 tens and 8
- Write the words one, ten, hundred, group on chart. Show the children one bean. Name it Mr Bean.
Talk about how Mr Bean gets together with lots of other beans and how they organise themselves to have a party/ to go on a journey/ to have a sporting competition etc. Have the students return to their places and write a 3-digit number between 100 – 150 on their paper (eg. 137).
Have students write and illustrate a creative story, eg. The Adventure of Mr Bean and his 136 friends. Encourage them to use the vocabulary listed on the chart in their stories. Have the student share their stories with a partner. Display the stories.
Activity 4: Make and Take
- Show the students the MAB (Multibase Arithmetic Blocks).
- Have the students discuss what is similar about these, the beans, and containers. It is important to have them articulate that ten ones are ‘joined together’ to make a unit of ten, and ten of these are joined to make unit of 100.
- Have students play Make and Take in pairs.
Organise students into pairs. Distribute 15 tens and 1 hundred (represented using MAB), a dice and recording materials. Have students make one group of 70 with their equipment and both use this for the game. Explain and model the game as described below:
- Each student has a different target which they aim to be the first to reach: Player One must make 150 by adding tens and Player Two must make 0 by subtracting tens.
- Players take turns to roll the dice, model the number made and record the equation as they do so. For example: Player One, whose target is to make 150 by adding tens, rolls 4 and adds 4 tens to 70, making 110. He models this with materials, in the process exchanging 10 tens for 100. He records 70 + 40 = 110. Then Player Two, whose target is to make 0 by subtracting tens, rolls 5. She exchanges 1 hundred and 1 ten for 11 tens from which she subtracts 5, leaving 6 tens. She records 110 – 50 = 60.
- The game continues until one player has made (or exceeded) their target.
- For extension, students could adapt the number targets and operations used in the game.
Activity 5: Dots
- Show the students an image of dots in a random grouping. (Copymaster 2). Have the students say how many dots they think there are. Ask them to justify their estimate. Tell them the total (123).
- In pairs or small groups ask students to come up with ways to count the dots. Share approaches. Confirm or suggest the idea of grouping in tens.
- Give each group a copy of the dot image, and ask them to find out how many dots there are by circling into groups of 10. Ask them to share how many tens (13) and how many left (3), giving a total of 133.
- Show the students a dot image of 100 (Copymaster 2). Have the students say how many dots they think there are. Ask them to explain their thinking and make links to the ten groups of ten structure of the equipment they have been working with.
- Conclude the lesson by recording what has been learned, highlighting grouping of ten and ten times ten. Emphasise that 10 is ten times bigger than 1 and that 100 is ten times bigger than 10 and one hundred times bigger than 1.
Session 2
SLO:
Represent the structure of 2- and 3-digit numbers by modelling them with a range of materials.
Activity 1: 3 Digit Decades
- Have the students work in pairs. Give each pair MAB hundreds and tens equipment. Write a decade number between 120 and 250 on a chart .
- Skip count together in tens to that number. As you do so have one student in each pair lay down a ‘ten’ (MAB ) for each count. Have the other student in the pair check how many tens there are at the end of the count. For example, the students skip count in tens to 230. They find this is 23 tens. Record 230 = 23 tens on the chart.
- Repeat in te reo Māori, noting how the structure of the words helps us to understand the number. Rua tekau (20, 2 tens); toru tekau (30, 3 tens);…rua rau (200, 2 hundreds); rua rau, tekau (210, 2 hundreds, ten); rua rau, rua tekau (220, 2 hundreds, 2 tens); rua rau, toru tekau (230, 2 hundreds, 3 tens)
- Have the students twice exchange ten 10s for one 100 and model 230 with hundreds and tens.
- Add to the recording on the chart: 230 = 23 tens = 2 hundreds and 3 tens
- Repeat several times with different decade numbers, 120 – 250.
Activity 2: Measuring Heights
- Explain to the students that the class is going to investigate the range of heights of the students in the class.
- Using MAB ones cubes, set the task for the students to each measure how long their pencils are in cubes, rounding to the nearest cube. Have them line up the cubes alongside their ruler, confirm the length in centimetres, and then exchange ten single cubes for one ten block as appropriate. Place the ten(s) and ones along the ruler once again for further confirmation.
- Explain that the MAB equipment (ones and tens only) is now going to be used to measure how tall the teacher is because she needs to know this (e.g. for her passport application). Lie down and have students place a marker at your head and feet. Stand up and see where students placed the markers.
- Direct one student to measure the distance between the markers by carefully laying tens blocks, end on end, while the other students count the number of blocks. Use ones blocks to complete the measure. You might also discuss why using tens is a better idea than using all ones for this task (e.g. more efficient, easier to count and move). Describe the number using the developed terminology: e.g. 17 tens and 4 ones. Students are asked to discuss with a partner if there is another way to say this.
- Introduce a 1 metre ruler. Compare it to the MAB: a single cube = 1cm, a ten rod = 10cm, ten 10cm rods = 100cm or 1 metre. Confirm the height of the teacher using the ruler (e.g. the teacher is 1 metre/m and 74 centimetres/cm or 174 centimetres/cm).
- Emphasise the connection between the one hundred MAB flat and a 1 metre ruler. Each is ten groups of/times 10.
- Have the students work in pairs to measure each other using 10 centimetre MAB rods, converting their measurements into metres and centimetres.
Activity 3: Paperclips
- Have the students work in groups of four. Give each group 100 – 200 paperclips. Pose the challenge. Another group needs to see at a quick glance how many paperclips you have. You have 5 minutes to make a display with your paperclips that another group can ‘read’ at a glance.
- Have the students visit the displays made by other groups. If they think the number of paperclips is immediately evident, each visiting student awards that group one coloured counter.
- The groups return to their own display to see how others have voted.
- Discuss what the students did, highlighting the grouping decisions made by each group. Comment on those who used a tens and ones structure.
Activity 4: Using Words and Symbols
- Conclude the lesson by writing several numbers 100 - 250 on the class chart.
- Beside each, write other ways of recording these using words and symbols.
For example, 182- 1 hundred, eight tens and 2 (ones)
- 18 tens and 2 (ones)
- one hundred and eighty two (ones)
- Kotahi rau, waru tekau mā rua.
- Record student contributions as they describe what they have learned.
Session 3
SLOs:
- Develop understanding of 3-digit numbers by composing and decomposing numbers to 1000.
- Develop understanding of simple benchmark numbers to 1000.
Activity 1: Compatible Numbers
- Record 200 on the class chart. Ask the students what they know about 200 and record the students’ ideas.
- Write ‘compatible numbers’ on the class chart. Discuss the meaning of compatible numbers and model examples. Explain to students that they are going to work in pairs to investigate compatible pairs to 200. Each pair has access to MAB and half a pack of playing cards, excluding face cards (2 sets of cards 1-9).
- Have students take turns turning over two cards to make a 2-digit number, recording this, and then modelling the number with MAB. Their partner must then make the compatible number to 200. The first student then checks that the two models do indeed combine to make 200 and records the complete equation.
- For example, Student One turns over playing cards 8 and 3, models 8 tens and 3 ones, and records 83. His partner models 7 ones, 1 ten and 1 hundred and says one hundred and seventeen. Student One adds the two models together, exchanging ones for a ten and tens for a hundred. Once confirmed that they do indeed make 200, the student completes their written equation: 83 + 117 = 200. Student Two repeats the task. They continue till they have at least four correct equations which show complementary numbers to 200.
- Use the class chart to record some of the compatible number equations for 200 generated by students.
Activity 2:
- Model the hundreds board task from p14 of Book 4, Teaching Number Knowledge, using the page showing 101 – 200 in the Thousand Book (Copymaster 3).
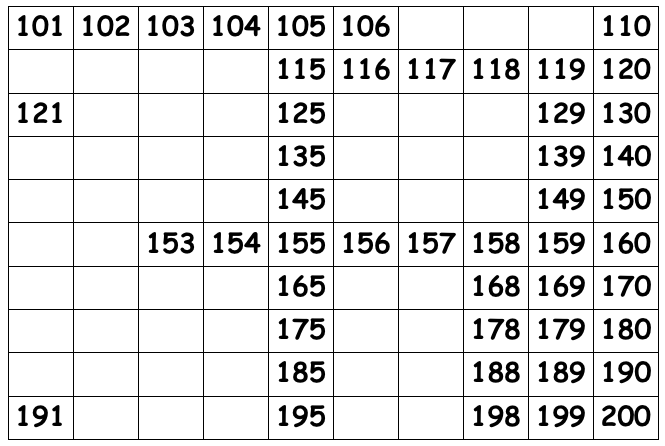
- Explore these symbols.
← left: subtract 1, -1
→ right: add 1, +1
↑ up: subtract 10, -10
↓ down: add 10, +10
- Model at least two examples using materials. For example: 125 ← ← ↑ ↑. Model 125 with MAB materials. Remove 2 single cubes (-1 twice), remove two tens (-10 twice) leaving a model of 103. Record the equation that explains what was done: 125 – 22 = 103
- Pose a problem using both the addition and subtraction arrow symbols. Make the thousands book page/s and MAB available to students. Have them share their result. Record an appropriate equation. This may involve several steps.
For example 161 ← ↓ ↓ → → : 161 – 1 + 160, 160 + 20 = 180, 180 + 3 = 183.
- Have students work in pairs to pose a problem for their partner by writing a number and code using symbols. Explain that their problems should be in the range 100 – 300.
- Have the students pair share some of their equations. Ask them to talk about their use (or not) of place value materials.
Activity 3: 3-digit Loopy
- Explain to the students that they are going to create their own class set of the game, 3-digit Loopy, using numbers up to, and including, 500. Remind them of the Place value Loopy game (in Session 1), in which one clue leads to the next. Show an example of a game card.
- Display Copymaster 4 on a chart. Beside each line, record the name of a student. Make it very clear that the top number is the answer to another person’s clue. Explain that the clue that they write does not relate to the top number and that the role of the first and last student to write ‘Start’ and ‘End’ respectively.
Check to see if the students have questions.
- Distribute blank cards to the students and have them create their card, on which they give two clues for their given number, as in the example.
- Have partners check each other’s clues and tick the list when they have verified that the clue does in fact match the given number.
- Collect the cards and redistribute them. Play 3-digit Loopy. Reflect on the game’s success.
Session 4
SLO:
- Explore and understand the structure and size of 1000.
Activity 1: 3-digit Loopy
- Play the 3-digit Loopy class game created in Session 3.
Activity 2: Counting to 500
- As a class/group count to 500 in tens. Have two students model this simultaneously using MAB equipment. They will make ten for one exchanges of equipment, as centuries are reached.
- Count to 500 in hundreds.
- Count back from 500 modelling the exchanges in reverse.
Activity 3
- Write ‘one thousand’ in words on the class chart. Ask the students to share all they know about one thousand. Record their ideas on the chart. If the students don’t suggest it independently, make the link to the counting exercise in the activity 2 by combining 500 + 500, highlighting : 5 + 5 = 10, 50 + 50 = 100, 500 + 500 = 1000.
- Conclude by asking, “ What does 1000 look like?” Students may suggest ten one hundreds. If so have a student model with ten one hundreds.
Activity 4: 1000 Dots
- Show the dot images from the random dot activity in Session 1 (Copymaster 2). Ask the students to explain to a partner what 1000 dots will look like. Record their ideas.
- Show the first images (882) dots on Copymaster 5. Ask, “Is this 1000 dots? Who thinks yes? Who thinks no? Why?” Discuss.
Show the second image (1000) dots and ask the same questions. Highlight the powers of 10: 1 dot, ten times bigger is 10 dots, and ten times bigger is 100 dots and ten times bigger is 1000 dots.
Activity 5: Coin Exploration
- Show the MAB 1000 cube. Place beside it a single cube (1). Have pairs of students record in both words and numbers their ideas about what they see. Together explore the Modeling numbers: 3-digit numbers learning object.
- Add a metre ruler to the 1000 cube and the single cube and have the students add to their record of ideas. (Rove and check that they do understand that 1000 cubes is 10 metres and why.)
- Add a 1 cent coin, (or picture of 1 cent coin, Copymaster 6), a $1 coin, and a $10 note to the collection and have the students add to their record of ideas. Circulate and check that they do understand that 1000 cents is $10 and why. You might use this as an opportunity to explore the history of coins in New Zealand and other countries that are relevant to your students (by 1989 the issue of 1 and 2 cent coins had stopped. Both were demonetised in 1990).
- Distribute poster paper to each pair. Pose the challenge: ‘Using words, numbers and pictures, make a poster for our maths wall showing visitors to our room all that you know about one thousand. Explain on your poster why our number system is known as a Base Ten system'. Share completed posters as appropriate.
Activity 6: Code Game
- Play “Code Game” by having students make coded clues for their classmates to solve. Make MAB (ones, tens and hundreds) available to students. Distribute Thousands Books and open arrows (+ and – 100) to pairs of students. Have students select a starting number from 100, 200, 250, 500 or 750 and create and solve each other’s arrow codes.
- Discuss the challenges associated with adding and subtracting ones, tens and hundreds. Ask students to explain whether/how the Thousands Book or MAB equipment was used.
Session 5
SLOs:
Use materials to explore powers of numbers and the difference between place and face value in numbers to 1000.
Activity 1: Place Value Houses
- Make MAB available to the students. Have students work in pairs, sharing a Trendsetter Place Value House and a whiteboard marker.
- Have students take turns to write and model a 3-digit number. For example Student one writes 345 in the place value house and student two models this using MAB.
- Highlight and review the name “Trendsetter house” and the hundreds, tens and ones headings. Have the students suggest what the next house might look like. Have them draw and explain their ideas on the class chart.
- Introduce the Thousands House and discuss the repeating hundreds, tens and ones headings. Repeat step 2. above, this time with a number between 1000 – 1999.
Activity 2: Fish for 1000
- Have the students play Fish for 1000 (Copymaster 7), making MAB available. The game can be played by up to four players and the winner is the person with the most pairs of cards (one word card and one numeral card) that represent 1000. Players may have numerous pairs that correctly show other values, but it is the pairs of 1000 cards that decide the winner. Model the following process for students before allowing them to play the game:
- shuffle the cards and have students take 5 cards each. Remaining cards are placed in the centre face down.
- each player finds the word cards that match the numeral cards in their own hand. They place matching pairs in front of them once another player has verified that the pair does match. For example, Player one has the numeral card '374' and a word card describing this number , ‘I am 37 tens and 4 ones’ in their hand. These make a matching pair. They show this pair to another player, who verifies the matching pair. Player one places their matching card pair in front of themselves. Clues can be verified using place value materials.
- If a player has a numeral card and they want a matching card they must give a word clue that describes the numeral card. The word clue may or may not be the precise matching clue that another player holds. If a player has a word clue card he must interpret this and ask for the appropriate numeral card from another player.
- Players take turns to ask, “Have you (naming a particular player) got …..?”If the player who is asked does not have that card, the questioner is told, “Go Fish” and they take a card from the pile in the centre.
- The game proceeds till all cards have been used and matching pairs are displayed in front of the players.
Activity 3: Arrow Cards
- Write a number between 1000 and 1999 on a set of place value houses, for example, 1503. Write ‘face value’ in the class chart and record the face value for each digit. Ask students to explain the ‘place value’ of each of the digits. Have the students explain the different between face and place value and record their explanation/s.
- Distribute arrow cards to pairs of students. Have them make a number between 1000 and 1999. For example:
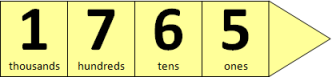
- Introduce the game, Zap (Book 4 Teaching Number Knowledge, p26). Ask the students to ‘Zap’ (remove) the digit in the tens place from their number and identify how much has been removed. Have them read their new number, emphasising the correct way to read a number that has zero as a place-holder. (for example: one thousand, seven hundred and five; or seventeen hundred and five). Have students repeat this activity several times before using calculators to play Zap.
Activity 4: Thousands and Trendsetter houses (extension)
- Display the thousands and trendsetter houses. Invite a student to write a number of their choice, composed of up to six digits, on the houses. Have the student ask a classmate to read the number and to say an interesting fact about the recorded number. For example:
- A student writes 50 000. The classmate reads ‘fifty thousand’ and says, ‘If it had another zero it would say five hundred thousand and it would be ten times bigger.’
- A student writes 543 210. The classmate reads ‘five hundred and forty three thousand, two hundred and ten’ and says ‘if you took away three thousand it would say five hundred and forty thousand, two hundred and ten.’
Activity 5: 11,111 (extension)
- Teach the students the game 11,111 (Copymaster 8). Allow them to play it in pairs or small groups.
Dear families and whānau,
In class we have been learning about place value in numbers to 1000. Help your child play the Licence Plates game at home.
This activity will help your child:
- read 3-digit numbers (and the occasional 4-digit number for cars registered before April 2001)
- recognise the place value of each digit in a 3-digit number
What to do:
- Take a walk or park somewhere where you can se a road. Work with your child to read the numbers on vehicles' license plates. As you read each number together:
- Ask your child questions about the numbers you see: What number is in the ones place? The tens place? The hundreds place? The thousands place?
For example in the number 723, the 3 is in the ones place, the 2 is in the tens place, the 7 is in the hundreds place. - Challenge your child to reorder the digits to make the largest number possible.
- Challenge your child to reorder the digits to make the smallest number possible.
- Challenge your child to reorder the digits to be as close as possible to a preset target number.
You may also enjoy making numbers together in the Modeling numbers: 3-digit numbers learning object.
Thank you for supporting your child in consolidating this important place value understanding.