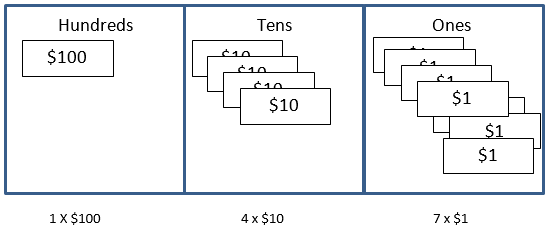
This unit supports students learning to understand the structure of two-digit numbers and how to operate with them.
Session One
- Calculate the gains and losses in a game of Snakes and Ladders.
Session Two
- Represent two digit numbers with play money.
- Add and subtract two digit numbers.
Session Three
- Use ‘up through ten’ and ‘back through ten strategies to add and subtract single digit numbers.
Session Four
- Rename three digit numbers in many ways.
Session Five
- Break up hundreds and tens to rename amounts of money.
Our number system is very sophisticated though it may not look like it. While numbers are all around us in the environment, the meaning of digits in those numbers and the quantities they represent are challenging to understand. Our number system is based on groupings of ten. Ten ones form one ten, ten tens form one hundred, ten hundreds form one thousand. And so the system continues to represent very large numbers.
To represent all the numbers we use just ten digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The word for digits also comes from our fingers. We don’t need a new number to represent ten because we think of it as one set of hands, one group of ten. Similarly when we add one to 99 we write 100 and do not need a separate symbol for one hundred. The position of the 1 in 100 tells us about the value it represents. Zero has two uses in the number system, as the number for ‘none of something’, e.g. 6 + 0 = 6, and as a place holder, e.g. 704. Place holder means it occupies a place or places so the reader knows the values represented by the other digits. In 500 zero is acting as a place holder in the tens and ones places.
Place value means that both the position of a digit as well as the value of that digit indicate what quantity it represents. In the number 273 the position of the 2 is in the hundreds column which means that it represents two hundred. Seven is in the tens column which means that it represents 7 units of ten, 70.
Renaming a number flexibly is important. In particular it is vital that students understand that when ten ones are created they form a unit of ten, and when ten tens are created they form a set of one hundred. For example, the answer to 210 + 390 is 6 hundreds since one ten and nine tens combine to form another hundred. Similarly when a unit of one hundred is ‘decomposed’ into tens the number looks different but still represents the same quantity. For example, 420 can be viewed as 4 hundreds and 2 tens, or 3 hundreds and 12 tens, or 2 hundreds and 22 tens, etc. Decomposing is used in subtraction problems such as 720 – 480 = □ where it is helpful to view 720 as 6 hundreds and 12 tens.
This unit can be differentiated by altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
- have students use a variety of models of two-digit numbers to support their thinking, as needed (such as bundles of sticks or play money)
- have students work first with materials where ones can be combined to make tens (such as bundles of sticks, unifix cubes or piles of stones/counters/shells) and progress to materials which represent tens and ones differently (such as place value blocks or money). It is important that individual students have the opportunity to ‘make ten’ and bundle their groupable materials up themselves
- provide word stories using two-digit numbers to promote problem solving skills
- mix up ‘up through tens’ and ‘back through tens’ number problems to encourage students to use the most efficient strategy
- provide opportunities for students to work together (mahi tahi) and in pairs of differing abilities (tuakana/teina)
Some of the activities in this unit can be adapted to use contexts and materials that are familiar and engaging for students. For example:
- use te reo Māori for counting numbers to reinforce the tens-based structure of numbers, for example 70 is 7 groups of ten or whitu tekau
- use environmental materials to model the tens and ones structure of two-digit numbers, such as piles of stones, acorns or shells.
- write two-digit word problems that connect with your students (for example, kai at a hangi or tui on kowhai trees).
- Groupable materials such as: iceblock sticks and rubber bands, unifix cubes, beans/counters/stones/shells and bags or kete (only one type of material is needed)
- Calculators
- Play Money (Material Master 4-9) 20 of each note per pair of students
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
- Wooden or whiteboard cubes to make dice.
This unit is targeted at Level 2 so students are expected to have experience at Level 1 including:
- Forward and backward number sequences to 100 at least
- Counting and forming sets of objects to 100 at least
- Reading and writing numbers to 100 at least
This unit builds on the unit Place value with two digit numbers, and it would be useful for students to have worked through that unit first. Some materials created for that unit will also be useful here.
Activity
Session One
In this session the students analyse an abridged game of Snakes and Ladders to determine the gains and losses from climbing a ladder or sliding down a snake.
- Show the students the first Snakes and Ladders board (page one) of Copymaster 1. Make sure students know how the game works, then ask.
How many squares would a player gain by landing on the ladder on square 20? - Look for students to use place value to work out the answer of 19 by counting squares. You may need to draw students’ attention to the rows of ten squares. Make the connection to a hundreds board to support their thinking if needed.
We are now going to look at some of the other snakes and ladders. - For each ladder climb or snake slide ask the students to work out:
How many squares would a player gain or lose by landing on the ladder or snake? - Look for your students to use the differences between digits rather than counting by tens and ones to find their answers. For example, the snake at the top left has the player sliding from 91 to 65. A slide of 30 would take them from 91 to 61, since the tens digit changes from 9 to 6 and 9 tens – 3 tens = 6 tens. Since 65 is four more than 61 the actual drop is 26 (four less than 30). You may need to use groupable materials to model the operations.

A beans and bags model of 91 – 30 = 61. Putting four beans back gives 65 so the amount taken is 26. - Challenge the students to work in pairs to work out the number of squares gained or lost by other ladders and snakes. Start with an expectation that students can solve the problems using numbers but allow students to use groupable materials if they need support. Look for:
- Do the students record the beginning and end numbers for a snake or ladder?
- Do they look for changes to the digits to work out the gains or losses?
- Do they apply basic facts to find the gains and losses, rather than rely on counting?
- Do they use strategies like tidy numbers, as with 91 - □ = 65?
- Gather the class together to discuss their strategies, using symbols, diagrams and groupable materials to represent the quantities involved. For example, here is a tidy number strategy illustrated on an empty number line.
Ask the students to play Snakes and Ladders in pairs or threes - a tuakana/teina model could work well here. Use wooden or whiteboard cubes as the dice, using stickers or whiteboard pens on each face to write on. Copymaster 1 gives the playing boards. Three options of board are available for differentiation. Note that each board requires a different set of numbers to be on the dice. Tell your students to use efficient ways to work out where they will land with each dice roll rather than simply counting by ones. Note that the numbers are slightly different to a standard Snakes and Ladder board - the player moves from left to right across each row rather than zigzagging their way up the board.
After they have played the game for a while challenge your students to work out the gains and losses for each ladder and snake on their board. Expect them to apply the strategies they learned in Part One and record those strategies with numbers, equations or diagrams.
Session Two
In this session students learn to represent two digit numbers using a non-proportional representation, play money (see Material Master 4-9 to make a set of play money. At this point you only need one hundred, ten, and one dollar notes.)
Part One
- Students need to be seated so they can all see an A3 sized place value mat (Copymaster 2). Each pair of students should have their groupable materials behind their backs for when they need them.
What is the amount of money that this note is representing? (Holding up $1 note) - Ask the students to count as you repeatedly place $1 notes in the ones column of the place value mat until you reach $9.
Now what happens next? - See if students realise you could just leave ten $1 notes in the ones place or you could exchange those notes for one $10 note. Let a student act as ‘the bank’ as you exchange the money and place a single $10 note in the tens column.
How do I write this amount of money? ($10 though some students will know about the decimal point). - Build up the teen numbers by adding $1 notes to the ones place until $19 is reached.
What happens now? (Adding one $1 note gives ten $1 notes in the ones place that can be exchanged for one $10 note) - Tell the students that you are going to show them amounts of money on the place value mat. Their job is to represent the same number of groupable objects as there are dollars. The purpose of doing this is to help students recognise that within a ten dollar note are ten ‘objects’, dollars. You might use examples like; $17, $28, $53, $67, $95. Below $95 is represented by nine $10 notes and five $1 notes with the matching representation with beans in bags.
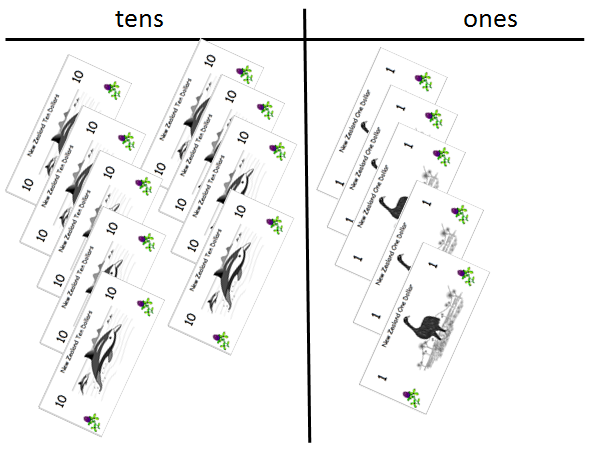
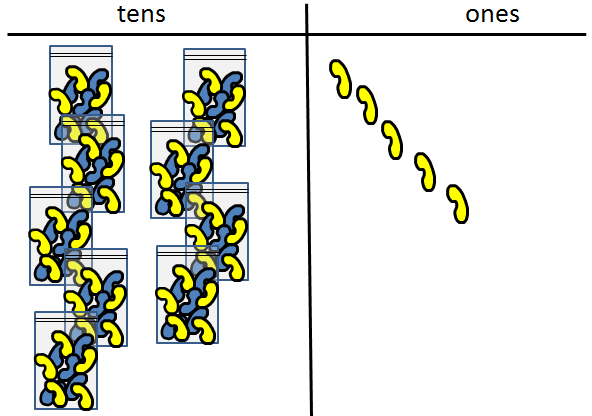
- Use counting to represent the link between changes in the symbols and changes in quantity, both with money and with the grouped objects. Good sequences might be:
14, 24, 34, 44, 54, …, 94, … What happens next?
87, 77, 67, 57,…, 17, … What happens next?
95, 96, 97, 98, 99, … What happens next? - In the first sequence ten $10 notes are exchanged for one $100 note and a new column on the place value mat is needed (see Copymaster 2 – enlarge to A3). The second sequence is interesting because ten dollars can only by subtracted until $7 is reached though some students might propose negative $3, like a debt. This is an opportunity for differentiation if it occurs.
- In the third sequence two exchanges are needed. Ten $1 notes can be exchanged for one $10 note then there are ten $10 notes. These ten notes can be exchanged for one $100 note. Then counting by ones can continue; 100, 101, 102, 103,…
- Note that students might recognise that their groupable object representation is different to the money in that no exchanges are needed. They simply need to repackage ten tens as a unit of one hundred. You may find suitable containers to house ten tens, and use that as a representation of one hundred. For example, large kete, ice cream containers or big rubber bands.
Pay Me is a task in which students make up the pay for employees. You will need:
- a lot of envelopes, preferably recycled from the school office
- at least 30 of each note ($10 and $1) and about ten $100 notes per group. $100 notes are useful if you want to extend the activity for some students and for later work on place value.
- Copymaster 3 for the students, with one challenge per group of students.
There are two different versions of Pay Me at varying degrees of complexity:
- Making up two digit whole numbers with money, though exchanging with the bank is challenging
- Combining two digit amounts of money before paying, with exchange as well
The task is worked through in groups of three students. One student becomes the banker who exchanges notes and checks the pay envelopes for accuracy. Two students work together on creating the pay envelopes. Copymaster 3 has a set of instructions at the bottom of each page about what amount to start with and instructions about putting a pay slip in each envelope. Students cut out each pay slip and put it into an envelope with the correct amount. You might also ask them to write the amount in words though that can restrict the participation of some students. The Banker checks to see that the amount is correct. Each set of slips has a final question that students should answer to show they have completed the task correctly. Look for:
- Do the students represent each amount correctly?
- Do they exchange notes correctly with an expectation of how much money they will have after the exchange?
- Do they use place value to add and subtract amounts where required?
After the students have completed the task bring them together to share what they learned. You might like to pose other challenges for assessment purposes:
- Melissa earns $72 and has to pay $20 in tax. How much money should go in her pay envelope?
- Hone earns $35 on one job and $47 on another job. How much money should go in his pay envelope?
Session Three
In this session the students gain fluency in using ‘up through ten’ and ‘back through ten’ strategies for addition and subtraction.
- Either use a set of playing cards with the picture cards and joker removed, or create a set of digit cards using Copymaster 4. Each pair of students will need groupable objects or play money behind them. Allow them to choose which representation they prefer.
- Write these two digit numbers of the board: 12, 20, 34, 45, 51, 67, 73, 86, 90, 100
- Tell the students that the first activity is a class challenge.
Each time we make one of these totals our class scores 10 points. - The game is simple. A deck of digit cards is shuffled and placed in the middle beside the place value mat (Copymaster 2). Someone turns over the top card and that number of objects is added to what is already there. If a zero (or ten with playing cards) comes up someone gets to choose a single digit number to add.
- Draw the first card, say 3 comes up. The students get three objects or three $1 notes.
- Draw the next card, say 9 comes up. The students get nine objects or nine $1 notes and add them to their collection. Expect the students to form a ten with ten of the objects, or exchange ten $1 notes for a $10 note. The total in this case is 12 so the class gets a point as 12 is a target number.
- Draw the third card, say 0 comes up. A student is chosen to decide what will be added on. They choose 8 so the total is 20, also a target number. Again ten ones will need to be regrouped as one ten or exchanged for one $10 note.
- Play continues like that with the class getting ten points for every target number scored and ten tens being exchanged for one hundred. It is important during the game that students anticipate the result of adding one before physically doing the addition. Anticipation will promote ‘up over ten’ strategies.
- Look to see that students are anticipating the result of adding the card number, carrying out correct exchanges with their money or groupable materials, and thinking ahead to the next target number. You might also choose to capture the additions using the empty number line learning object. For example:
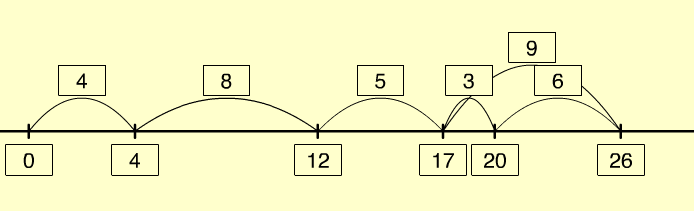
- The target game can be played backwards by starting with 100 and taking away the card number. This will help practice ‘back through ten’ strategies, such as 83 – 7 = □ as 83 – 3 = 80, 80 – 4 = 76.
- Play the game Race to 100 in pairs. Students need a calculator to share. The first player enters a single digit number other than zero, say 4. The second player adds a single digit number other than zero to get a new total, say adds 5 to get 9. The first player goes next, adding a single digit number, then player two adds a single digit number, etc.
- Play continues like that until either of two things happen:
- A player gets the total to exactly 100 (They win).
- A player gets the total over 100 (They lose).
- Before the students go away, challenge them to find a strategy to win the game. It is also important that they take turns to start the game.
I want you to think ahead about what the total will be when you add a number. Is there a way to always win or is it just good luck? Does it matter who goes first? - Let the students play while you watch for:
- Do the students anticipate the total before they add a number?
- Are they looking for a winning strategy?
- A winning strategy may not be found which means the game can remain a challenge for a few days. Students can also play racing down to zero, starting at 100, and taking away single digit numbers. A winning strategy is to be the second player and ‘cover your opponent’ to the next decade.
- Consider this sequence of moves.
- When Player One enters three, Player Two adds seven to make ten.
- When Player One adds six to get 16, Player Two adds four to make the next decade, 20.
- When Player One adds eight to get 28, Player Two adds two to make the next decade, 30.
- If Player Two responds by adding the number needed to make the next decade they must always win, since 100 is a multiple of ten.
- If students do discover a winning strategy, change the target number to see how they respond. Having a target like 123 is a good extension. You might also ‘disable’ keys other than zero.
Suppose 0, 2 and 7 did not work. How would that change your strategy?
Session Four
In this session the students explore the place value of 3 digit whole numbers, particularly building up tens to make hundreds.
You will need about 500 groupable objects, hopefully still organised into tens and ones. You will need a way to collect ten tens into one hundred. For example, a large kete, ice cream container or bigger ribber bands. You will also need a place value mat (Copymaster 2) enlarged to A3 size.
- Students need to work in pairs (a tuakana/teina model could work here) with a set of play money and an A3 size photocopy of the place value mat to organise their materials. In this part of the lesson you build up numbers with the groupable objects and the students replicate the amount with play money. It is also important to discuss changes to the numbers as the amount changes.
- Build up the groupable objects in this way, expecting students to match the amount with play money, and using an online calculator to show the numbers.
- Put nine single objects in the ones column of the place value mat.
What number have I made? Make that amount with play money.
If I add one more dollar what happens then? Show me with your play money.
Why does the calculator use a zero here (10)? - Expect students to collect ten one dollar notes and exchange those notes for a single ten dollar note. With the groupable objects you bundle the ones into a single ten and shift it to the tens place.
I am adding one, two, three,…, seven, eight, nine ones (Count them out as you add them). What is the number now? What happens if I add one? How does the number 19 change when I add one? - Build up two digit numbers expecting students to repeat the changes and exchanges with their play money. Ask if they can anticipate the changes to the numbers on the calculator.
Progress in this sequence:- 20 then add nine to make 29
- 29 then add one to make 30
- 30 then add 20 to make 50
- 50 then add 9 to make 59
- 59 then add one to make 60 then add 30 to make 90
- 90 then add nine to make 99
- 99 then add one to make 100 (note the two bundlings, ten ones become one ten then ten tens become 100)
Why does the calculator use two zeros to show 100?
- Once 100 is reached you can move more rapidly into three digit numbers. Here is a sequence you might use:
100 → 109 (Why a zero in the tens column?) → 110 (Why a zero in the ones column?) → 150 (Why does the ones digit not change?) → 198 → 200 (Two acts of rebundling or exchanging) → 204 → 214 → 294 → 300 → 305 → …etc.
An issue with the use of zero as a place holder is that the way numbers appear creates an impression that there are no units of a given place value in a number, e.g. 204 has no tens. A flexible understanding of place value is essential for calculation. In particular, knowing that ones are nested within tens, and tens are nested within hundreds is very important. So there are actually 20 tens in 204. This activity helps students rename three digit numbers in multiple ways.
- Tell the students that their group will get a ‘price tag’ item (See Copymaster 5). For example the item might cost $247.
How could I pay for this item with play money? - Students are likely to suggest two $100 notes, four $10 notes and seven $1 notes. Challenge them to think about other ways to make up that amount.
What if the cash machine only gave out $10 and $1 notes? How could I make $247? - Students might need to build up the amount counting in tens, i.e. 10, 20, 30… Encourage them to ‘short-cut’ the counting process with questions like:
How many $10 notes make $100? How many $10 notes make $200? How many $10 notes make $240? How many extra $1 notes will you need?
Could I make $247 with only one $100 note and $10 and $1 notes? How? - Tell the students that they need to work out many different ways to pay for the ‘price tag’ item they get. Discuss efficient ways to record their ways. Diagrams and symbols are useful.
- Send the groups away to work (mahi tahi) on their ‘price tag’ item. You can vary the difficulty of the challenge by choosing which item to give to each group. Students could also write their own 'price tag' items. Look for students to:
- Correctly create a money amount that matches the price tag
- Rename place value units to create the amount in different ways
- Record the combinations of notes efficiently
- After the students have created many ways to ‘pay’ for their item, bring the class together to discuss the strategies they used. Highlight point two above. For example, if a $274 family ticket to Te Puia springs can be paid for with 2 x $100, 7 x $10, and 4 x $1 notes, a $100 note can be exchanged for ten $10 notes to make 1 x $100, 17 x $10, and 4 x $1 notes. One $10 note might be exchanged for ten $1 notes, etc.
Session Five
In this session students extend their understanding of three digit whole numbers to include ‘breaking up’ of hundreds and tens units.
Use the ‘Modeling three digit numbers’ digital learning object. As with the previous day students work in pairs with a set of play money and a place value mat.
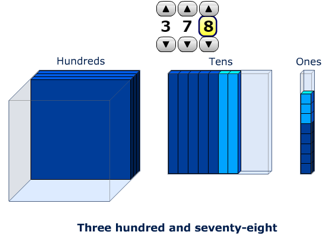
- The learning object uses a place value block model to represent three digit numbers and contains other options for the symbolic representations, such as compact numerals, words and voice. Create a few different three digit numbers on the learning object and expect the student to replicate that amount and the operations with play money. For example, here is the number 378 modeled:
How many tens are in 378? (Students may say 7 which is correct to the place values but there are also 30 tens in 300)
If I added three ones, what would happen? (two added ones would form a set of ten ones that would combine to form a ten unit and move places. Adding another one would result in 381)
If I next added three tens what would happen? (Two more tens would create ten tens which would combine to form one hundred and move places. Another ten more would result in 411) - Use other examples like:
399 + 1 = 400, 400 + 7 = 407, 407 + 90 = 497, 497 + 3 = 500, … - After a few examples of ‘building up’ place values, progress to ‘breaking down’ place values. Begin with the numbers 426 modeled on the learning object:
What would happen if I took seven ones away? (Taking away six ones leaves 420 but to take another one away (click on the down arrow) would require one ten to be ‘broken up’ into ten ones and moved into the ones column. Removing one would leave 419).
What would happen if I took two tens away? (Taking away 19 would leave 400. To take one more away would result in two ‘break up’ actions. One hundred would become ten tens and move columns. One ten would become ten ones and move columns. One would be removed leaving 399). - Use other examples like this:
183 – 4 = 179, 179 – 90 = 89, 89 – 10 = 79,…
302 – 20 = 282, 282 – 100 = 182, 182 – 80 = 102, 102 – 3 = 99,… - Look for students to exchange notes to match what occurs with the learning object. Students could use the digital learning object independently to explore three-digit numbers and beyond.
- To practice ‘breaking down’ place values, tell the students to play a game of Bankrupt, a game in which you lose money until you have none. To play the game the students need play money, a calculator, and two dice. One dice is standard (1-6) and the other dice has these words on the faces; hundreds, tens, tens, ones, choose, choose. The game can be played in groups of four with one player being the banker. Swap roles for a new game. Encourage the students to record the transactions.
All students start with $800 (8 x $100 notes). They take turns to:
- Roll both dice. The dice tell how much money is being lost, e.g. 4 tens means $40 is taken away. If ‘choose’ comes up the student can choose whether hundreds, tens or ones are subtracted.
- Predict how much money they will have left then carry out the operation with their play money. Note that students will often have to exchange money with the bank.
- Another player checks the operation on a calculator to ensure it is correct.
The first person to lose all of their money exactly is the winner. They cannot lose more than what they have left.
- Look for the following:
- Do the students correctly anticipate the results of the subtraction?
- Do they recognise when breaking down of a place value unit is needed?
- Do they apply basic facts to place value units rather than rely on counting back?, e.g. 500 – 400 = 100 since 5 – 4 = 1.
- After a suitable period of playing, bring the students together on the mat. Discuss the points above using student’s record of a game as an example.
Dear whānau,
At school we have been learning to add and subtract two-digit and three-digit numbers. Please support your child at home by using junk mail from the letterbox or other advertisements to add and subtract items that are for sale. For example, you could circle 2 or 3 items from a supermarket mailer and your child could explain how to add up the total cost. Or, you could pretend they had $100 to spend at the local market and see how much money they would have left over after buying some items your whānau usually buys.