This collection of learning activities is designed to provide engaging contexts in which to explore the achievement objectives from Level 3 of the NZC. The activities themselves do not represent a complete coverage of learning at this level. Rather they provide an opportunity to apply the mathematics learned in previous lessons. The activities are intended to reflect the range of approaches that make up a differentiated classroom. (show more)
In the delivery of the Mathematics and Statistics learning area of the NZC, students should be exposed to a variety of teaching and learning strategies. While we can't expect them to synthesise to the extent that they are 'reinventing the wheel', they should be given opportunities to derive and to feel an ownership of their mathematics. This can occur with a careful balance of:
- introducing 'building blocks' of knowledge, skills and techniques (teacher-driven including discussion, examples, notes)
- building skills, confidence and competence with 'reinforcement' exercises, where the students are employing a method they have been shown to solve a series of similar problems (text books or worksheets)
- building an understanding of mathematical thinking, with structured investigations, proof work and open-ended problem solving. Examples of these activities are given in the rich learning activities.
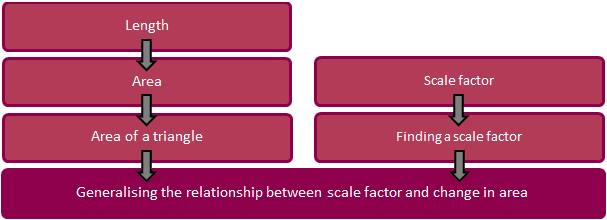
The sequence of knowledge and skills needed for a rich learning activity are shown in flow chart format, under the heading 'Description of Mathematics' in each activity. An example of the teaching and learning that should occur before students would be given the Bigger Triangles activity follows.
The 'building blocks' and reinforcement exercises that will prepare the student for this rich learning activity (Bigger Triangles) are shown in a suggested order of treatment below.
These rich learning activities have been constructed for use with students working at NZC Level 3. The types of thinking employed by students in the process of attempting these activities are a consequence of their skill and familiarity with the processes they have mastered in mathematics. At any particular point in time, a typical class might have students falling into several different groupings of approach to problem solving. Whilst the students can all be given the same problem to solve, it is unlikely that they would all attempt to solve the problem using the same process. The teacher may take different approaches in guiding each student towards success in solving the problem, but without removing their opportunity for ownership of the solution. Prompts the teacher might give, have been broken down into categories appropriate to the nature of the achievement objective and the activity at hand.
- The arithmetic approach: recognises that students may be very capable numerically but not necessarily so confident in their independent use of algebra when solving problems. Often they appreciate seeing a numerical example or model to accept a process. Classroom observation can help identify students who are taking such an approach to their mathematical exploration. These are the students who might:
- initially try to solve a problem with 'guess and check' techniques.
- appreciate being given numerically equivalent statements to illustrate a concept.
- The procedural approach: is aimed at students who are competent numerically and algebraically and are able to use algebra as a tool to solve defined problems. These are the students who might:
- solve problems by following familiar processes.
- appreciate having new concepts explained by appealing to familiar rules.
The conceptual approach: attempts to develop and extend the skills of students who can apply the tools of algebra, with abstract thinking to generalise. These are the students who:
- make the link between calculation and context.
- can independently construct equations to represent mathematical information.
- can link mathematical ideas to form a reasoned argument.
- understand when all the possible solutions to a problem have been found.
Students who are able to solve problems in this manner are often, but not always, those identified as needing extension work because they are quick to 'get' a new concept. Rather than being given more work, or being introduced to further concepts (including those from higher levels of the NZC), they should be given the opportunity to develop the depth of their thinking and reasoning and the chance to synthesise. The skills they can be encouraged to develop, by following the 'conceptual' approach, form the foundations of the abstract thinking required for excellence in NCEA mathematics and for successful application of mathematics beyond.
In all the approaches outlined above, the students should be working at Level 3 of the NZC, covering the concepts and processes outlined in the AOs. As a student develops their ability to generalise to devise a solution or method of solution and/or to choose the most effective tools for the problem at hand, they may very well follow a different approach. It is therefore important to avoid labelling a student, for example, as 'arithmetic'.
