New Zealand Curriculum: Level 3 to early Level 4
Learning Progression Frameworks: Measurement sense, Signpost 5 to Signpost 7
Target students
These activities are intended for students who understand how to use units of measure to find length and areas of rectangles. They should understand the following:
- Units relate to the attribute being measured (for example, area is measured with iterations of area).
- Identical units need to be used when measuring.
- Units should be tiled (or iterated) with no gaps or overlaps to create a measure.
- Units can be equally partitioned into smaller units when greater accuracy is needed.
Students should also know how to use a measurement scale, such as a ruler or tape measure. They should be familiar with the common metric units of length, metres, centimetres, and possibly millimetres, though they may not be able to convert measures (e.g., 45cm = 450mm). Students should have a partial or full grasp of their basic multiplication facts and the division equivalents.
The following diagnostic questions indicate students’ understanding of, and ability to find the volumes and surface area of cuboids (rectangular prisms). Allow access to pencils, paper and to a calculator if needed (show diagnostic questions).
The questions should be presented orally and in a written form so that the student can refer to them. The questions have been posed without context but can be changed to other contexts that are engaging to your students.
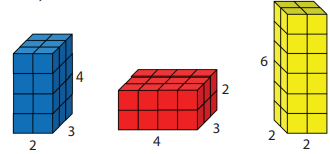
- Here are three different cuboids. The shapes are also called rectangular prisms. The numbers show how many blocks are on each edge.
How many small cubes are in each of these cuboids?
Signs of fluency and understanding:
Uses multiplication to count the number of small cubes, for example 2 x 3 x 4 = 24 for the blue cuboid. Recognises that the product of edge lengths gives the number of small cubes.
May notice that the blue and red cuboids have the same edge length and therefore have the same volume. The blue and red cuboids are the same cuboid in different orientations.
What to notice if they don’t solve the problem fluently:
Counts, in ones, or skip counts in twos, to find the total number of small cubes in each layer. This indicates an inability to structure the cuboid in ‘layers or slices’. It may also indicate a lack of recognition that multiplication can be used to count the number of small cubes.
Supporting activity:
Finding volumes of cuboids (whole number edge lengths)
- Measure the edges of each cuboid shaped box in centimetres. Write the measurements down. Use the measurements to work out the volume of each box in cubic centimetres. Write the volumes using both numbers and units.
[Provide students with two small cuboid boxes and a calculator. The edge lengths of the boxes should be whole numbers of centimetres.]
Signs of fluency and understanding:
Measures the edge lengths accurately to the nearest centimetre and writes the measures using correct units. Applies multiplication to find and record the volumes, i.e., 14 x 4 x 12 = 672cm3.
What to notice if they don’t solve the problem fluently:
Draws in or images marks to partition each edge into cubic units of 1cm3 before finding a way to count all the small cubes. This indicates an inability to anticipate the structure of a cuboid in a 3-dimensional array of small cubes.
Applies additive strategies to find the number of cubic units, such as imagining a layer or ‘tower’ of cubic units and fitting the layers or towers into the cuboid by addition. For example, a tower is 12 cubes so 12 + 12 + 12 + 12 = 48 makes a vertical layer. Adding 12 + 12 + 12 … (14 times) gives the volume. Use of this strategy might indicate that the student has yet to establish multiplication as a binary (two numbers at a time) operation or connect multiplication with the structure of 3-dimensional arrays.
Use of either of these strategies is likely to be extremally time consuming and cumbersome. You may like to intervene and encourage the student to use a more efficient strategy.
Supporting activity:
Finding the volumes of cuboids by measuring edge lengths.
- This cuboid has a volume of 3 x 8 x 4 = 96cm3. The numbers show the length of each edge.
What is the surface area of the cuboid?
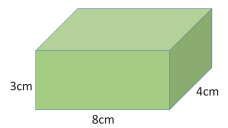
Have a calculator available. Ask students to record information and draw diagrams. You may need to explain that surface area is the sum of the areas of all the faces.
Signs of fluency and understanding:
Calculates the area of each rectangular face using multiplication, possibly using a calculator. Adds the areas of the rectangles using an efficient mental, written, or calculator-aided method. For example, 3 x 8 = 24cm2, 4 x 8 = 32cm2, 3 x 4 = 12 cm2, and 24 + 32 + 12 + 24 + 32 + 12 = 136cm2.
Students may notice identical parallel faces and multiply 2 x (24 + 32 + 12) = 136cm2.
What to notice if they don’t solve the problem fluently:
Uses multiplication to find the area of each face but does not not account for all faces. This suggests that the student needs to develop their understanding of the structure of cuboids, such as recognising that they have six rectangular faces, 3 pairs of identical parallel faces, and that the rectangles have side lengths that are pairs formed from the three dimensions.
Supporting activity:
Finding surface areas
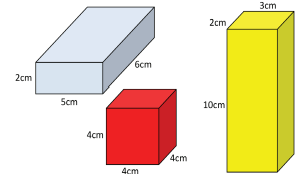
Which cuboid has the greatest volume? Which shape has the greatest surface area?
Signs of fluency and understanding:
Calculates the volume and surface area of each cuboid using multiplication and addition, as appropriate. May use mental and paper calculation or a calculator combined with recording on paper. For example, the volume of the yellow cuboid can be calculated as 2 x 3 x 10 = 60cm3 and the surface area as 2 x (6 + 20 + 30) = 112cm2.
Recognises that surface area and volume are different attributes, meaning the measures are expressed using different units: area units for surface area (cm2) and cubic units for volume (cm3).
Answers:
| Cuboid | Dimensions | Volume | Surface area |
| Blue | 2cm x 5cm x 6cm | 60cm3 | 104cm2 |
| Red | 4cm x 4cm x 4cm | 64cm3 | 96cm2 |
| Yellow | 2cm x 3cm x 10cm | 60cm3 | 112cm2 |
What to notice if they don’t solve the problem fluently:
May confuse the two attributes, volume and surface area, when providing answers.
May have difficulty coordinating the information from the diagram to make appropriate calculations. This suggests that the student needs more experience representing 3-dimensional models of cuboids with 2-dimensional diagrams.
Supporting activity:
Working with volume and surface area together
- Use a ruler to measure the edge lengths first then find the volume and surface area of this box using a calculator.
[Provide students with a small grocery box that has edge lengths that are not all whole numbers, such as 20cm x 7.5cm x 6.3cm].
Signs of fluency and understanding:
Measures the edge lengths accurately and expresses the lengths as decimals, e.g., 18.5cm, 11.3cm, and 7.2cm.
Correctly applies an appropriate algorithm to find both the volume and the surface area. Volume can be calculated as 18.5 x 11.3 x 7.2 = 1567.785cm3. Surface area can be calculated by finding the area of all three pairs of faces (using multiplication) then combining the measures to get a total.
Demonstrates understanding of the size of the units by including the number and unit of measure, and by explaining the size and nature of the unit, i.e., 1cm3 is a cube that is 1cm x 1cm x 1cm.
What to notice if they don’t solve the problem fluently:
May be unsure about how to accommodate, or operate on, decimal numbers of measurement units. This is likely to show as being unsure of how to express edge lengths, such as 18.5cm, 11.3cm and 7.2cm respectively. This indicates that the student needs experience with measuring lengths with greater accuracy using smaller units in the metric system.
May measure the side lengths accurately but be unclear about how to find the volume and surface area by calculation. They may also express the resulting measure using appropriate units. This indicates the student needs more experience using partial units when calculating volumes and surface areas.
Supporting activity:
Finding volumes and surface areas from decimal side lengths
Teaching activities


