The purpose of this activity is to support students in distinguishing between the surface area and volume of cuboids. Students use multiplicative methods for finding the measurements, and record the measurements using appropriate units (square centimetres (cm2) for surface area and cubic centimetres (cm3) for volume). Students also need to develop a sense of size for important multiples of these units, such as 1000cm3 and 100cm2.
- Connecting cubes 2cm x 2cm x 2cm
- Calculators (if needed)
- Present students with a group of 60 connecting cubes and ask them to count them, or tell them the total number of cubes. This might be a good opportunity to consolidate your students' use of additive and/or multiplicative strategies.
- Tell students a definition of volume (rōrahi), for example "volume is the measure of space taken up by a three-dimensional object."
What is the total volume of all 60 cubes in cubic centimetres?
First establish that each cube measures 2cm x 2cm x 2cm, meaning that each cube has a volume of 8cm3. You might use 8 place value unit cubes to confirm this. Therefore, 60 cubes have a volume of 60 x 8 = 480 cm3. Compare that volume to a litre (1000 cm3).
You are working with volumes of just under half one litre.
- Ask students to make different sized cuboids that contain exactly 60 connecting cubes so have a volume of 480cm3.
Let’s see how many cuboids we can make. How can you record the different cuboids you find?
Organise students in groupings that will encourage peer scaffolding and extension, as well as productive learning conversations. Together, you might make a shared list of methods for recording the cuboids.
Roam as students work and look for students to:- anticipate dimensions that will work using calculation and diagrams.
- apply multiplicative thinking to find possible dimensions. For example, if the length is set at 20cm then each vertical layer must have 480 ÷ 20 = 24 cm3.
- Gather the group and discuss the cuboids that have been made.
Are these cuboids distinct? That means they are different in their dimensions - they are not just turned around or flipped copies.
Create a group collection of cuboids (physical models). Express the dimensions in centimetres. Examples might be: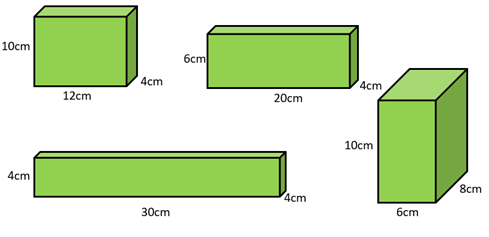
Have we found all the possibilities? How do you know?
The prime factors of 60 are 2 x 2 x 3 x 5. Considering all the possible trios formed from these factors gives all the cuboids that can be made.
In the examples above the possibility of having 2cm as a dimension has not been considered. Using 2cm as a dimension gives six other possible cuboids:- 2cm x 2cm x 120cm
- 2cm x 4cm x 60cm
- 2cm x 6cm x 40cm
- 2cm x 8cm x 30cm
- 2cm x 10cm x 24cm
- 2cm x 12cm x 20cm.
If you have sufficient cubes, make all the 10 possible unique models (as above).
All these cuboids have the same volume. Do they have the same surface area?
Let students discuss the question and come to a consensus about surface areas.
Allocate the cuboids and ask the students to use their rulers and calculators to find the surface areas. Organise the data in a table, as shown below:
Dimensions (cm) Calculation for surface area Surface area (cm2) 4x12x10 2x (4x12+4x10+12x10) 416cm2 4x4x30 2x (4x4+4x30+4x30) 512cm2 4x20x6 2x (4x20+4x6+20x6) 448cm2 6x8x10 2x (6x8+6x10+8x10) 376cm2 2x2x120 2x (2x2+2x120+2x120) 968cm2 2x4x60 2x (2x4+2x60+4x60) 736cm2 2x6x40 2x (2x6+2x40+6x40) 664cm2 2x8x30 2x (2x8+2x30+8x30) 632cm2 2x10x24 2x (2x10+2x24+10x24) 616cm2 2x12x20 2x (2x12+2x20+12x20) 608cm2 - What do you notice?
Students should comment that cuboids with equal volume need not have equal surface area. Some may notice that long, thin cuboids have greater surface areas than those with dimensions that are similar lengths, such as 6cm x 8cm x 10cm.
Next steps
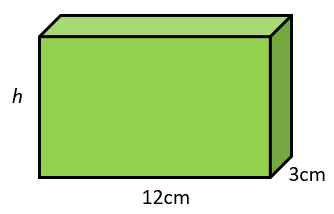
- Extend interpretation of volume and surface area with problems where surface area or volume is given but a dimension (edge length) is not. Two examples might be:
- The surface area is 312 cm2. What is the dimension labelled h?
- The volume of the cuboid is 420cm3. The surface area is 349cm2.
What is dimension (edge length) marked l?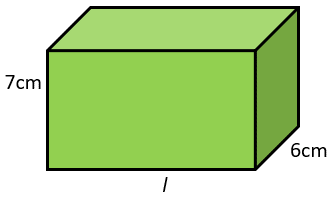
- The surface area is 312 cm2. What is the dimension labelled h?