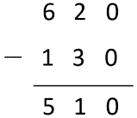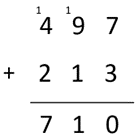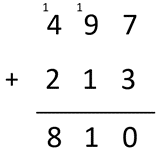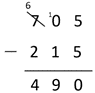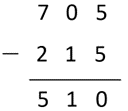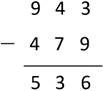New Zealand Curriculum: Level 2 to Level 3
Learning Progression Frameworks: Additive Thinking, Signpost 6 to Signpost 7
Target students
These activities are intended for students who understand place value with two- and three-digit numbers but are not yet able to use this knowledge to solve addition and subtraction problems. While these activities assume students know most of their addition and subtraction basic facts (number bonds to 20), some students may need support to revise or develop these. For students who are not yet able to use place value to solve two-digit addition and subtraction problems see Using whole number place value for two-digit addition and subtraction.
The following diagnostic problems indicate students’ understanding of, and ability to use, place value to add and subtract whole numbers to three places. The problems are presented in order of complexity. Avoid asking a problem if the student has found the previous problem difficult. (show diagnostic questions)
Present the problems orally and in written form to provide a resource for students to refer to as they work. You might change the objects or contexts in the problems to suit the interests of your students. Allow access to pencil and paper but not to a calculator.
- There are 500 people in the town. 460 more people come to the town for the holidays.
How many people are in the town now?
Signs of fluency and understanding:
Recognises that the hundred units 500 and 400 combine to form 900, then adds 60 to make a total of 960. Shows clear understanding of the place value of each digit.
Using a written algorithm does not necessarily indicate understanding of place value. Ask students who use a written algorithm to explain the meaning of each digit.
What to notice if they don’t solve the problem fluently:
Counts on in hundreds, 500, 600, 700, 800, 900, then in units of ten, 900, 910, 920, 930, 940, 950, 960. This indicates that the student has control of some counting sequences, but does not yet understand that units of ten and hundred can be added in the same way as ones can be added.
Unable to obtain an answer or confuses place values to get answers like 546. This indicates that the student needs to develop understanding of place value of three-digit whole numbers.
Supporting activity:
Addition with hundreds and tens
- There are 620 people at the netball game. 130 people leave early.
How many people are left at the game?
Signs of fluency and understanding:
Recognises that the subtracting 120 people from 620 leaves 500 people, then subtracts ten to get 490 people left at the game. This indicates that the student has solid understanding that ten tens make 100.
Using a written algorithm that does not necessarily indicate understanding of place value. Ask students who use a written algorithm to explain the meaning of each digit.
The algorithm involves renaming so ask the student about their working to see they can explain that 100 can be decomposed into ten tens.
What to notice if they don’t solve the problem fluently:
Counts backward in hundreds first, 520, 420, then tens, 420, 410,400, 390. This indicates that the student has control of some backward counting sequences, but does not yet understand that units of ten and hundred can be subtracted in the same way ones can be. They may also not realise that 100 can be decomposed into ten tens.
Uses lower from higher in each place value column, often associated with a written algorithm. For example, in the tens place subtracts 30 – 20 = 10 rather than 20 – 30.
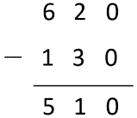
This indicates that the student needs experience with connecting their calculations to changes in quantities, modelled with place value materials.
Supporting activity:
Subtraction with hundreds and tens
- 497 people are at the concert. 213 more people come along.
How many people are at the concert now?
Signs of fluency and understanding:
Uses an efficient place value-based mental calculation. This might involve renaming the calculation as 500 + 210 by moving three from the 213 onto the 497.
Records working as an algorithm or an empty number line.
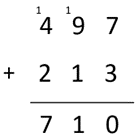
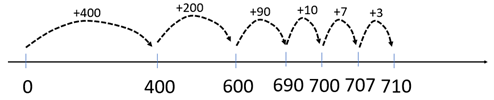
Neither strategy is efficient but may show understanding of place value if the student can explain the renaming of ten tens as one hundred.
What to notice if they don’t solve the problem fluently:
Gets lost in the working due to excessive load on working memory. This may happen when a student attempts a mental strategy that inefficiently combines place value units (see the number line above). This suggests that the student needs support with recording their working to reduce the memory load.
Performs an algorithm with errors and does not recognise the unreasonableness of the answer. For example:
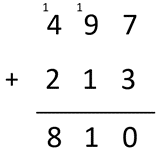
This suggests that the student needs to work with materials and the written algorithm simultaneously, so they understand what the manipulation of numbers means for the quantities involved.
Supporting activity:
Addition with renaming
There are usually 705 students at the school. 215 students are away today with ill-health.
How many students are at the school today?
Signs of fluency and understanding:
Uses an efficient place value-based mental calculation. This often involves one of the following:
- Subtracting 200 to get 505 then subtracting 15 to get 490.
- Subtracting 5 from both numbers first to get 700 – 210 then subtracting 200 then subtracting 10.
Records working as an algorithm or an empty number line.
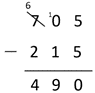
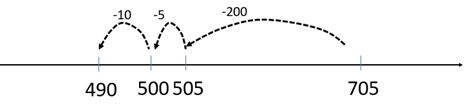
Both strategies are moderately efficient but ask the student to explain the meaning of the digits in the algorithm or to explain the jumps on the empty number line.
What to notice if they don’t solve the problem fluently:
Gets lost in the working due to excessive load on working memory. This frequently happens when a student attempts a mental strategy that inefficiently combines place value units (see number line above). This suggests that a need to support the use of logical, systematic recording to ease mental load, such as using empty number lines or algorithms.
Performs an algorithm with errors and does not recognise the unreasonableness of the answer. The most common error is to take smaller from bigger. For example:
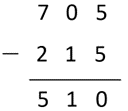
This suggests that the student needs to work with materials and the written algorithm simultaneously, so they understand what the manipulation of numbers means for the quantities involved.
Supporting activity:
Subtraction with renaming in one place
- There are 943 students at Rere School and 479 students at Kopu School.
How many more students are at Rere School than Kopu School?
Signs of fluency and understanding:
Recognises that the problem can be solved by either subtracting 479 from 943 or adding onto 479 to make 943. Obtains the correct answer (464).
Uses a systematic, logical form of recording to manage the memory load of renaming numbers. This might include using an empty number line or algorithm.
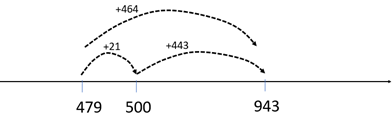
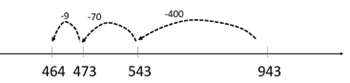

Another manageable mental strategy could be rounding and adjusting the answer, such as 943 – 500 + 21, or 950 – 480 – 7 + 1. Such strategies demonstrate strong understanding of place value and difference and indicate excellent working memory.
What to notice if they don’t solve the problem fluently:
Unable to create an operation to solve the problem. This indicates that the student needs more experience with difference problems.
Gets lost in the working due to excessive load on working memory. This frequently happens when the student attempts a mental strategy that combines place value units inefficiently (see number line above). This suggests the student needs support to use recording, as a way of easing mental load, such as empty number lines or algorithms.
Performs an algorithm with errors and does not recognise the unreasonableness of the answer. The common error is to take smaller from bigger. For example:
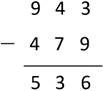
This suggests that the student needs to work with materials and the written algorithm simultaneously, so they understand what the manipulation of numbers means for the quantities involved.
Supporting activity:
Difference with renaming in two places
Teaching activities