What's going on? Fractions

All lessons in this unit follow the same sequence of phases as given in the diagram above. A poster of the phases is provided as Copymaster 1 for students to refer to. The notes suggest possible student ideas and teacher reactions to those responses. It is not feasible to anticipate all ideas students might give so you are encouraged to be flexible in how you respond to students rather than ‘teach’ the sample ideas and representations provided.

PowerPoint 1 gives the equation sets that drive the unit. The sets are labelled in the top left corner of each slide for reference. Slide One has the first pattern to look at. The pattern involves the addition of fractions with the same denominator i.e., 1/b + (b-1)/b = 1, 1/3 + 2/3 = 1. These patterns will be, relatively easy for students to represent. Slide One can be used as an example to familiarise students with the approach. Be aware that students’ existing schemes for addition of fractions may be incorrect, e.g., they may simply add across the numerators and denominators:1/4 + 3/4 = 4/8.

Equation Pairs Set One

Noticing Consistency

Use ‘think, pair, share’ by inviting students to look independently at the four examples, work out the missing values, then share their ideas with a partner. In the class discussion expect students to express their observations in ways that are clear to others. Students should re-express their ideas if others do not understand what they are saying. You may need to remind students that the ‘something going on’ relates to all four examples, not just one. Expect responses like:

S: The first fraction always has one on the top line.

T: Can you tell us more? What is the denominator, the bottom number?

S: The bottom numbers, denominators are different in each equation.

Discussion opens the possibility of using correct mathematical terms, like numerator (number above the vinculum), and denominator (number below the vinculum).

S: The sum (answer) is always one.

T: All four equations have a sum of one? What about the top right equation?

S: The sum is five fifths. Five fifths make one whole.

Making a claim

Encourage students to state a claim about what is going on with all four examples in Pattern One. They might do so individually at first then work in a small team to refine their ideas and the way they express those ideas.

Expect ideas like:

• If the denominators of the fractions are the same, and the numerators add to the denominator, the sum is one.
• If the two numerators add to the denominator, then the sum is one.

Your aim is for students to express their claims in clear, minimal terms, using correct mathematical language. For example, ‘the top numbers’ is not as clear as ‘the numerators’, and ‘add to’ is not as precise as ‘the sum of’.

Representation

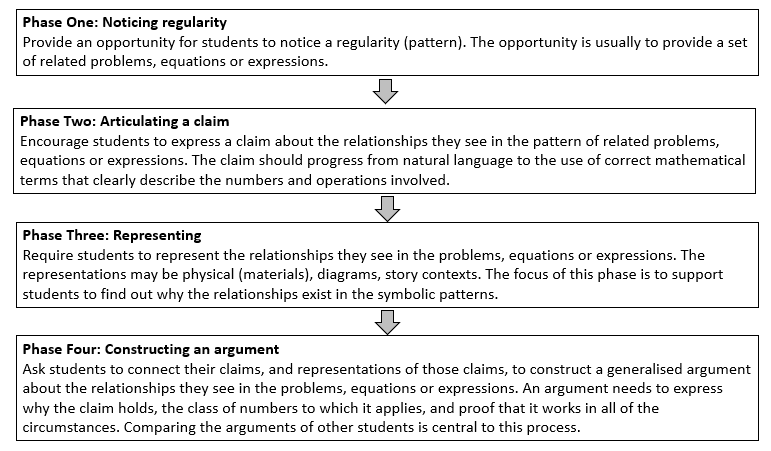
In this phase, students choose representations to show why the pattern holds consistently. Students might choose physical manipulatives, such as fraction strips or circles, draw diagrams such as strips and circles, and use contexts from everyday life, such as sharing cakes or pizza. Encourage students to begin with the first two examples of equations then consider how the same relationships might generalise to the last, and other similar, equation pairs.

Examples might be:

• I made 1/2 + 1/2 = 1 using fraction strips then I made 1/5 + 4/5 = 5/5 . Five fifths make one, so I put a one strip below.
   
• S: I used fraction circles to show that 1/8 + 7/8 = 1 and 1/3 + 2/3 = 1.
  

Some representations are less helpful than others in terms of understanding the structure of the fractions that add to one. Circles are useful for showing that one is complete. Strips may make the iteration of unit fractions more obvious. Strips are also easier for students to draw, and divide up equally. Ensure your students have experience with a mix of circle and strip fraction models. It is important for students to recognise that the denominator in each example defines the size of the equal parts that one is cut into. For example, eighths are created by the equi-partitioning of one into eight parts, so eight of those parts make one. Your questioning is important to support students to connect the symbols and other representations.

• Explain where the eighths are in your representation.
• How many eighths are needed to make one?
• Where is the seven, in 7/8 represented in your diagram/model?
• How does your representation show that the sum is always one?

Argumentation

In this phase students are asked to formalise their noticing by creating a statement that generalises to all cases. The discussion may start with a specific equation pair but must be amended so that it accurately represents the general pattern.

S: With 1/8 + 7/8 = 1 the numerators add to eight. Eight eighths equal one.

T: So how does that work in the same way with the other equations?

This might lead to expressing the relationship in general terms.

S: The first numerator plus the second numerator add up to the denominator.

T: If we gave names to the numerator and denominator of the first fraction, like a and b, could we express the property more simply?

Some students might experiment with algebraic notation such as a/b + c/b = 1. Note that this statement is incomplete since it misses the necessary condition for a + c = b.

T: Do we need to say something about a and c?

S: We could just write a + c = b.

T: Give us an example of that.

S: If b = 3, the numerators 1 and 2 add to 3.

Though it is difficult for this level, increased sophistication is evident in a + c = b, and writing the generalisation with only two variables, a/b+ (b-1)/b = 1. It is also important to note that b/b = 1, for any whole number value of b, except zero. b can also be any integer, since rational numbers are of the form a/b, a and b∈ I, that is a and b must be integers. High achievers should be challenged to express their generalisations using algebra. You may need to support them to develop the coding strategies to do that.

Equation Pairs Set Two

If time permits in the first lesson, ask the students to approach the second equation set more independently. From this point each equation set is discussed succinctly using the phases of the approach.

Noticing consistency

The four equations apply the addition of fractions with the same denominator. Students need to recognise that the denominators in both addends and the in sum are the same. Watch for students incorrectly applying whole number addition, that is, adding both numerators together and adding both denominators together. The completed equations should be:

Note that ten eighths equals 1  2/8 = 1  1/4

Making a claim

In natural language expect the students to use phrases like “you just add the top numbers”. Introduce important vocabulary such as numerator, denominator, addend, and sum to clarify which numbers are being referred to in the claims. If the claim is restricted to one example, encourage students to see what changes and what stays constant across the other three equations. The aim is to broaden the claim to the equivalent of “If the denominator of both addends is the same, then the numerator of the sum is the sum of the numerators of the addends.”

Representation

Expect both physical and diagrammatic representations to be used. A fraction strip representation might look like this:

Diagrams of a ‘sets’ representation can be used but it is unwise to use sets at this point (See the diagram below). The changing whole can be confusing, since the aim is to generalise a relationship for all examples.

Whatever representation is chosen by students they need to be clear about the referent one, be it a length, area, or set. The sum must be defined in terms of that original one whole.

Argumentation

Look for students to justify that if the denominators of two addends are the same then the sum is the sum of the numerators, over that denominator. Algebraically that is represented as:

a/b + c/b = (a+c)/b

Note that a, b, and c are variables, and the generalised argument becomes clearer, and is confirmed, by translating values from the equations back into the general form.

For example, with 3/8 + 7/8 = 10/8, a = 3, b = 8, and c = 7.

An interesting discussion point is whether this is any different to addition of whole numbers. For example, 3 + 7 = 10 is the combining of 3 ones and 7 ones, making 10 ones. The ‘ones’ are regarded as the same unit. With 3/8 + 7/8 = 10/8, eighths are the units being combined.

Developing the process further

PowerPoint One contains seven equation sets. The sets might form the basis of a week-long unit. The phases for each equation set are described succinctly below.

Equations Set Three

Noticing consistency

The four equations both demonstrate the multiplication of unit fractions, that is fractions with one as the numerator. Understanding in general that 1/b × 1/d = 1/bd, e.g. 1/3 × 1/4 = 1/12, is fundamental for understanding equivalent fractions.

Making a claim

In natural language, expect the students to use phrases like “multiply the two denominators and you get the denominator of the answer”. Expect the use of mathematical vocabulary such as factor and product to clarify which numbers are being referred to in the claims. Encourage clarity by asking questions like:

• Do the denominators of the factors need to be the same?
• What can you say about the numerators?

The aim is to state the claim as something like “The product of two unit-fractions is a unit fraction, with a denominator that is the product of the denominators.”

Representation

Expect both physical and diagrammatic representations to be used. Fraction strips are static representations:

Folding a paper strip or a rectangle is a dynamic representation:

A sets model may be used but the product needs to be known to establish the possible numbers of objects in the set. Therefore, identifying the referent one is more complex.

Argumentation

Look for students to state the condition that both addends are unit fractions. The starting product might be expressed as 1/b × 1/d. The product is 1/bd. Students should explain why the relationship occurs. Their explanation needs not be in formal algebraic terms, with letters as variables.

The second factor gives the first equal partitioning and creates some parts. The denominator gives the number of equal parts. Then each part is split into equal parts. That number of parts is given by the denominator of the first factor. Therefore, each of the d parts, is equally partitioned into b parts, so the total number of parts equals b x d.

Equation Pairs Set Four

Noticing consistency

The four equations apply equivalence of improper fractions. The equivalent number is kept at three to limit variation.

Making a claim

In natural language expect the students to use phrases like “the answer is always three.” Some students might indicate what they see in a diagram.

Expect the use of mathematical vocabulary such as denominator, numerator, fraction, equivalent, and whole number to clarify which numbers are being referred to in the claims. Encourage clarity by asking questions like:

• What does the equals sign indicate? (both numbers represent the same amount)
• How is the numerator related to the denominator? (the numerator is the denominator multiplied by three)
• Why is the number on the right side always three? (For example, with 24 eighths you can make three ones because you need eight eighths to make each one.)

The aim is to state the claim as something like “A fraction that has a denominator that divides into the numerator three times, is equal to three,” or “A fraction that has a numerator that is three times the denominator, is equal to three,”

Representation

Fraction circles are useful in demonstrating the completeness of a one.

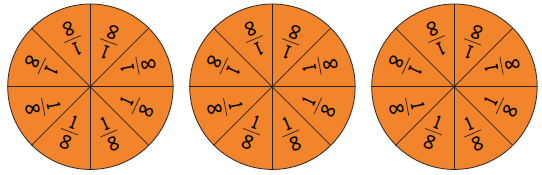
Eight eighths make one. With 24 eighths you can make 24 ÷ 8 = 3 ones.

Students may develop more schematic ways to represent the connection between numerator and denominator.

Five fifths make one so 15 fifths must make three, since 3 x 5 =15

Argumentation

Look for students to justify, using words of diagrams, that the denominator of a fraction specifies the number of equal parts that make one. For example, in 12/4 the parts are quarters, four of them are needed to make one. Dividing the numerator by the denominator finds how many ones can be made. With 12/4, 12 ÷ 4 = 3, so three ones can be made. The equation 12/4=3 represents that equivalence.

For all four equations define the denominator of the first fraction as the variable, say b. The observation that the numerator is always the denominator multiplied by three can be represented as 3b/b. The equivalence can be written as 3b/b=3.

Arguments may be supported by graphics or other representations.

Students might also generalise that dividing the numerator by the denominator tells how many ones can be made, and the remainder becomes the fraction part of the mixed number, e.g. 13/5 = 2 3/5.

Equation Pairs Set Five

Noticing consistency

The equation set applies equivalence, that is when two fractions represent the same value. Understanding equivalence is essential to ordering fractions by size and to the addition and subtraction of fractions. The completed sets should be:

Making a claim

In natural language expect the students to use phrases like “If the numerator is three times the other numerator, then the denominator must be three times as well.” Students tend to notice patterns across the equation like this:

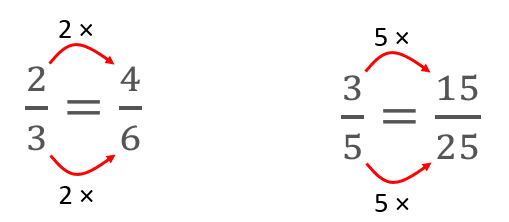
Expect the use of mathematical vocabulary associated with fractions, particularly numerator and denominator. Draw students’ attention to the equals sign as representing the same value on both sides. Students are most likely to see equals as a signal to work out the answer.  Encourage clarity by asking questions like:

• What is the same about all four equations?
• What is different?
• How are the numerators related?
• How are the denominators related?

The aim is to state the claim as something like “Two fractions are equivalent, if the one numerator is a multiple of the other, and the denominator is the same multiple of the other.”

Representation

Static representations might involve length, area (circles or rectangles), or sets.

A more dynamic representation is to fold a paper strip or rectangle into thirds, shade two thirds, then fold the thirds in half. How many sixths are shaded?

Argumentation

Look for students to justify, using words of diagrams, that the same multiplication is performed on both the numerator and denominator of a fraction to create an equivalent (same value) fraction. For example, if the numerator and denominator of 2/3 are multiplied by six this gives 12/18, and 2/3 = 12/18. Of interest is that the multiplier 6/6 is another name for one, the identity element for multiplication. 2/3 x 6/6 = 12/18 is the same operation as 2/3 x 1 = 12/18.

However, the multiplication means different things for the numerator and denominator. Multiplying the numerator by a number increases the number of parts by that factor. For example, 12/18 has six times as many parts as 2/3. For the denominator the effect is the inverse. Each part in the new fraction is one sixth that of the first fraction, since six times as many of those parts make one. For example, 12/18 has parts that are one sixth the size of the parts in 2/3.

In general, the transformation a/b × n/n = an/bn, gives n times as many parts but each part is one nth the size. a/b  and an/bn represent the same quantity. Note that n/n is always equal to one.

Equation Pairs Set Six

Noticing consistency

The equation set highlights the difference of unit fractions. Note that the denominator of the first fraction is one less than that of the second. This equation set provides an opportunity to apply equivalence. The completed sets should be:

Making a claim

In natural language expect the students to use phrases like “the difference has a denominator that is the product of the two other denominators.” Ask students to be more specific in their description.

• What can you say about the two fractions on the left of each equation? (They are both unit fractions and there is a difference of one in their denominators)
• What does subtraction mean in these equations? (It means "What is the difference between the two fractions? ")
• Can you make up another equation that would go in this set?

The aim is to state the claim as something like “If two unit-fractions have denominators that are one different, the difference of the fractions is the unit fraction with the product of the denominators as its denominator.”

Representation

Students are likely to use specific examples to convince others about how the relationships work. Fraction strips are probably the most useful representation.

It is important for students to consider why the fraction one twelfth fits exactly.

Argumentation

Students need to apply equivalence to argue why a given unit fraction is the difference. Their argument might begin for a specific example.

Since one half and one third are involved, the difference must involve sixths, as both one half and one third can be renamed as ‘so many’ sixths. 1/2 = 3/6 and 1/3 = 2/6 so there is a difference of one sixth.

Encourage the students to generalise by naming the denominator of the first fraction as a variable again.

• Can you find a relationship that applies to all four equations?

If the first fraction is 1/b, the second is 1/(b+1),  and the product is 1/(b(b+1)). Algebraic notation, like this, is not expected at Level Four, but students may invent their own ways to express what they notice. Whatever notation students create, it can be checked by substituting numbers in place of symbols, and seeing if the equations created belong in the set. This could be done as a paired activity, and could be used to encourage tuakana-teina.

Equation Pairs Set Seven

Use set seven as an opportunity to see how well students engage in the generalisation process independently. Ask them to record their claims, representations, and arguments in ways that work for them. Some students may prefer writing their work while others may prefer to capture their ideas using a digital recording.

Noticing consistency

The equation set highlights the multiplication of fractions, that is a fraction of a fraction. The numerators of the factors are the same, as are the denominators. That is done to reduce variation. The completed sets should be:

Making a claim

In natural language expect the students to use phrases like “It is a fraction multiplied by itself. The product is the two numerators multiplied over the two denominators multiplied.” Ask students to be more specific in their description, through questions like:

• What do you notice about the two factors (fractions being multiplied)? (they are the same)
• Do you know a mathematical term for a number multiplied by itself? (square of the number)
• Can you use the term square to describe the product fraction in a simpler way?

The claim, using mathematical language, might be something like, “If a fraction is squared, the product is the numerator squared over the denominator squared.”

Representation

An area model is useful since it illustrates the relationship between a number multiplied by itself and a square. Folding and shading squares of paper works well.

Students might also use strip models, but the squaring of numerators and denominators is not obvious.

Argumentation

The equations include two variables, that is the value of numerator and denominator in the fraction being squared. Students need to recognise that the denominator names the number of partitions of one. The numerator names the count of those parts.

Students may be able to show how they are thinking with variables (lack of closure), by treating the numerator and denominator as variables in an area diagram.

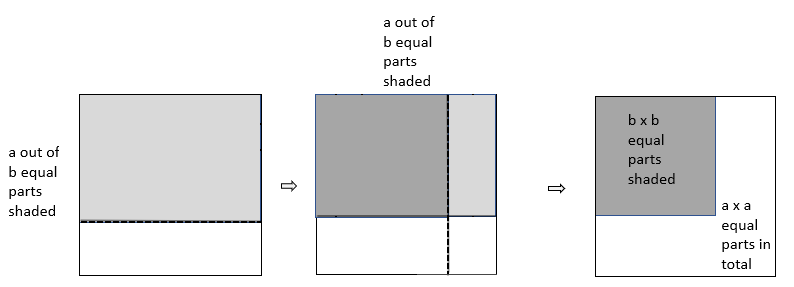
Algebraically this might be written as a/b × a/b = (a×a)/(b×b) or more succinctly as (a/b)² = a²/b².