These are level 3 number and statistics problems and level 4 algebra problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (416 KB)
use addition and subtraction facts to solve problems (Problem 1)
find patterns in multiplication equations (Problem 2)
find outcomes using diagrams (Problem 3)
use addition and mutliplication to solve problems (Problem 4)
Problem One
a. 6 = 9 + 2 – 5. With the plus meaning “putting together” and the minus meaning “taking away”, you can get variations of the first diagram shown in the Answers.
Encourage the students to think about the lengths of the other dimensions of Cuisenaire rods. They’ll probably know that they are 1 centimetre wide. So they can also make 6 by putting either the 2 or the 9 sideways against the 5.
b. The answers allow for using the width (1 centimetre) of any of the rods.
Challenge the students to try to make all the lengths from 1 to 16 centimetres without using the width of the Cuisenaire rods. You may need to remind them of the rules below to make their working more efficient:
odd + odd = even odd – odd = even
even + even = even even – even = even
odd + even = odd odd – even = odd or even – odd = odd
For example, if they are trying to make 8:
Combining even and odd lengths (2 + 5 or 2 + 9) will give an odd length. Combining 5 and 9 gives only 4 or 14. So 8 cannot be made by combining two of the rods. The possible combinations of three rods are (9 + 5) – 2, 9 + (5 – 2), (9 – 5) + 2, 9 – (5 + 2), 9 + 5 + 2, or (9 – 5) – 2, none of which give 8, so 8 cannot be made from 2, 5, and 9.
Working systematically in this way, the students will find that they can’t make 10, 13, or 15 either.
Extension
Give the students a different combination of three Cuisenaire rods to make into various lengths.
Problem Two
The students will probably see the patterns in this set of equations fairly quickly. The left-side factors are multiples of 3, and the digit that is repeated six times in the product increases by one for each successive equation.
From these observations, they will be able to answer question a: 333 333 and 444 444.
To answer question b, they might just continue the pattern and write out the equations until they get to the product 777 777. But they can solve the problem far more efficiently if they look for a relationship between the left-side factors and the products.
The digit that is repeated six times in the product is the left-side factor divided by 3, or conversely, multiply the digit repeated six times in the product by 3 to get the factor. For example, 7 x 3 = 21, so 21 x 37 037 = 777 777.
Another way of approaching this problem is to look at the relationship between the first equation and successive equations:
3 x 37 037 = 111 111
9 x 37 037 is 3 x (3 x 37 037), so 9 x 37 037 is 3 x 111 111 = 333 333.
x 37 037 = 777 777, so must be 7 x 3, or 21.
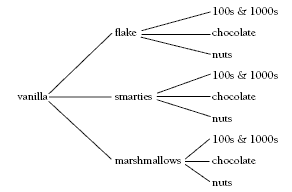
Problem Three
The students should be able to confidently use a tree diagram to solve this problem. The vanilla ice cream section should look like this:
After the students have drawn a tree diagram, discuss with them more efficient ways of solving the problem. Is there any way they could calculate the answer without having to draw a diagram?
Using the tree diagram to illustrate your points, explain that there are three flavours of ice cream. Next, they have three choices of confectionery. Altogether, this is three lots of three choices, or 3 x 3 = 9 different types of ice cream and confectionery. Finally, they have another three choices of topping, which is 9 x 3 = 27 different types of ice cream with confectionery and topping.
Students working at level 4 will be starting to use exponents and should see that 3 x 3 x 3 is the same as 33.
number of choices →3 ← number of items put on each ice cream cone
Give them several different examples so that they understand which number is the base number and which is the exponent. For example, there are four flavours of ice cream and four toppings. How is this written using an exponent? (42) There are two flavours of ice cream, two types of confectionery, and two toppings. How is this written using exponents? (23)There are only five flavours of ice cream and no confectionery or topping. How is this written? (51.)
Extension
Ask the students to make up a problem of this type with 64 as the answer (64 is 43, 26, or 82).
Problem Four
This can be calculated by noting how many Saturday, Sunday, and weekday papers there are and how much each of these three types of paper costs. The students need to know that September has 30 days. If they don’t know this, they could look at a calendar or recall the rhyme that tells the lengths of all the months.
If 3 September is a Saturday, then so is September 10, 17, and 24. This means four Saturday papers, and they cost 4 x 90 = 360 cents or $3.60.
Similarly, there are four Sunday papers, and they cost 4 x $1.50 = $6.00.
So you have 30 – 4 – 4 = 22 weekdays. Papers on these days will cost
22 x 80 = 1 760 = $17.60.
The total cost of papers is therefore $3.60 + $6.00 + $17.60 = $27.20.
Hints for Students
1. a. This is really about numbers. How can you get 6 using 2, 5, and 9?
Or is there some other piece of information that you know about Cuisenaire rods that
might be useful?
b. What is the longest possible length? Can you make all the lengths 1, 2, 3, and
so on up to that length? Why? Why not? You might not need all three rods.
2. Look for the pattern in the left-side factors (3, 6, 9, 12, …) and the pattern in the products (111 111, 222 222, …).
Can you see a connection between the left-side factors and the products?
3. Work systematically. A tree diagram could help.
4. Look for a systematic way to calculate the total.
Answers to Problems
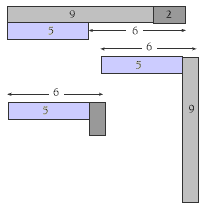
1. a. Some possible ways are:
b. If you include the 1 cm width of the rods, you can get all the other lengths between 1 and 16:
1 cm (using the width of a rod), 2 cm,
3 cm (5 – 2 or 2 + the width of a rod),
4 cm (9 – 5 or 5 – the width of a rod),
5 cm, 7 cm (5 + 2), 8 cm (5 + 2 + the width of the 9 rod), 9 cm, 10 cm (9 + the width of a rod), 11 cm (9 + 2), 12 cm (9 + 5 – 2), 13 cm (9 + 5 – the width of the 2 rod), 14 cm (9 + 5), 15 cm (9 + 5 + the width of the 2 rod), and 16 cm (9 + 5 + 2).
2. a. iii. 333 333
iv. 444 444
b. 21
c. You may notice that the left side factors are multiples of 3. The digit that is repeated six times in the product is the left-side factor divided by 3.
3. 27
4. $27.20