The purpose of this unit is to build upon the knowledge students have of combining and separating groupings to five and to use this as a building block to knowing combinations within and up to ten.
- Instantly recognise and describe a group of five in multiple representations of numbers within and to ten.
- Apply and record the operation of addition for groupings within ten.
- Understand the language of subtraction and apply the operation of subtraction to groupings within ten.
- Make connections between the operations of addition and subtraction and develop and understanding of the relationships underpinning the family of facts.
- Know and apply addition and subtraction facts within ten.
The ability of young children to recognise small quantities without counting has been somewhat overlooked in the early emphasis we have given to counting. These lessons build upon the student’s recognition and knowledge of groupings to five, to scaffold ready combinations and separations in numbers to ten.
A goal within primary mathematics is for students to use partitioning strategies when operating on numbers. By building images and knowledge of basic combinations at an early age, the ability to naturally partition larger numbers will be strengthened. Students should be encouraged to instantly recognise and use their knowledge of these combinations rather than relying for an unduly prolonged period on counting strategies.
This set of lessons focuses on knowing combinations of numbers between five and ten. They develop the quinary (fives) partitioning of ‘five and’, whilst consolidating combinations (+) and separations (-) within five.
A range of equipment is available to represent these quinary partitions. Students should be encouraged to make the connections between each of these representations as well as creating some of their own.
In communicating mathematical ideas, students learn to understand and use relevant language, symbols, text and diagrams to express their thinking and record concepts in a range of contexts and in a variety of ways. Teachers have a key role in developing the students’ ability to communicate their mathematical understandings orally and in writing.
The activities suggested in this series of lessons can form the basis of independent practice tasks.
It is important to note that the focus of this unit is on instantly recognising (subitising) collections and not on counting the collection. While many students may be able to count a set of objects they may not be as proficient at subitising small collections. Ways to support students include:
- providing multiple opportunities to subitise with smaller collections up to five before moving onto larger groups
- varying the arrangements of the objects (e.g.in a line, in a dice pattern, closely grouped, randomly spread) and the objects (counters, toys, pencils, pebbles).
This unit is focussed on combining and separating groupings to five. This should be used as a building block to knowing combinations within and up to ten. As a result of this focus, the learning in this unit is not set in a real world context. The context for this unit can be adapted to suit the interests and experiences of your students
- by using collections that are part of the classroom or school environment (e.g. blocks, counters, plastic animals, pens, pebbles, leaves, seeds)
- using te reo Māori for numbers tahi to tekau (one to ten) and counting.
- Tens frames
- Number Strips
- Transparent counters
- Animal strips
- 20 beads frame
- Finger patterns
- Dice
- Playing cards
- Murtles 5 and ... (Material Master 5-9)
- Numeral cards
- Copymaster 1
- Copymaster 2
- Copymaster 3
Session 1
SLO: To recognise and describe a group of five in multiple representations of numbers within and to ten.
Activity 1
- Make paper, crayons/felts, pencils, counters (or similar mathematics equipment) available to the students. Set a time limit as appropriate. Have the students write, draw and show you everything they know about five. This, and the next step, could be done in pairs to encourage tuakana-teina.
- Have the students pair share their work.
- Write the words ‘five’ and rima, and the numeral '5' on a paper chart, whiteboard, or in a modeling book. Collect and record the important ideas that the students have generated. Be sure to use words, symbols and drawings of equations, stories or materials.
Activity 2
- Show tens frame for 5.
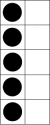
Describe it in words: ‘There are five dots filling up one column (or side) of the tens frame’. Or, ‘There are five dots. They fill up half of the tens frame'. Or, ‘There are five dots filling one side of the tens frame and five empty spaces on the other.’ Have the students describe to a partner what they see. Hide the tens frame. Have the student repeat their description to their partner of what they see in their mind.
- Show the tens frames for 6, 7, 8, 9, 10.
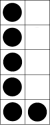




For each say the number of dots and repeat 1 above. Encourage participation and accuracy in the oral descriptions including saying how many empty spaces. For example: ‘Seven. Five dots and two dots and there are three empty spaces.’
- Show the tens frames in random order and have the students say the number, make it on their fingers and show a partner.
- Include all tens frames and repeat above, this time with say, show, and write (make writing materials available, or have them use a ‘magic finger’ to write on the surface in front of them or in the air.)







Activity 3
- Introduce a 20 beads frame and animal strips. Discuss the similarities of the representations, model descriptions then have the students describe what they see.
For example: ‘Seven. There are five white beads and two red ones.’
For example: ‘Seven. There are five dolphins and two more dolphins after the dotted line.’
Repeat with the beads or animal strips hidden. Have the students describe a number image to a partner, then show it to them to check to see if they are correct.
- Distribute writing materials. Show numeral cards to 10 in random order and have them draw a matching image (using dots or beads). Emphasise the need for their drawing to show a group of five for numbers 6 – 10. Display the students’ work.
Session 2
SLO: To apply and record the operation of addition for groupings within ten.
Activity 1
- Show the children a dice. Discuss, record and read the dot combinations for four.
4 = 2 + 2, ‘Four is the same as two and two.’
1 + 3 = 4 , ‘One plus three equals four.’
- Show the students other dice faces and have them write and share equations for these. Encourage students to record equations both ways as above. Use the language ‘equals’ and ‘is the same as’.
- Hide the dice, say one of the numbers and ask the students to draw it. Repeat.
Activity 2
- Repeat Activity 1 above with tens frames cards 5 – 10.
- Have the students work in pairs to play Scoring a Tri. (Purpose: to quickly recognise representations of the numbers 5 – 10).
Make the link for the students between tri and three, for example: tricycle (3 wheels), triangle (3 sides and corners).
Each pair has three shuffled piles of cards turned upside down between them:- pile 1: tens frames 5 - 10
- pile 2: digit cards 5 – 10
- pile 3: equation cards 5 + 1 to 5 + 5 (Copymaster 1).
Compete to see who can ‘score a tri’ by turning over 3 matching cards. For example: 
- Students can repeat the game using animal strips, number word cards (instead of digit cards) and expressions. The winner is the person with the most sets.
Activity 3
- Show an 8 tens frame. Pose the question “Is 5 + 3 the only way of writing something that is the same as 8?” Discuss and chart the multiple combinations that are the same as 8.
- Distribute a tens frame (5 – 9) to each student and have them each write different combinations for the number of dots depicted.
- Have each student share with a partner what they have done and ask, ‘Have I got them all?’
- Conclude by revisiting the quinary (fives based) equipment used so far and reminding the students of how useful “5 and” is.
Activity 4
Play Murtles 5 and... (MM 5-9) (Purpose: to practice and know 5 + addition facts to 9)
Session 3
SLO: To understand the language of subtraction and apply the operation of subtraction to groupings within ten.
Activity 1
- Tell and write with the students a subtraction story about someone in the class. For example: Erika was sharing her carrot sticks with Sadie. She had eight and gave three to Sadie. How many did Erika have for herself? Ask the students to record what happened using numbers and have them share their recording.
- Model 8 – 3 = 5 on chart paper or in a modelling book (to keep and refer to later). Draw a box around 8 and highlight this is what Erika started with. Talk about how many she gave away and how many were left. Brainstorm and record words for the – subtraction sign. These should include ‘give away, take away, subtract, minus, less’. Read 8 – 3 = 5 several times using all of the words. Emphasise that they mean the same thing.
- Explain that 8 – 3 = 5 is known as an equation because it has the equals sign which means that 8 - 3 is the same as 5. Make the link between the word equals and the word equation.
- Ask the students which is the biggest number in the equation. Ask them why it comes first. Have them model with equipment to understand that you can’t subtract a smaller number from a bigger number (we are not discussing negative numbers here)
- Record the important points discussed on the chart paper.
Activity 2
- Distribute a card with a subtraction expression (Copymaster 2) to each student. Have them make a silent decision whether or not the result of the subtraction will be 5. Have them form two groups, a ‘Yes’ group and a ‘No’ group.
- Have them take turns modelling their equation on the 20 beads (with 10 of the beads covered as they are not needed here) to show and explain why they are correct.
- Ask the students whether knowing about the tens frames helped. With reference to the 20 beads frame, model the connection between 5 + 3 = 8 and 8 – 3 = 5.
- In Attachment 1 there are three expressions, 5 – 7, 5 – 8, and 5 – 9 that are included to provoke discussion about why the big number comes first in subtraction equations. Refer to the chart made in 1 above to emphasise this point.
Activity 3
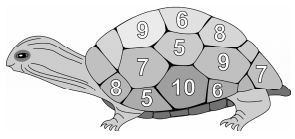
Have the students work in pairs to play Murtles 5 and... (MM 5-9) in reverse. (Purpose: to practice and know subtraction facts that make 5).
Each student covers all the numbers with see-through counters. They take turns to roll the dice.
If the number rolled can be subtracted from a covered number to leave a result of five, the counter can be removed. The aim of the game is to be the first to lighten Murtle Turtle’s load by clearing all the counters.


Session 4
SLO: To make connections between the operations of addition and subtraction and develop an understanding of the relationships underpinning the family of facts.
Activity 1
- With reference to the 20 beads frame, model the connection between 5 + 3 = 8 and 8 – 3 = 5. Talk about and record these equations and what the students notice about them, in particular that they have the same three numbers. Emphasise that these numbers have a special relationship and that this relationship sometimes means that we talk about “families” of numbers that are related.
- With the group (or class) place a number strip where all the students can see it. Ask what they notice about it (That it is coloured in groups of five). Connect this to the other quinary materials you have been using.
- Have students model with see-through counters on the number strip and record 5 + 3 = 8 and 8 – 3 = 5. Ask if there is something else they can see with these numbers. Encourage them to see: 3 + 5 = 8 and 8 – 5 = 3. Together, model and record all four equations using another number up to 10. Model the same equation on a tens frame. Discuss what is the same about the representations. Emphasise the inverse relationship between addition and subtraction and the phrase : ‘If I know this (eg. 5 + 3 = 8) then I know this (eg. 8 – 3 = 5).’
- Explain the class is making a display of ‘number families’, sometimes called ‘families of facts’. Ask, ‘What is a fact?’ Emphasise that a fact is a true statement.
- Distribute number strips, blank tens frames and counters to pairs of students. Have them make, draw and record in pairs ‘families of facts’ associated with some of the numbers 5 – 10. They can choose to use number strips, tens frames or both. Encourage the students to record the families of different combinations, not just those of ‘5 and’ such as 5 + 3 = 8 (5 + 3 = 8, 3 + 5 = 8, 8 – 5 = 3, 8 – 3 = 5) but also 6 + 2 = 8 (6 + 2 = 8, 2 + 6 = 8, 8 – 2 = 6, 8 – 6 = 2).
- Discuss and display the students’ work.
Activity 2
Have the students in pairs play ‘Go Fish’ or ‘Happy Families’ Copymaster 3 (Purpose: to identify all members of families of facts)
5 + 4 = 9 4 + 5 = 9 9 – 5 = 4 9 – 4 = 5
The aim of the game is to make the greatest number of complete families of facts. To play:
- The Family of Fact cards are shuffled and placed face down. Each player takes seven cards.
- The players sort their cards in their hand into ‘families’, identifying complete families and placing these face up in front of them.
- Each player takes turns to ask their partner for missing family members. If their partner cannot supply the card, they are told to ‘Go fish’. They take a card from the pile.
The game is played till all the cards are used and the winner is the person with the most complete families.
Session 5
SLO : To know and apply addition and subtraction facts within ten.
- Show selected tens frames, 20 beads frame and animal strips modelling example equations such as "7 and 2". Have students model these with their fingers and talk about the related addition and subtraction equations.
- Explain that they will be playing some games just working with numbers, but that they might like to picture fingers, tens frames, bead frames or animals to help them if they need to.
- Explain the purpose of the activities is to practice what they know.
- In pairs play the following games, using playing cards with Kings, Jacks and tens removed, and using the Queen as a zero:
‘Snap’ for a chosen number to 9 (Purpose: to practice and know addition and subtraction facts to 9):
Students draw a number from the pile, for example 7. This becomes the chosen number they must make.
One card is turned over to begin the game.
Students take turns to turn over a card from the pack, placing the turned card on top of the card before. If the turned card can combine in some way with the previous card to make the chosen number, the student says ‘Snap’, states the equation and collects the pile of cards.
The game begins again with the same chosen number.
For example, for the chosen number 7: if 9 is turned, followed by a 2, 9 – 2 = 7 is stated and the pile of cards is collected, or if 3 is turned, followed by 4, 3 + 4 = 7 is stated and the pile is collected.
‘Memory’ for a chosen number to 9 (Purpose: to practice and know addition and subtraction facts to 9):
Cards are turned down and spread out in front of the students. A chosen number is turned over and identified.
Students take turns to draw pairs. If the cards can make the chosen number, using either addition or subtraction, the pair is kept by the player. For example: 4 is turned over and identified as the chosen card. A player draws a 6 and a 2, and states 6 – 2 = 4 and keeps the pair, or a player draws 1 and 3 and states 1 + 3 = 4 and keeps the pair.
The game continues until all cards are used up.
The winner is the person with the most pairs.
‘Dice pairs’ for a chosen number to 9 (Purpose: to practice and know addition and subtraction facts to 9 and family of facts members):
Each player has a blank tens frame and ten counters to place one at a time on the frame to record their score. The winner is the first one to fill their frame.
Players roll two dice, combine these to identify a chosen number of 9 or less. If the combination is more than 9 they roll again.
Players take turns to roll the two dice to make the identified number. Each time they are successful and can state an equation and the other 3 members of the family of facts, they score by placing one counter on their tens frame. For example: If 8 is the chosen number. A player rolls a 2 and a 6 and states 6 + 2 = 8, 2 + 6 = 8, 8 – 2 = 6, 8 – 6 = 2. They are correct and place one counter on their tens frame.
Have students each make puzzle cards for the class to use. (Purpose: to depict a context for a family of facts and record these):
Make available cards marked in 3 sections as shown below, felts/crayons and scissors. Have the students draw pictures of equations, write them, then cut into two puzzle pieces to match. When several have been created, students can play memory match, by turning the pieces upside down and trying to find pictures and matching equations.
Dear parents and whānau,
In class we have been practising addition and subtraction facts up to 9. Ask your child to show you some on their fingers or draw some tens frame pictures to show you what they have been learning. We have been playing these games with cards and dice in class.
Have your child explain how to play these games. They should be fun to play! Use playing cards with Kings, Jacks and tens removed, and using the Queen as a zero.
‘Snap’ for a chosen number to 9.
A player draws a number from the pile, for example 7.
This becomes the chosen number they must make.
One card is turned over to begin the game.
Players take turns to turn over a card from the pack, placing the turned card on top of the card before. If the turned card can combine in some way with the previous card to make the chosen number, the player says ‘Snap’, states the equation and collects the pile of cards.
The game begins again with the same chosen number.
For example: if 9 is turned, followed by a 2, 9 – 2 = 7 is stated and the pile of cards is collected, or if 3 is turned, followed by 4, 3 + 4 = 7 is stated and the pile is collected.
‘Memory’ for a chosen number to 9.
Cards are turned down and spread out in front of the players.
A chosen number is turned over and identified.
Players take turns to draw pairs.
If the cards can make the chosen number, using either addition or subtraction, the pair is kept by the player.
For example: 4 is turned over and identified as the chosen card. A player draws a 6 and a 2, and states 6 – 2 = 4 and keeps the pair, or a player draws 1 and 3 and states 1 + 3 = 4 and keeps the pair.
The game continues till all cards are used up.
The winner is the person with the most pairs.

