This problem solving activity has a logic and reasoning focus.
Hannah has a square crate that can hold nine cartons of milk.
In how many ways can she put three cartons of strawberry milk in the crate so that they form a line?
- Rotate pattern pieces through quarter and half turns.
- Be systematic and count possibilities.
This problem develops two concepts. The first is counting all possible arrangements, and the second is noticing that some of these arrangements are ‘alike', and so might be considered to be the same.
The first part of this problem has students following these steps:
- find some answers to a problem;
- think about whether there are any more answers or not;
- try to explain why there are no more answers.
The students should be encouraged to try to find a number of answers and to reach a point where they have some systematic idea as to why there are no more answers. There are three important skills that are fundamental to all of mathematics; being able to find some possibilities, getting all possibilities, and justifying that there are no more possibilities. We work through this sequence in the Solution.
The second idea in this problem is symmetry. This involves noticing that turning some arrangements of the milk cartons through quarter turns will give another arrangement. The two arrangements are said to be ‘alike'. The aim is to find such alike arrangements, put them into groups, and calculate how many alike groups there are. This will confirm the number of different arrangements, or the number of groups that are not ‘alike'. To do this, students should have some knowledge of what is meant by a quarter turn.
The basis for two arrangements being alike is discussed in the Level 1 logic and reasoning problem Strawberry Milk.
- Copymaster of the problem (Māori)
- Copymaster of the problem (English)
- Copymaster of 4 by 4 crates
- Copymaster of 3 by 3 crates
- Bottles tops
- Coloured pens and paper
The Problem
Hannah has a square crate that can hold nine cartons of milk. In how many ways can she put three cartons of strawberry milk in the crate so that they form a line?
.gif)
Teaching Sequence
- Show the children a 3 x 3 grid and tell the class Hannah’s problem. Ask:
What might you need to help you solve the problem? How will you record what you find out? - Distribute the bottle tops and demonstrate how they can be used to form a line of milk bottles in a crate. Explain that the lines can be horizontal, vertical, or diagonal. Explain what is meant by 'alike' arrangements and a quarter turn.
As students work on the problem, ask questions that support them to explore all possibilities. Students could also experiment with a digital representation of the problem (e.g on Google Slides or Sheets).
How have your organised the milk bottles?
What possibility will you try next?
How could you alter your current arrangement to create a new arrangement?
How will you record each new arrangement? - As some solutions emerge, have several students present a picture of one of their arrangements. Title each with the relevant student's name.
- Ask all the students:
How do you know if there are any more?
How do you know if two answers are alike? - Encourage them to use a systematic approach to find all the possible arrangements (see the Solution).
- As appropriate, have students explore the Extension.
Extension
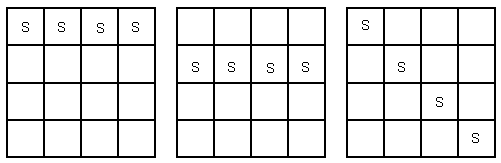
Hannah has another square milk crate. It can hold 16 bottles. In how many ways can she put four cartons of milk in her crate so that they form a line?

Solution
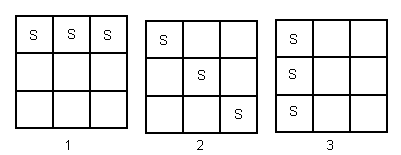
To be systematic, we need to look at where the end of the three in a line can be. Work round the crate starting at the top left-hand corner of the crate. This appears to give 3 answers. However, 1 and 3 are alike because a quarter turn of the crate will take 1 to 3. Therefore, we have two non-alike arrangements (see the Solution to the Level 1 Strawberry Milk problem.)
We also now know that we don’t have to think of any other arrangement that starts and ends with a corner square. This is because any such possibility would be alike with arrangements 1 and 2. Use the quarter turn test to demonstrate this.
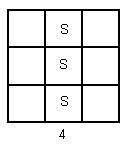
This now only leaves a line of three down the middle of the grid. Anything else can be turned into this, or one of the previous solutions, by a series of quarter turn(s).
So there are three different solutions, 1, 2, and 4.
Solution to the Extension
By going through the methods of Strawberry Milk and the Solution above, we get the following three possibilities.
You might like to think about what happens with 5 cartons in a line in a 5 by 5 crate. Is the answer 4?
Do you get the same answer for 6 cartons in a line in a 6 by 6 crate? What is the general pattern?