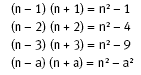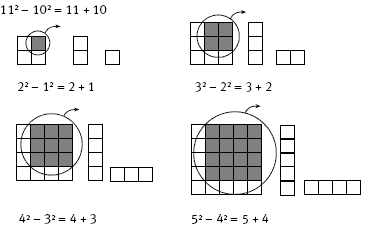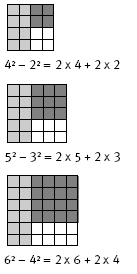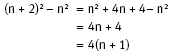This is a level 5 number activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (285 KB)
explore square number patterns
Multilink cubes or square grid paper
FIO, Level 4+, Number, Book Six, Squaring Off, pges 18-19
A classmate
This extensive but very interesting activity can help the students to develop strategies that will assist them with mental calculations. It may also give them a further sense of the fascination of numbers.
The particular number patterns that can be derived from this activity and that also provide powerful mental strategies are as follows:
1. The product of numbers that are equidistant from a middle number whose square is known can be calculated from this square number. To take some simple examples: 9 x 11 is the same as 102 – 12; 8 x 12 is the same as 102 – 22; 7 x 13 is the same as 102 – 32; and so on. This idea can be applied to much larger numbers, such as 26 x 34. This is the same as 302 – 42, which the students could work out in their heads as 900 – 16, which is 884. They could even tackle 47 x 53 mentally (that is,
502 – 32 = 2 500 – 9, which is 2 491) and 95 x 105 (1002 – 52 = 10 000 – 25, which is 9 975). The students are usually amazed at what they can accomplish mentally through using the power of patterns.
2. Finding the difference between adjacent square numbers can be done by simply adding the numbers. For example, 62 – 52 is the same as 6 + 5. Again, this pattern can be applied to relatively large numbers, such as 1002 – 992 (that is, 100 + 99 = 199) and 2 0252 – 2 0242 (that is 2 025 + 2 024 = 4 049).
3. If the difference between a pair of numbers is 2, then the difference between the squares of these two numbers is double the sum of the numbers. For example, 82 – 62 is the same as (2 x 8) + (2 x 6) or 2 x 14, which is 28. Likewise, 512 – 492 is the same as 2 x (51 + 49), which is 200.
4. The difference between pairs of squared numbers that are distant by 2 from each other can also be found by multiplying the intervening number by 4. In the examples above, 82 – 62 is the same as 4 x 7 (because 7 is between 8 and 6) and 512 – 492 is the same as 4 x 50 (because 50 is between 51 and 49).
The beauty about patterns such as those above is that some of the mental calculations they permit take less time than trying to do the original calculation on a calculator. In the last example, the calculator operation would involve squaring 49 and putting the product into memory, then squaring 51, and finally subtracting from it the recalled square of 49. It seems much easier to double the sum of 49 and 51 (which in this case is a very convenient doubling of 100) or to work out 4 x 50.
The activities and suggested mathematical models that allow the students to gain understanding of the patterns are set out in this activity in a nice developmental way. The answers for this activity provide additional possibilities for helping to facilitate such understanding.
Answers to Activity
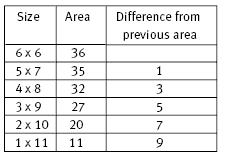
1. a. The horizontal sides are decreasing by 1 each time, and the vertical sides are increasing by 1 each time. The area also decreases each time.
bi.
ii. Answers may vary. The difference is going up in 2s, and the differences are
consecutive odd numbers.
c. The area of the initial square will vary, but the pattern of differences will be the same.
For example:
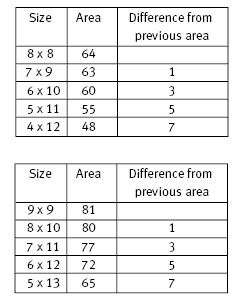
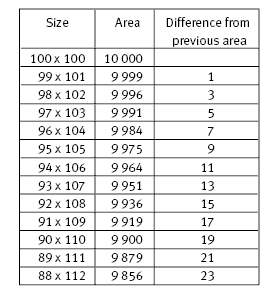
2 . a. A table of rectangles up to 88 x 112 should look
like this:
b. i. 9 996
ii. 9 964
iii. 9 856
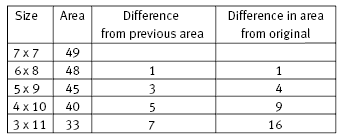
3. a. Yes, it will work with your other patterns.
For example:
b. As well as a table, there are various other ways, including:
•various algebraic formulae, for example: n x n = n2
4. a. Answers will vary. For example:
b.
c. i. 173
ii. 207
iii. 1 123
iv. 4 175
d. Explanations will vary. As shown in the diagrams for question 4a, if the total of the second squared number is removed, you are always left with the sum of the first number plus the second number.
5. a. Diagrams will vary. For example:
32 – 12 = 2 x 3 + 2 x 1 (where the 32 refers to the whole square, the 12 to the dark grey square, and the 2 x 3 and 2 x 1 to the light grey and white squares respectively).
Explanations will vary. Add together one side length from each square and then double your total. For example, for 62 – 42 : 2 x (6 + 4) = 20.
Another explanation is: Find the number in between the side length numbers and multiply by 4. For example, for 62 – 42 : 4 x 5 = 20.
Algebraically, this can be shown as:
where n is the side length of the smaller square.
b. 36.
102 – 82 = 2 x 10 + 2 x 8
Explanations will vary. For example, using the pattern described above: add 10 and 8 and double the total (2 x [10 + 8] = 36) or find the number between 8 and 10 and multiply it by 4 (4 x 9 = 36).