New Zealand Curriculum: Level 2
Learning Progression Frameworks: Geometric Thinking, Signpost 2 to Signpost 3
Target students
These activities are intended for students who recognise basic two-dimensional (flat) shapes and can name them using correct mathematical words, such as circle, triangle, and square. The students may identify the shapes by global appearance, and by seeing their likeness to known objects.
The following diagnostic questions indicate students’ degree of sophistication in classifying shapes by features then properties. A feature is a perceptual (visual) characteristic, such as straightness of sides or pointiness of corners. A property is pattern or consistency that connects features, such as all corners are ‘L’ shaped, or two sides are parallel. (show diagnostic questions)
The questions should be presented orally and in written form, so the student can refer to them. Students answer orally rather than in written form.
- Please tell me the name of each shape.
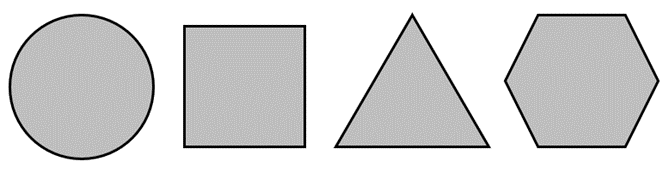
Why is the shape a ……?
Do you know something in the world that is a …….?
Signs of fluency and understanding:
Names all four shapes correctly using the mathematical words, circle, square, triangle, and hexagon. The student explains some features of each shape, such as roundness (circle), sharp corners, straight sides, and gives a real-life object of that shape, such as ball, mountain, biscuit, and honeycomb.
What to notice if they don’t solve the problem fluently:
Cannot name the shapes. This suggests the student needs opportunities to locate shapes in their environment and learn the correct mathematical names for those shapes.
Names the shapes but cannot explain what features they noticed in those shapes. This suggests the student needs experience with noticing and describing features of shapes.
Supporting activity:
Naming flat shapes and identifying features
- Find the triangles in this picture.
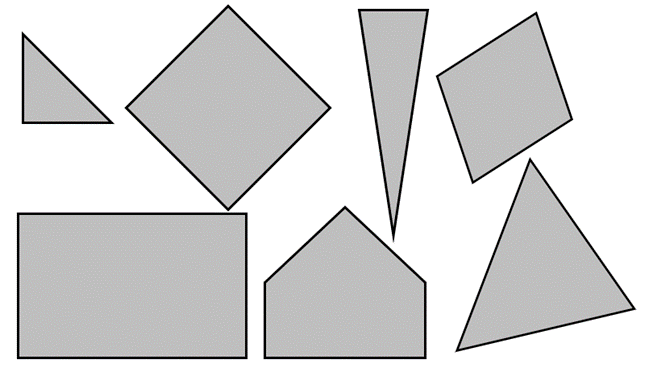
Tell me how you know those shapes are triangles.
Signs of fluency and understanding:
Correctly identifies all the triangles.
Explains that the identified triangle shapes all have three sides. Look for gestures, such as pointing, as well as language.
What to notice if they don’t solve the problem fluently:
Unable to identify any triangles or identifies only the most ‘prototypical’ triangles (bottom right or top left). This suggests that the student needs experience with identifying triangles of different kinds, sizes and orientations.
Selects all shapes with a top corner or horizontal base as triangles. This suggests that the student knows only the ‘prototypical’ form of a triangle (equilateral pointing upwards) and only attends to a single feature. The student will benefit from sorting shapes and identifying all the features of shapes they put together.
Supporting activity:
Identifying features
- Cut out the shapes on page 2 of the copymaster so they are each on a separate rectangular card.
Sort these shapes so that the shapes that are the same are in the same set (group).
Signs of fluency and understanding:
Sorts the shapes into categories (classes) based on common features or properties of the shapes.
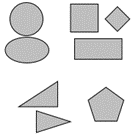
Explains the features or properties common to the shapes in each subset, such as:
“These two shapes are round.”
“These two shapes are triangles. They have three sides.”
“These shapes all have four sides, but this shape is turned around to look like a diamond.”
What to notice if they don’t solve the problem fluently:
Unable to create subsets and identify the common features or properties. This suggests the student needs experience noticing the similarities and differences between two shapes before working with more than two shapes. They need support describing the similarities and differences they notice using mathematical and everyday language.
Creates subsets without credible commonality in the shapes they put together. This suggests the student needs experience with sorting items by given features before progressing to sorting items by self-chosen features.
Supporting activity:
Sorting shapes by features and properties
- How are all these shapes the same?
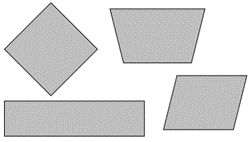
What differences can you see among these shapes?
Signs of fluency and understanding:
Recognises that all the shapes have four sides and/or four corners. May use the word quadrilateral to name the shapes (although this is not required). Finds differences in properties between shapes in a pair or difference among shapes in the whole set. For example:
“These shapes have L shaped corners (right angles). These shapes don’t”
“These shapes have matching sides” (meaning parallel). The student may use hand gestures to show parallel sides with palms together.
“These shapes have sides the same length and these shapes have different length sides.”
What to notice if they don’t solve the problem fluently:
Unable to identify any commonality in the shapes and see the shapes as all different. This suggests the student needs experience with identifying commonality in two shapes progressing to finding commonality in multiple shapes.
Notices that all four shapes have four sides but cannot identify any differences. This suggests the student needs experience with identifying differences between two shapes of similar appearance, before progressing to finding commonality in multiple shapes.
Supporting activity:
Sorting shapes by similarity and difference
- Someone put shapes that are the same into these two rings.
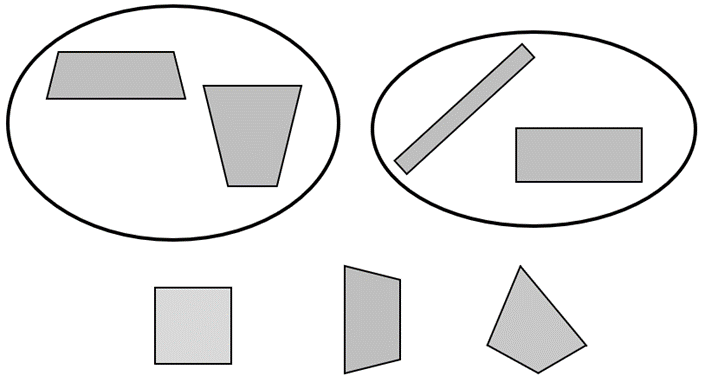
What is the same about the shapes in each ring?
There are three more shapes to sort.
Which ring does each shape belong in? Explain how you know.
Signs of fluency and understanding:
Establishes a credible criterion for shapes that belong in each ring. That may include naming the shapes as trapeziums and rectangles. The criteria might also include attention to properties without the mathematical names. For example:
“The shapes in this ring (left) do not have L corners. The shapes in this ring (right) have L corners.”
“The shapes in this ring have two sides like this (hands used to show parallelism) and another two sides like this. The shapes in this ring have two sides that are not like this (hands used).”
Allocating of the three shapes to rings is consistent with the criteria. The square belongs in the right ring (rectangles). The trapezium belongs in the left ring and the scalene quadrilateral belongs in neither ring. Students who use the angle criteria may place the scalene quadrilateral in the left ring.
What to notice if they don’t solve the problem fluently:
Unable to establish a legitimate criterion for inclusion in each ring so allocation of the three shapes is random. This indicates the student needs experience with classifying 2-dimensional shapes by properties, including finding examples and non-examples.
Supporting activity:
Classifying two-dimensional shapes
Teaching activities




