Pythagoras Power

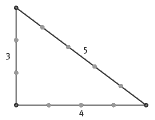
Pythagoras' theorem is the rule that enables us to find the length of a
missing side in a right-angled triangle. The Egyptians knew of the rule
and used it to square the corners of their fields, buildings, and the bases
of their pyramids. They used a piece of rope with knots spaced at equal
intervals. If they set the rope up around 3 pegs as in the diagram, they
knew that the angle opposite the longest side was a right angle.

Activity One

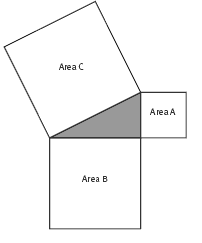
There are many ways of showing that Pythagoras' theorem is true, and this activity works through one of them. Students mark out, cut, and rearrange pieces from two squares of card to show that the square on the hypotenuse (area C) is equal to the sum of the squares on the other two sides (area A + area B).
For this demonstration to work, each student needs 2 squares of card the same size. They mark a point about a third of the way from the bottom left corner. There is nothing special about the third, but by dividing the side at this point, the students will get a triangle with sides that are clearly different lengths. This will make it easier for them to see what is happening. What is important is that the two lengths marked in diagram i are identical and that the 4 triangles in diagrams ii and iii are identical. When the students have finished the first three instructions, they should have the 4 triangles and a square. The students should note that the sides of the square have the same length as the longest side of the triangles.
In question a v, the students should see that they have 2 squares whose sides match the two shorter sides of the triangle.

In question b, the students need to compare the two arrangements, iii and v. The area of the background square is identical in each case, as is the area of the 4 triangles. So if you subtract the areas of the triangles from the areas of the squares, what remains in each case (the unshaded parts) must be the same. In other words, the sum of areas A and B must equal area C.
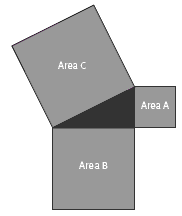
In question c, the students have to rearrange the squares around a triangle, as in the diagram, and then in question d describe what this arrangement appears to prove. They can use the term "longest side" instead of "hypotenuse" if they wish at this stage.
 

Activity Two

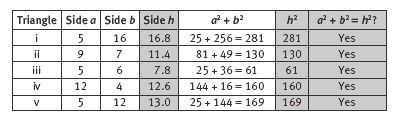
The students will need to draw the triangles in question 1 with care. If they use grid paper with centimetre squares, the grid will give them the right angles and the measurements of the two shorter sides. They should measure the hypotenuse with a ruler, accurate to the nearest millimetre. They can complete the table with the help of a calculator. Make sure that they understand how to use the square and square root functions. Also make sure that they remember to round h², to the nearest whole number, or they may have trouble seeing that a² + b² does equal h² in each case.

To answer question 2, the students use their understanding of the theorem (and a calculator) to work out that the hypotenuse must be very close to 30 centimetres. You could make up your own series of right-angled triangles and get the students to find the hypotenuse in each case. As an extension, you could challenge them to find a way of working out the length of a missing shorter side when the hypotenuse is  known.
 

Investigation
 

The most famous of all Pythagorean triples is (3, 4, 5), and there is an infinite number of others that are multiples of this one, for example, (6, 8, 10) and (30, 40, 50). There is also an infinite number of other Pythagorean triples, excluding multiples, most of which consist of very large numbers. 
As an extension, the students could investigate some other demonstrations of Pythagoras' theorem. For 43 different proofs of the theorem, see www.cut-the-knot.org/pythagoras/index.shtml.  

Answers to Activity

a. Practical activity
b. A and B together have the same area as C.
c. Diagrams should look like this:

d. Answers will vary, but the general idea is that, given a right-angled triangle, the combined area of the squares on the two shorter sides is the same as the
area of the square on the longest side.

Activity Two
1. a. Practical activity
b. Results in the grey columns come from measurement, so they may vary slightly:

2. 30 cm.
(h² = a² + b²
= 152 + 262
= 225 + 676
= 901.
Using the √ key, h = 30 [or 30.0] cm)
Investigation
Triangle v. An infinite number of other triples can be found. Many of these are multiples of others (for example, [5, 12, 13], [10, 24, 26], [50, 120, 130], and
so on). Here are the other "primitives" (those that are not multiples) that have a hypotenuse of less than 100: (3, 4, 5), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35,
37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (33, 56, 65),
(16, 63, 65), (48, 55, 73), (36, 77, 85), (13, 84, 85),
(39, 80, 89), and (65, 72, 97).