GM5-10: Apply trigonometric ratios and Pythagoras' theorem in two dimensions.
Elaboration on this Achievement Objective
This means that students will apply trigonometric ratios to find the angles and lengths of sides in right-angled triangles. Students need to recognise two features of trigonometric ratios:
- Given similar right angled triangles the ratios of side lengths are the same, for example
.png)
For both triangles the ratio of the sides opposite and adjacent to angle A is 6/8 = 0.75. For any similar triangle this is also true. This ratio is the tangent of angle A, so A = 37°.
- The trigonometric ratios can be found using a right-angled triangle with a hypotenuse of one and applied to any other similar right angled triangle by scaling.
The trigonometric ratios are:
- sin θ = side opposite θ/hypotenuse,
- cos θ = side adjacent to θ/hypotenuse,
- tan θ = side opposite θ/side adjacent to θ
These ratios are often remembered using the mnemonic SOH CAH TOA.
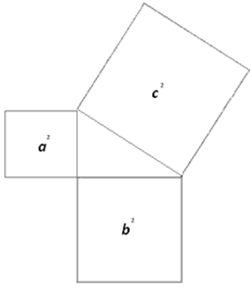
Students will use Pythagoras’ theorem (a2 + b2 = c2) to find the lengths of sides of right angle triangles.
Teaching resources for this Achievement Objective
The purpose of this multi-level task is to engage students in a task that requires them to apply geometric properties of polygons and right angles triangle techniques in solving for the area of a polygon.
Rich learning activities
Geometry and Measurement
Level Five
Construct two intersecting circles where the radius of the second circle is on the circumference of the first.Use Pythagoras’ theorem to find the area of a rhombusDevise and use problem solving strategies to explore situations mathematically (be systematic, draw a diagram, use a model)
Problem solving activities
Geometry and Measurement
Level Five
In this unit we look at various ways of measuring the height of an inaccessible object. The fundamental piece of mathematics used here is the ratio of corresponding sides of similar right angled triangles. The actual measurements needed relate to (i) an intermediately placed stick and (ii) the...
measure lengths and angles accurately find the height of objects using trigonometry
Units of Work
Geometry and Measurement
Level Five
This interactive learning module supports students to explore rules for the angle properties of intersecting and parallel lines.
Showing that a polygon is composed of rectangles and triangles. Showing that a non-right angled triangle is composed of two right-angled triangles. Given the length of one side, finding the area of a regular polygon.
Student e-Ako
Geometry and Measurement
Level Five
This unit supports students to learn and apply Pythagoras’ theorem and trigonometry in a context that enhances their engagement and produces an authentic and useful outcome. Students to create a resource “Goodnight Stories for Builders and Architects to be…” for other classes to use that puts...
Know some of the history behind Pythagoras’ theorem. Apply Pythagoras theorem in mathematical and real world contexts. Discover what sin, cos and tan are. Apply trigonometry ratios in mathematical and real world contexts.
Geometry and Measurement
Level Five
This unit introduces Pythagoras’ Theorem by getting the student to see the pattern linking the length of the hypotenuse of a right angled triangle and the lengths of the other two sides. Applications of the Theorem are considered, and students see that the Theorem only covers triangles that are...
find lengths of objects using Pythagoras’ Theorem understand how similar triangles can be used to prove Pythagoras’ Theorem understand that Pythagoras’ Theorem can be thought of in terms of areas on the sides of the triangle
Units of Work
Geometry and Measurement
Level Five
The purpose of this multi-level task is to engage students in using deductive steps, including the applications of Pythagoras' theorem to solve a problem.
Rich learning activities
Geometry and Measurement
Level Five
In this unit students will explore the importance of triangles, particularly right angled triangles, in the real world. Students will use practical measuring skills and calculations to find a pattern linking the ratio of the sides of a triangle with the angles. Introducing trigonometry using scale...
Measure the lengths of the sides of sets of similar right angled triangles and find the ratio of sides. Investigate the relationship between these ratios and the angle size. Use calculators or tables to find the sine, cosine and tangent of angles. Apply the known ratios of unit triangles (hypotenuse...
Units of Work
Number and Algebra
Level Five
Here we explore the cosine function, eventually using it to find unknown sides in right angle triangles.
Use cos to solve problems involving right-angled triangles Solve equations of the form cos(θ) = a, for a between –180 and 360 degrees State the value of cos(θ) in special cases Graph y = cos(θ)
Units of Work
Geometry and Measurement
Level Five
In this unit we explore the sine and related functions to find out specific values, relations between them, and applications.
use sin to solve problems involving right-angled triangles solve equations of the form sin(θ) = a, for θ between –180º and 360º state the value of sin(θ) in special cases graph y = sin(θ) describe some of the ways in which the sine, cosine and tangent functions are related
Units of Work
Geometry and Measurement
Level Five
In this unit we do a thorough exploration of tan, leading to the students being able to use tan to solve right angletriangles and to solve equations.
use tan to solve problems involving right-angled triangles solve equations of the form tan(θ) = a, for a between –180º and 360º degrees state the value of tan(θ) in special cases graph y = tan(θ)
Units of Work
Geometry and Measurement
Level Five
This is a level 5 geometry activity from the Figure It Out theme series.
solve problems using trigonometry solve problesm using Pythagoras
Figure It Out activities
Geometry and Measurement
Level Five
Find connections between numbers in a tableUse Pythagoras’ theorem in a general algebraic formMeasure accurately from a scale drawing.devise and use problem solving strategies to explore situations mathematically (be systematic, draw a diagram).
Problem solving activities
Geometry and Measurement
Level Five
This is a level 5 geometry strand activity from the Figure It Out series.A PDF of the student activity is included.
explore Pythagoras' theorem
Figure It Out activities
Geometry and Measurement
Level Five
This unit is an introduction to Pythagoras’ Theorem, including history, proofs, and practise in application of the theorem.
state and explain Pythagoras’ theorem use Pythagoras’ theorem to find unknown sides of right angled triangles
Units of Work
Geometry and Measurement
Level Five
use Pythagoras’ theorem to find the area of a rhombususe rulers and compasses to make a construction requiring perpendicular bisectorsdevise and use problem solving strategies to explore situations mathematically (be systematic, draw diagram)
Problem solving activities
Geometry and Measurement
Level Five
The purpose of this unit is to engage the student in applying their knowledge and skills of measurement to investigate gradients in practical situations.
Students develop their skills and knowledge on the mathematics learning progressions measurement sense, using maps and measuring tapes and/or supplied measurements to find, describe and use the steepness of a street. Students will be able to describe the steepness of a street in terms of a gradient...
Geometry and Measurement
Level Five
This unit follows on from others that introduce students to sine, cosine and tangent. In this unit students will gain practical experience in using trigonometry in practical situations; mainly outside the classroom.
describe and demonstrate how trigonometry can be used to find the height of a tall building or tree describe and demonstrate how trigonometry can be used to find the height of a high hill, or other high object where one cannot stand directly beneath the highest part describe in broad terms how...
Units of Work
Geometry and Measurement
Level Five
In this unit, students will explore the use of trigonometry to find unknown sides and angles in right-angled triangles, taking the concepts that were developed in the previous unit Introducing Trigonometry.
Label right angled triangles with respect to a given angle. Use trigonometric ratios to calculate the length of opposite and adjacent sides, and the hypotenuse in right angled triangles. Use trigonometric ratios to calculate the size of angles in right angled triangles. Maths skills required from...
Units of Work
Geometry and Measurement
Level Five