No three in a line

The Problem

Hannah has a square crate that can hold nine cartons of milk. Can she put six cartons into the crate so that no three of them are in a line? If so, in how many ways can she do it? If not, why not?

Teaching Sequence

1. Talk about milk crates and their symmetry.
2. Tell the class Hannah’s problem.
   What does no-three-in-a-line mean?
   Can you group four students so there are no-three-in-a-line?
   How many cartons is she going to use?
   Can you group five students so there are no-three-in-a-line?
   How might you go about solving Hannah’s problem?
3. Have the class work on the problem in their groups, and support them with useful prompts such as, Have you tried....?
4. As solutions emerge, compare the arrangements they have found. Have them to take turns in putting a picture of one of their arrangements on the board. Give each arrangement the student’s name to make reference easier in the discussion that ensues.
5. Ask:
   Are all of these arrangements different?
   How might we think of some of them as being the same?
6. As a lead into the extension problem, ask:
   How do you know if there are any more than we have found so far?
   How would you go about finding out more?
   How could you go about showing that there are no more?
7. Encourage students to see the systematic approach shown in the solution to get all possible answers.
8. Have some groups report back to the class. Select groups that have used different approaches to the problem. Display solutions.

Extension

Hannah has a square crate that can hold nine cartons of milk. Can she put five cartons into the crate so that no three of them are in a line? If so, in how many ways can she do it?

Solution

The students might be able to find a solution to this problem by guessing and checking. Give them time until they understand the problem, then encourage them to be more systematic.

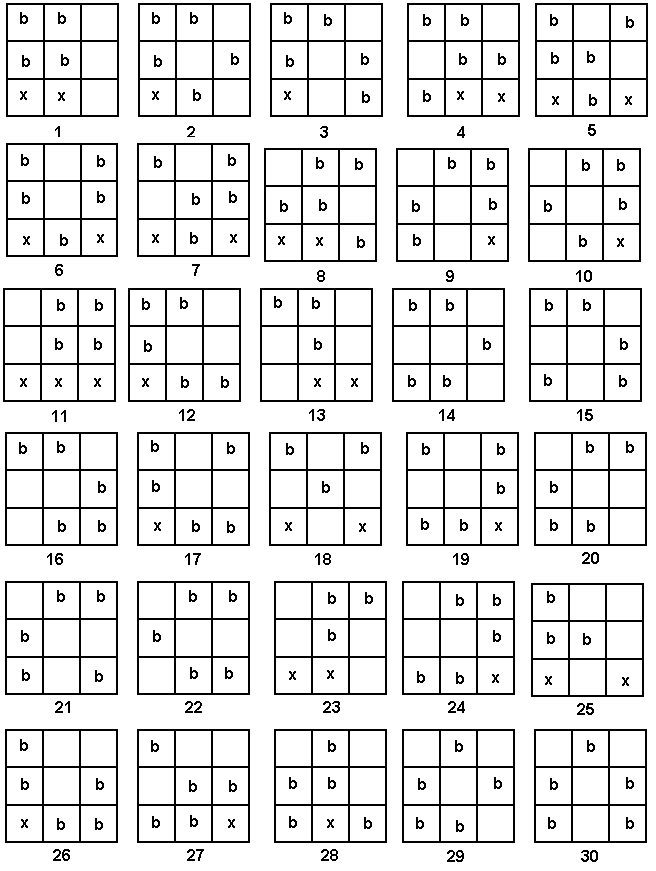
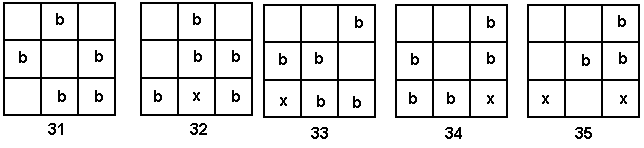
One systematic approach could involve recognising that there are two cartons in a row at most. Since 6 cartons are to be used, two cartons must be in each row of the crate. Start by putting two cartons together on the left of the top row of the crate. Then put one carton in each corner of the top row. The final case is with two cartons together in the right end of the top row. The crosses show that we can’t put cartons in those squares because that would give us three in a row (including diagonally).

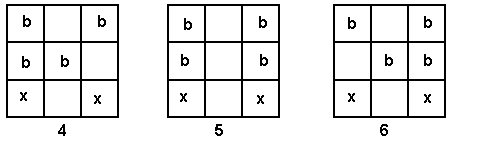
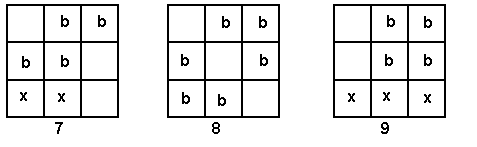
With position 1 the cartons in the second row are to the extreme right.  So position 1 leads nowhere.

With position 2 the cartons go two to the left and two to right. The cross shows that we can’t put a carton in that square because that would make three in a row. We can fill up the other two squares to give an answer.

With position 3 we put the two cartons in row two to the right-hand end. This forces two crosses and so there is no answer here.

The same arguments apply to the other positions. Only position 8 gives us another answer. However, by rotating 8 through a quarter turn (90° in a clockwise direction) it becomes the same as position 2. Both of these are alike (see Strawberry Milk.)

The answer to the original question is ‘yes’ and there is essentially only one possible answer.

Solution to the Extension

The students should be able to find some solutions to this problem by guessing and checking. Give them time until they understand the problem, then encourage them to be more systematic.

Note that as we can’t have three cartons in a row, there are at most two in a row. Since we have to use 5 cartons we have to have two rows with two cartons and one row with just one carton.  Start the systematic approach by putting two cartons in the top row and two in the next row. This is followed by two in the top row and one in the next; and then one in the top row.

There are many possibilities, however this systematic listing is useful.

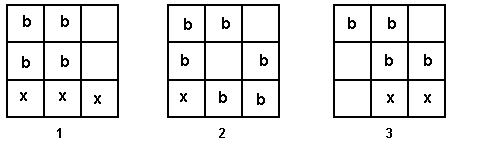
Out of all of that we get 28 possible answers. These are 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 17, 19, 20, 21, 22, 24, 26, 27, 28, 29, 30, 31, 32, 33, and 34. The question now is, how many of these are alike? So we need to group them into answers that are alike.

What answers are essentially the same as 2? We can get to 10 by one clockwise quarter turn, to 31 by another quarter turn and to 29 by another. So there is a class of four answers that are the same.

What answers are essentially the same as 3? Here we get 20, 24, and 26. The question now is, what about 9? Now you can’t get to 9 by rotating Hannah’s milk crate. You can get to it though by a reflection symmetry. But if you did that, the cartons would fall out of the crate. 9 is a different answer. It’s a left-hand form of 3. 

The list of answers that are the same as 9: 12, 16, and 34.

The rest.
4: 7, 28, 33;
5: 8, 27, 32 (this is the left-hand form of 4);
6: 14, 22, 30;
15: 17, 19, 21.

So Hannah can put 5 cartons in her crate in 7 different ways so that no three of them are in a line.