The purpose of this unit is to develop understanding of the processes involved in multiplying fractions.
- Solve problems involving finding a fraction of a fraction, using a regional model.
- Understand that the language ‘of ‘ and ‘times’ is interchangeable.
- Notice, explain and generalise what is happening to the numbers in a multiplication algorithm.
- Record, respond to, pose and solve a range of fraction multiplication problems.
- Understand and use number properties when multiplying fractions.
- Explore and demonstrate the reciprocal relationship between multiplication and division.
This unit builds upon students’ understanding of equivalent fractions, and of the addition and subtractionof fractions. As in earlier units of work, an emphasis is given to students modelling operations with fractions, using a range of materials to demonstrate their thinking, and recording using words and symbols. Having a sound knowledge of basic multiplication and division facts is fundamental to the students’ success in working with equivalent fractions and the multiplication of fractions.
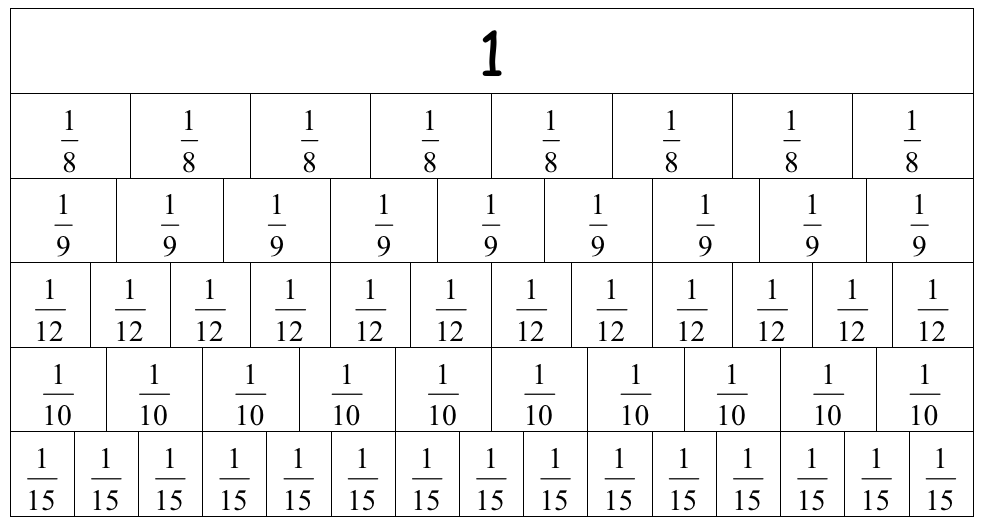
There are four key understandings that underpin multiplication of fractions. Firstly, multiplying two fractions involves finding the fraction of another fraction. For example, 1/2 x 1/4 can be interpreted as 1/2 of 1/4. Array models can be used to visualise and solve problems involving finding a fraction of a fraction, by breaking an area into parts(, horizontally and vertically). This scaffolds the move from a whole number to fractional understanding.
Secondly, when two fractions less than one are multiplied together, the product is always less than either factor. This presents a contrast for students who are used to multiplying whole numbers, as multiplying whole numbers often results in a product that is larger than either factor. Multiplying fractions requires a conceptual shift for the students who must clearly understand they are finding a part of a part.
Thirdly, by understanding the commutative property (i.e. the order in which numbers are multiplied does not change the answer), students can make problems simpler by changing the order of the factors.
Finally, to multiply fractions, students must recognise that the language of ‘times’ and ‘of’ are interchangeable.
Subdivision of fractions - or dividing an already-divided fraction into smaller pieces (e.g. 3/4 of 2/3) becomes a focus in multiplying fractions. Beginning with problems that involve working with unit parts without subdivision (eg. 1/3 of 3/8), establishes the conceptual understanding of the multiplication operation with fractions. Once this is clearly understood, working with unit parts that involve subdivision (eg. 3/4 of 2/3), focuses the students on recording and calculations as they explore the relationships between the numbers.
These ideas are presented in five sessions, which can be extended over a longer period of time if necessary. The sessions include complex concepts that are fundamental to a student’s success with fractions, meaning adequate time needs to be spent on developing understanding of each key idea. Whilst the games are introduced and used within sessions to consolidate ideas, they can also be added to the class or group independent activities, or be sent home for family challenges and enjoyment.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- varying the numbers used - higher or lower, simpler and/or more complex fractions
- providing equipment and visuals to manipulate and refer to
- providing prompts for written reflections
- providing teacher support at all stages of the learning
- grouping students to support each other or extend each other, and to provide further opportunities for students to explain their thinking and justify their analyses
- discussing prior knowledge of multiplying fractions
The contexts reflected in word problems in this unit can be adapted to suit the interests, experiences and culture of your students. Having students respond to the contexts you present, and create contexts of their own, will help them recognise the practical application of fraction multiplication. These contexts should reflect your current learning climate, the cultural knowledge of your students, and/or your students’ current interests.
- Fraction Strip sets
- Fraction strips
- Coloured fraction overlays
- Mini whiteboards and pens (enough for one per student)
- Copymasters 1, 2, 3, 4
Session 1
Activity 1: Finding a fraction of a whole number
- Begin this session by posing these three problems. These problems could be adapted to reflect the cultural makeup and learning interests of your students, or to reflect a current learning focus from another curriculum area. In pairs, have the students discuss their solutions to each:
- There are 33 children in Nina’s class. She was asked how many children would fit in the school van, if it could fit 1/3 of the class. She said 12. Is she right?
- 15 students in Jo’s class are travelling in the van to the kapahaka festival. This was 3/5 of the class. How many students are in Jo’s class?
- 18 students in Roly’s class are making poi for the kapahaka festival. 2/5 are decorating tī rākau. How many are decorating tī rākaru?
- On the class chart write:
Finding fractions of whole numbers.
Nina’s class: 1/3 of 33 is:
Jo’s class: 3/5 of something is 15 so 5/5 is:
Roly’s class: 3/5 of something is 18 so 2/5 is:
Have individual students come and record their results on the class chart and explain their solutions on behalf of their group.
Remind the students that they have been finding fractions of whole numbers.
Activity 2: Recognise that a fraction of a fraction results in a smaller part.
- Ask: What if you find a fraction of a fraction. Will the result be larger or smaller than both fractions?
Discuss (e.g. in pairs or small groups, or as a whole class). Record students' ideas on a class chart.
- Provide pairs of students with strips of paper and coloured pens.
Pose the problem: Can you use the materials to show one half of one half.
Have students share their results with another pair, and then ask some pairs to share with the class. Emphasise that the students now have a piece of paper that shows one-half and two-quarters.
Pose another problem: Use the materials to show three quarters of one half.
Have students share what they did and discuss the results. Emphasise that the students now have a piece of paper that shows one-half and three-eighths.
- Distribute Fraction Strips (Material Master 7-7) to the students to supplement the paper strips. Give students time to become familiar with the fraction strips reading the unit fractions shown and talking about the subdivisions that they see. A digital tool could also be used to demonstrate the movement and relative size of fraction pieces (search for ‘interactive fraction strip’)
Pose the question: What is one third of one half?
Ask students to find one half on the fraction wall and look for the subdivision of one half into thirds. Bring their attention to how one of the one-third pieces on the fraction wall could actually be divided into two, and encourage them to identify that one sixth is one third of one half.
E.g. I notice that the middle one-third piece doesn’t fit exactly within a one-half piece. The middle piece is split into two. What do you think these two new pieces would be called? Can you see any other fraction pieces on the fraction wall that would fit evenly into the middle one-third piece?
Distribute and discuss Copymaster 1. Explain that they can refer to the fraction wall or use the paper strips and scissors to complete it. Highlight the importance of their writing realistic stories for each (these can be linked to the same context that was used previously). You could provide some sentence starters for students struggling to generate a story (e.g. let’s start with the given fraction and write our story about people in our class - one quarter of the children…).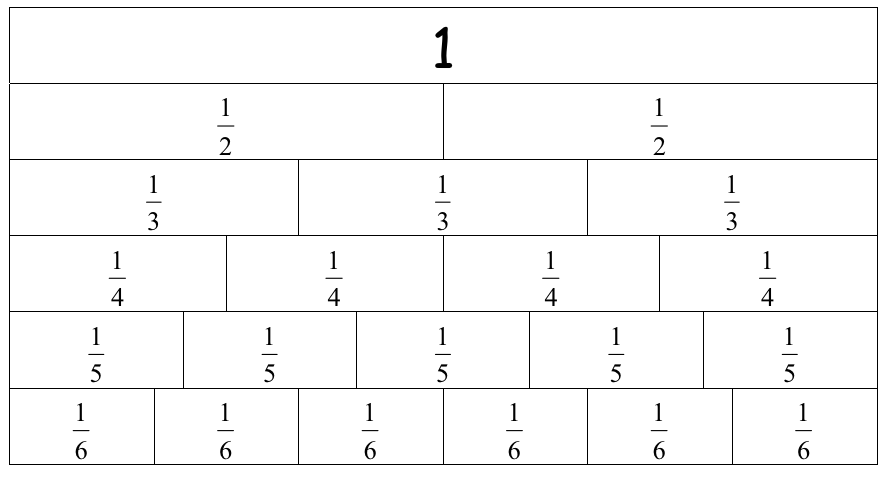
- Have students pair share and check their results.
Review the focus of the learning so far: We have been finding fractions of whole numbers and finding fractions of fractions of an area.
Activity 3: Solve problems involving finding a fraction of a fraction, using a regional model.
- Conclude the session by having a number of students read aloud (in random order) word problems they have written. The other students work in pairs to image paper strips or the fraction wall, and respond.
- Read these word problems (with relevant contexts reflected) aloud, and encourage the use of repeated addition to reach solutions:
One third of one half is one sixth, so what is two thirds of one half? (2/6 or 1/3)
One fifth of one half is one tenth, so what is three fifths of one half? (3/10)
One third of one third is one ninth, so what is two thirds of one third? (2/9)
One quarter of one half is one eighth, so what is three quarters of one half? (3/8).
- Conclude that a fraction of a fraction results is a smaller part. Students who understand this concept can be paired with students who are still developing their understanding of this.
Session 2
Activity 1: Understand that the language ‘of ‘ and ‘times’ is interchangeable.
- Refer back to problem 1 from session 1: There are 33 children in Nina’s class. She was asked how many children would fit in the school van, if it could fit 1/3 of the class. She said 12. Is she right?
Nina’s class: 1/3 of 33 is 11.
- Pose: Nina recorded the equation for this problem as 33 ÷ 1/3 = 11. Is she correct? Why? Why not? (33 ÷ 1/3 = 99 because there are 99 thirds in 33 wholes)
- Write 1/3 of 33 = 11 and 1/3 x 33 = 11. Ask students what they notice about the two equations. Draw attention to the difference being ‘x’ and ‘of’. ⅓ of 33 has the same meaning as ⅓ x 33 or 33 groups of ⅓. If we counted 33 pieces of ⅓ (e.g. on a fraction wall), then we would end up with 11 wholes. If necessary, continue to model this with smaller fraction equations and materials (e.g. ¼ x 4, ⅕ x 3, ⅙ x 4). Choose fraction equations that draw on students’ knowledge of basic multiplication facts, and that they can represent easily with materials or region models. Students ready for extension could generate problems for a partner to solve.
Activity 2: Record and respond to written multiplication equations.
Write on the class chart
1/4 x 2 = ?
2/3 x 12 = ?
Have students work in pairs to solve the problems, then share their results - including any pictures or diagrams used. Ask students to tell you what other ways these equations could be written (i.e. ¼ of 2, 2 lots of ¼). Draw diagrams to illustrate the concept, as necessary.
Activity 3: Record and respond to written multiplication equations.
Explore fractions of fractions:
Distribute think board sheets (Copymaster 2) to the students. Have each student complete a think board for each of the following two problems. Provide blank pieces of paper (e.g. a cut off piece of A4 or A3 paper) for students to use as fraction strips, where necessary. Look for students to divide the fraction strip into the necessary number of parts (i.e. that the denominator of the fraction that is being divided - tenths in 9/10). Students should identify the correct fraction on their strip (i.e. nine of those tenths) and then find the correct fraction (i.e. two-thirds). This will be quite a complicated process for some students and may require additional time and scaffolding. Students ready for extension could help a peer (tuakana-teina), create a poster or presentation to teach the class about the concept (ako), or create new questions for a peer to solve (mahi tahi).
2/3 x 9/10 = ?1/2 of 4/9 = ?
- Encourage students to use diagrams like those used for Copymaster 1.
They should look like this:
2/3 x 9/10 = 6/10
1/2 of 4/9 = 2/9.png)
Have students discuss and share their think boards with a partner.
Activity 4: Record and respond to written multiplication equations.
- Have students locate their copy of Copymaster 1 (Session 1, Activity 2, Step 3).
- Direct them to record written equations for each of the examples.
- Have students discuss anything they notice about the numbers in these equations (in which they are multiplying unit fractions). Emphasise that when we multiply whole numbers the product is larger than the factors, but when we multiply fractions the product is smaller than both factors.
Activity 5: Modelling the multiplication of fractions.
- Distribute a set of Fraction Overlays to each pair of students.
Give them time to explore the equipment, then ask pairs of students to demonstrate anything they have found out with the equipment.
- In their pairs, have students model several examples using the equipment, and record the diagram and equations on a mini whiteboard. Record some on the class chart. For example:
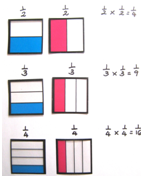


NB: In these examples, students recognise that the purple fraction is the result of multiplying the two factors. Ask your students to find the coloured areas which show the product (result) of multiplying the two factors.
- Pose these problems for the students to solve using the fraction overlays, recording each equation with factors and products as they do so. Remind students that ‘of’ and ‘x’ and ‘lots of’ have the same meaning in these questions, and encourage them to rephrase the equations as necessary (e.g. as ⅗ of ¾). Roam and support students as necessary.
3/5 x 3/4 = ?
2/3 x 2/5 = ?
1/5 x 1/4 = ?
5/6 x 1/2 = ?
- Conclude the session by summarising learning in this session on the class/group chart. For example:
When we are multiplying whole numbers the product is larger than both factors.
When we multiply fractions the product is smaller than both factors because we are finding a fraction of a fraction.
‘Of’, ‘times’ and ‘lots of’ are terms that can be used interchangeably - they mean the same thing.
Session 3
Activity 1: Introduction
- Begin this session by referring to the examples used in Session 2 and to your summary from the last session. Emphasise the following points:
- When we multiply fractions the product is smaller than both factors.
- The product is the result of the numerators being multiplied together and the denominators being multiplied together.
- Make Fraction Overlays available to the students.
Each pair should complete (at least one) A3 think board poster of one fraction multiplication problem, which includes a diagram of fraction overlays in the equipment section. These will be used for class display.
Activity 2: ‘Multiplifraction’
Students play the game Multiplifraction (Copymaster 3). See the attachment for instructions.
Activity 3: Record, respond to, pose, and solve a range of fraction multiplication problems.
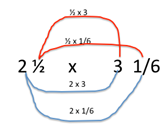
- Pose the problem: “Manu has 2 1/2 spare cans of paint left over from painting his house. He uses 3/4 of this to paint his shed. How many cans is this?”
Have the students explore the problem in pairs then bring their solutions to a class discussion. Provide fraction overlays and blank fraction strips for students to use. Consider pairing together students with mixed levels of mathematical knowledge and confidence to promote tuakana-teina (peer learning).
- Ask selected students to demonstrate their solutions on the class chart. Have students recognise two ways they can approach the problem:
3/4 x 2 + 3/4 x 1/2 = 1 1/2 + 3/8 = 1 7/8 (distributive property) or
3/4 x 5/2 = 15/8 = 1 7/8 (changing the mixed numeral into an improper fraction)
On the class chart draw what this would look like:.png)
- Have students work in pairs to explore each of these problems and show both ways of reaching the solutions.
“Maryanne 3 1/3 metres of fabric. She uses 2/3 this to make her dress for the school formal. How many metres did she use?”
“The floor area of Owen’s bedroom is 8 1/4 square metres. 3/4 of this is taken up with furniture. How many square metres of spare floor space does he have?”
- Have the students pair share both solutions for each of these problems:
2/3 x 3 1/3 =
3/4 x 8 1/4 =
Activity 4: Applying knowledge to word problems.
- Brainstorm some fraction contexts together then have each student write a word problem in which both factors are mixed numerals. (For example: 2 1/2 x 3 1/6). Guide them to use whole numbers less than 10.
As they each finish their own word problem, have them work on their solutions.
- Explore at least one word problem created by a student.
Highlight once more the two ways they can approach the problem:- changing the mixed numeral into an improper fraction.
- finding the sum of four partial products
For example: 2 1/2 x 3 1/6 - changing the mixed numeral into an improper fraction: 5/2 x 19/6 = 95/12 = 7 11/12 or
- finding the sum of four partial products
2 x 3= 6
2 x 1/6 = 2/6
1/2 x 3 = 1 1/2
1/2 x 1/6 = 1/12 - Show with a diagram like this:
- Finding the sum of the partial products: 6 + 2/6 + 1 1/2 + 1/12 = 6 + 4/12 + 1
6/12 + 1/12 = 7 11/12
- Take two other student created problems. Record these on the class chart or slideshow.
Have students work in pairs to solve the one of their choice.
- Have students pair share their solutions or digitally record and share them.
- Have students solve the other problem on their own, then record a reflection of the learning from this session. This could be included alongside their word problems and solutions.
Session 4
Activity 1: Understand and use number properties when multiplying fractions.
- Have the class/ group sitting in pairs on the mat. Begin by saying to one student so that all students can hear: “Please distribute scrap paper to each pair of students.” Write the word distribute on the class chart:
Ask the students to provide definitions of distribute and record their suggestions.
(If you are regularly adding to a class maths dictionary, you might like to record their ideas here. For example: ‘to spread’, ‘to share out’, ‘to give out’.)
Display this diagram from Session 3, Activity 4, Step 2, and write beneath it, ‘distributive property.’
Explain that this is the mathematical term for the process of expanding and solving the problem in this way.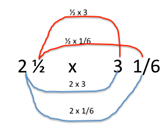
Ask why this might be called the ‘distributive property’ and record the students' suggestions.
- Have students suggest another fraction problem which could be solved by using the distributive property. Record suggestions.
Activity 2: Understand and use number properties when multiplying fractions.
- On the class chart record this equation and the questions:
1/4 x 1/2 = 1/2 x 1/4 True? False?
Require the students to work in pairs to decide on their answer (true or false) and, using the paper distributed in Activity 1, Step 1, to prove how they know in two different ways (eg. using an area model and an algorithm).
- Point out that one side of the classroom is the “true” side and the other is the “false” side. Have students indicate their thinking by moving to that side of the room.
- Ask a selection of students to justify their position, and show their ‘proof’.
- Consolidate this understanding by having 8 students stand in a group in the middle of the room.
Ask another student to show, by “using’ the group of 8 students what 1/4 of 1/2 equals. (1/8 or one student).
Reassemble the group of 8 students. Have another student “use” the group to demonstrate 1/2 of 1/4 (1/8 or one student).
Activity 3: Understand and use number properties when multiplying fractions.
- Query whether this works when whole numbers are involved.
Pose and write the problem 5 x 2/3 = 2/3 x 5 True? False?
Repeat Activity 2, Steps 1-3 above.
- Have 5 groups of 3 students stand in a group in the middle of the room.
Ask another student to show, by “using’ the five groups of three students model 2/3 + 2/3 + 2/3 + 2/3 + 2/3:
Ask 1/3 of the students in each group to sit down, leaving 2 students + 2 students + 2 students + 2 students = 2 students = 10. These students are then put back into groups of three making 3 1/3 groups. Reassemble the 5 groups of 3 students and combine them into one group of 15. Have another student “use” the group to demonstrate 2/3 of 5 groups (15 students) is 10 students. Have them regroup to make 3 1/3 groups.
Activity 4: Understand and use number properties when multiplying fractions.
- Write on the class chart: Commutative property. Explain that this is a common mathematical term for what has been happening in 2 and 3 above. Ask students to suggest what commutative might mean and record their suggestions. (‘to change place’, ‘to travel’) and confirm that it means that the order of the numbers can be changed without changing the result).
- Write on the class chart: Changing the order doesn’t change the result when we:
- add fractions. True? False? (true)
- subtract fractions. True? False? (false)
- multiply fractions. True? False? (true)
- divide fractions. True? False? (false) (encourage prediction)
- Have students discuss these in pairs, then, as a class, reach an agreement.
- Conclude the session by having the students suggest summary statements for today’s learning and record these on the class chart.
Session 5
Activity 1: Explore and demonstrate the reciprocal relationship between multiplication and division.
- Begin this session by reviewing conclusions from session 4.
Ask one student to: “Please distribute A3 poster paper to each pair of students.” Set a time limit and have students work in pairs to create a poster, which includes a story context, and which explains either the distributive or commutative property as it applies to multiplication of fractions.
(Alternatively, have students prepare an electronic presentation to explain either of these properties to parents).
- Early finishers can play Multiplifraction or fraction games from session 3.
Activity 2: Explore and demonstrate the reciprocal relationship between multiplication and division.
Ask students to form pairs. Distribute cards from Copymaster 4 to each pair. Have the pairs sort the cards into True and False piles. Pairs should then pair share, taking turns to read a card and talk about and justify their decision, using examples.
Activity 3: Explore and demonstrate the reciprocal relationship between multiplication and division.
- Conclude this session by reviewing class notes from each session.
- Pose this problem: 1/2 x 1/4 > 1/2 ÷ 1/4. True? False?
- Have students make their own decision independently.
- Select several students to explain their thinking.
- Conclude the session by indicating that they will be exploring this further in another session.
Dear families and whānau,
We have been learning about multiplying fractions and would appreciate your playing a game of Multiplifraction with your child. The cards are included in the pack. Your child will be pleased to explain the instructions for the game as it has been played in class. We hope you too will learn and enjoy.
