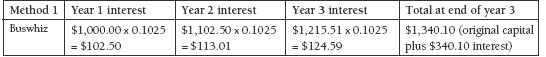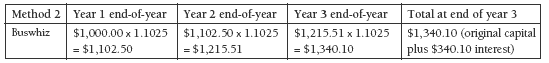This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework. It is also a level 3 statistics activity.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (803 KB)
find a percentage of a whole number (calculate interest rates)
Number Framework Links
These activities involve finding percentages of decimal amounts and calculating percentages. They are appropriate for students who are at stage 8 and should also be accessible for those at stage 7. Students who are at stage 6 will need a lot of scaffolding with the mathematics involved. It is desirable for students to
have had exposure to percentages before attempting these activities. It will also help them if they know the conversions between basic fractions and percentages, for example, that 10 percent = 1/10, and therefore know that calculating 10 percent of 300 is equivalent to finding 1/10 of 300 (= 30). (See the table of NDP material on
page 4.)
A calculator
Financial understanding
In this activity, Tavita finds out about different options available to him for investing the money from Granny and which options best meet his needs as an investor. The financial decision Tavita makes will determine how “well off” he will be in the future.
One dramatic approach to beginning this activity is to give a student an envelope with $1,000 in it and say You need to pay me back this loan in a year’s time. (You might prefer to use toy money!) Ask the students: How do you think I feel about lending this money? Encourage responses which consider the risk of not getting the money back. What would make it worthwhile then for me to lend this money? Discussion should centre round the idea of there being an incentive for lending the money. This incentive is called interest. What risks are involved in lending money? (The risk is that you might not get the money back.) What amount of interest is worth this risk? (This depends on a number of factors and explains why interest rates on offer are often different.)
Different banks and finance companies offer different interest rates. Check to see that the students realise that when you are investing your money, the higher the interest rate, the more money you make. If necessary, you can illustrate this using two students with a strip of paper each. This is the “initial investment”. The students
will invest at rates such as 10 percent and 25 percent. At the “end of the year”, students estimate the appropriate percentage increase (by matching the current size of the strip folded to the appropriate percentage) and tape it on. They repeat this the following year, and a third year, each time estimating from the new size of the strip.
The higher interest rate grows at a much faster rate.
NOTE: The term of investment guarantees the stated interest rate for the time of the term. A 3 year term deposit at 10 percent interest means the investment will earn 10 percent every year for 3 years, regardless of whether interest rates change. From the investor’s perspective, longer term deposits are a good idea if interest rates are
expected to drop and shorter term deposits are better if interest rates are expected to rise.
Before beginning the activity, some students will need help from you to understand the investment table. Some questions which may help with this are:
What are the different investment companies in this table? (Growgroup, Earnlots, Buswhiz, Bingcorp, Farmbankers, Financeinc, and Myson.)
What does minimum amount mean? (This is the minimum amount of money that can be invested in the company.
Tavita will not be able to invest with XYZ bank because he does not have $10,000.)
What does a 3 year deposit entail? (The money invested is locked in for 3 years – that is, the investor will not be able to access their money before then without facing penalties. It will earn the stated interest rate each year.)
Why do you think companies offer different amounts of interest for different terms of deposit? (The longer the company has the money invested with them, the longer they have to use that money for their business purposes. Often companies will offer a higher rate for a longer term as an incentive for people to invest for a longer time.)
Mathematics and statistics
Following this discussion, some students will be able to complete the activity independently, others will need your assistance. Question 1c is the most challenging and may well need teacher assistance for all students.
To be successful with question 1c, students need to have completed the activities on pages 10–11. They need first to be able to convert the percentages into decimals, 10.25% = 0.1025; 9% = 0.09; 8.5% = 0.085. (These can be found by dividing the percentage amount by 100.) They could discuss in groups the various methods for
calculating the answers to this question. Here are three methods for calculating compound interest:
Method 1 involves calculating the interest and adding it to the capital at the end of each year. For example:
Method 2 involves calculating the new capital (with interest added) by multiplying by one whole plus the interest. For example:
Method 3 involves calculating three years of interest plus capital all at once. For example:
The students may need to discuss question 2 with you. See the notes in the Answers section.
Extension
As an extension, the students could find the current investment rates in the newspaper. Ask Which would be Tavita’s best option today?
Financial understanding
Some students will be interested in further discussion regarding why banks offer different rates, including term of investment, and how the risk for the investor affects their decision. (Many students will be able to complete the activity now and will not be interested in further discussion.) These ideas can be illustrated with the
following skit: The prince of Dodgyland has just emailed my financial adviser an offer of 25 percent interest rate for an investment in his personal bank. What a fabulous rate! I’ve saved $1,000. Should I invest this in this bank for a year?
Hopefully, students will suggest ideas pertaining to the risk level of the investment. Although 25 percent provides a great return on investment, the chances of the bank going under are perhaps very high. In New Zealand, banks are a very low-risk investment because it is extremely unlikely that a bank will become bankrupt.
Students may wish to investigate what happens when a finance company does become bankrupt.
Social Sciences Links
Achievement objective:
• Understand how people make decisions about access to and use of resources (Social Studies, level 3)
Ask (for Activity One) What factors other than interest rates should Tavita consider before he invests money with a company?
Students could research interest rates in other countries and compare them to New Zealand’s rates. This could lead into an investigation of the role the Reserve Bank plays in setting interest rates and the various effects on the economy of having high or low interest rates. Students could investigate what rights and responsibilities the banks in New Zealand have and what rights and responsibilities consumers have in New Zealand when dealing with banks. Ask Who and what “protects”
(governs) these rights and responsibilities?
Answers to Activity
1. a. Buswhiz, Bingcorp, Financeinc, Myson. Tavita has $1,000 to invest, but the
minimum amount for the other companies is more than that.
b. Buswhiz: 3 years; Bingcorp: 3 years; Financeinc: 1 year; Myson: 1 year. (Those
terms give the highest interest rates for each company.)
c. Approximately $340 (Buswhiz), $295 (Bingcorp), $277 (Financeinc), and $295
(Myson)
2. a. With a 6 month term, money is not “locked in” for as long. You can choose a different investment after 6 months if you wish. However, the rate of interest is not as high as for longer time periods.
b. A 3 year term may offer better interest rates than shorter terms. However, your money stays at that interest rate for the 3 years, even if 3 year rates go up (or down) after you have invested your money. If you decide to access your money early, you pay a penalty.
Reflective question
Answers will vary. For example, you can talk to qualified financial advisers, evaluate information in newspapers and on the Internet, talk to the appropriate bank staff, or join an investment group.