In this unit students take part in a variety of measurement tasks including measuring the length of a slinky, working out how many slices of tomato will fit around the edge of a pizza and accurately drawing the label from a can.
- Describe a method to measure the length of circular objects.
- Measure length using metres, centimeters and millimeters.
- Calculate the circumference of a circle from a measurement of diameter.
The measuring challenges in this unit invite students to engage in practical measuring tasks. In all tasks students are presented with a variety of measuring tools to complete the task and are asked to plan a method to solve the problem. Emphasis is on the measurement process, not the answer obtained, with students encouraged to describe their solutions and the thinking behind them. As these tasks involve measuring the circumference of a circle it would be appropriate to introduce the formula for this as a way of checking the measurements obtained.
You can support the exploration of the relationship between diameter and circumference by collecting together various sized circles. Give out the circles to pairs of students. Ask students to use a piece of string to measure the diameter of their circle. Use another piece of string to stretch around the circumference. Ask students to explore how many times longer the circumference string is compared to the diameter string. Compare the results for each group. They should find that no matter the size of the circle the circumference is always 3 and a bit times longer than the diameter. Having done this type of exploration the introduction of the formula will have more meaning.
Circumference = π x diameter
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- Physically measuring real objects and comparing measures. For example, using a length of string to get a measure of diameter of a circular object then mapping that length around the circumference.
- Explicitly model techniques such as measuring lengths for students who need support.
- Representing the problems diagrammatically to reduce the cognitive load.
- Use calculators to reduce the burden of calculation.
- Ask students to work in collaborative teams to distribute the workload and share ideas.
The contexts for this unit are variable situations in which circles are used. Slinky toys, cans and pizzas are likely to be part of your students’ worlds. Contexts can be altered to meet the personal, social, and cultural interests of ākonga. Possibly use other non-food-related circular objects like bicycle wheels, clocks, CDs, playground equipment, plates, hoola hoops, and tree stumps. Students might investigate the method of joining hands used by pre-European māori to measure the circumference of a tōtara or kauri tree. Measurement was used to choose trees to make waka.
- Scissors
- Paper strips
- String
- Rulers: metre, 30 cm or a tape measure
- Paper and pencils for working
- slinky
- a variety of cans, with labels attached
- large pizza bases, or a paper circle to represent these ·
- Doughnuts: round and straight
- Several balls, netball size of similar. Ideally all balls the same size.
- Large sheets of paper, A1 size is ideal
- Copymasters One, Two, Three, Four, Five and Six
Station One
In this station students work together to devise a way to measure the length of slinky: a coiled plastic toy. They will need to consider how to measure each ring and then multiply by the number of rings on the slinky, allowing for partial revolutions. Copymaster 1 contains student instructions for this activity.
Encourage students to plan their method for measuring before they begin and reflect on its success when finished. Introduce students to the formula for circumference as a way to check their measurements. (Circumference = π x diameter).
Have them measure the diameter and multiply this by pi (approximated by 3.14) to get a calculated circumference of one revolution. They can then compare this with the measurement made for one single revolution of the slinky.
Station Two
Students draw a diagram of the label on a can, taking measurements from the can to ensure their diagram is accurate. Diagrams can be drawn to any scale with the simplest being a one to one representation; alternatively you could specify a scale such as 2:1 or ask students to choose their own.
Students plan their method before they begin and assess its success at the end of the task. Possible methods include:
- Using a piece of string or paper strip to measure around the can and directly transferring this length to the diagram.
- Using a piece of string or paper strip to measure around the can, measuring the piece of string in cm and mm and using a ruler to draw the appropriate length line on the diagram.
- The height of the label can be measured directly using a ruler.
Students can verify the circumference by calculating the circumference of the can. Have them measure the diameter and multiply this by pi to get a calculated circumference.
Once all groups have finished this activity measurements can be checked by removing the label from the can for direct comparison with the diagrams drawn if the scale used in the diagram is one to one. Copymaster 2 contains student instructions for this task.
Station Three
In this station students estimate, then measure, how many slices of tomato will fit around the edge of a pizza. As students work encourage them to focus on the method used for measurement, planning their approach before they begin and evaluating it at the completion of the task. Copymaster 3 contains student instructions for this activity.
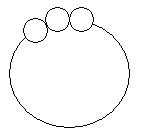
Note that students will need to consider how far from the edge of the pizza the tomato is placed. Using the diameter of the tomato pieces and the outside edge of the pizza base as the basis for the measurements will not work as tomatoes would then be hanging over the edge of the pizza. Students will need to measure the circumference of the pizza base at least 3.25 cm from the edge to allow for the width of the tomato slices.
 |
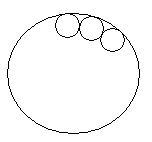 |
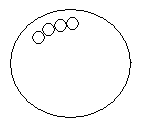 |
| Using the diameter of the tomato pieces and the outside edge of the pizza base as the basis for measurements. | Using the diameter of the tomato pieces and 3.25cm from the edge of the pizza base as the basis for measurements. | Using the diameter of the tomato pieces and greater than 3.25cm from the edge of the pizza base as the basis for measurements. |
Students could verify their answers by
- calculating the circumference of the position on the pizza base the tomatoes are to be placed. Have them measure the diameter across the pizza from the middle of the tomatoes and multiply this by pi to get a calculated circumference.
- Making circles of 6.5 cm diameter to represent the tomato and place them on the pizza base
- Repeating their measurements
Have students compare and justify results with other groups once the task is complete.
Station Four
Students measure the length of round and straight doughnuts to work out which is longer. The focus of the task is on the method used for measurement with students asked to describe their method as well as solve the problem. Copymaster 4 contains student instructions for this activity.
To complete this task, students will need to devise a way to measure the length of the round doughnut. One way would be to use a piece of string to measure around the doughnut and then measure the length of the string. Students will come up with other options. Encourage them to explore different methods. Students who complete this task easily could be challenged to draw diagrams of doughnuts in which the round and the straight ones are the same length.
Students can verify the circumference by calculating the circumference of the doughnut. Have them measure the diameter and multiply this by pi to get a calculated circumference.
Station Five
In this station students work out the minimum amount of wrapping paper required to cover a ball. The focus of the task is on the method used for measurement with students asked to describe their method as well as solve the problem. Copymaster 5 contains student instructions for this activity.
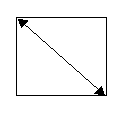
Students need to decide on the shape of the paper they will use. A square is the simplest but they may come up with other options, encourage them as they explore alternatives. If using a square of paper, the circumference of the ball can be used as either the length of the sides of the square, or the diagonal measurement. Using the diagonal measurement will result in less wrapping paper being used.
 |
 |
| Circumference of ball equals diagonal measurement of wrapping paper square. Less paper used. | Circumference of ball equals length of one side of square of wrapping paper. More paper used. |
Measurements will also need to allow for some overlap of paper. Discuss with the students what an appropriate overlap might be.
When students have finished the task have them cut out a piece of paper to the measurements they have worked out and try to wrap the ball. Is it possible? Would they change their answer now they have tried it? If so, what false assumptions were made in the measuring process? Students could make comparisons using the formulae for the surface area of a sphere. S = πd2
How much of the wrapping paper is not in direct contact with the ball?
Family and whānau,
This week your child has some measuring work to do with circles. Ask them to explain the steps they have gone through to solve this measuring task.
- Find a round object at home. You could use the wheel of your bike, the rim of a pot, the edge of a lampshade or anything else you can find.
- Estimate the length around the outside of the circle, this is called the circumference.
- Plan a way to measure the circumference, including the tools you will use.
- Measure the object using your plan. Record your answer.
- Can you think of a way to check your measurement?