This counting collections activity engages students in finding how many handshakes there would be if everyone in a group shook hands with everyone else.
When a count forms a pattern, students can be encouraged to generalise. A generalised pattern supports students to reason algebraically (develop a rule) for the further counts in the pattern.
Counting collections promotes number sense, and is an essential foundation for students to be successful mathematicians. Recent literature (e.g. Boaler, 2008) suggests that flexible grouping practices best supports equitable opportunities for student learning.
It is important to share the mathematical focus of the task with students. Provide them with opportunities to find patterns within their count, to work collaboratively, to record their patterns and strategies and to share and justify their mathematical thinking using a variety of representations. The progression in the sophistication of students’ thinking when asked to count a collection of objects goes from counting in ones, to counting in groups, reasoning additively to reasoning multiplicatively. When the count forms a pattern (e.g. how many squares or the handshake problem), students should be encouraged to generalise and reason algebraically (develop a rule) for the nth count in the pattern.
Consider the mathematical language your students are likely to use when grouping and counting and the language you want to develop.
Student agency is promoted if students have choice over their own counting and recording methods. Rather than suggesting particular solutions or counting methods to students, teachers can use enabling prompts to support students who require assistance. Extending prompts can be offered when students have completed the task to build more sophisticated strategies and understandings.
- Manipulatives (e.g. counters, hundreds boards) to facilitate acting out the problem or recording the solution.
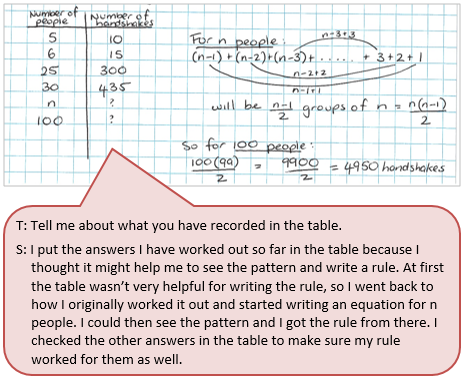
 Task Introduction
Task Introduction
The wondering for this mathematical inquiry is:
- I wonder how many handshakes there would be if everyone in the room shakes hands with everybody else once.
Considerations when planning for the task introduction include:
- Do the students understand the context of the task?
- What key mathematical ideas and language do teachers need to clarify with students in order for them to engage with the task?
Student Exploration of the Task
- While the students are exploring the task, listen to their mathematical thinking and language particularly around noticing patterns.
- Encourage students to record their thinking in a systematic way that illuminates possible patterns and encourages generalisations.
Students can formulate and check possible generalisations.
- If students are struggling to get started, enabling prompts can be offered but only once students have had sufficient time to struggle with the problem themselves.
Examples include:
How many handshakes just at this table group?
What if we add another person to the table group? And another one?
Record your findings in a way that we can see if there is a pattern.
- Extending Prompts can be offered if students finish quickly or find the task easy. They encourage higher order thinking and generalisation within the same task.
Examples include:
What patterns have you noticed in your count?
Record the patterns so that you can share them with others.
Use your generalisation to find how many handshakes if there were 100 people.
Find a rule that would work for any number of people.