These are level 3 number, statistics, and algebra problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (280 KB)
use addition and a systematic approach to solve puzzles (Problem 1)
find outcomes using a diagram (Problem 2)
use algebraic thinking to solve problems (Problem 3)
Problem One
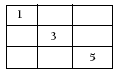
The information that the students have to work with is that a 3 goes in the centre square and that there is only one 1 used somewhere else. The 1 can go either in a corner or in the middle of one of the four sides of the square. Putting it in a corner will mean that a 5 will go in the opposite corner.
The two missing numbers in the top row must add up to 8, the two missing numbers in the middle row must add up to 6, and in the bottom row to 4. The bottom row is the best one to fill in next because there is only one possible option for this row:
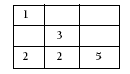
The numbers must be 2 and 2. The other two pairs of numbers that add up to 4 are 1 + 3, which is not possible because you can use only one 1, or 4 + 0, which is not possible because you can’t use 0 (you have to use positive numbers).
But from here, you come to a dead end for several reasons. The only option for the right column is another two 2s, which means the middle square in the top row must be 6, which makes the middle column add up to 11, which is too high. Also, the only option for the middle square in the left column is 6, which would mean the middle square in the right column would have to be 0, which is not possible.
There is no point trying the 1 in another column because, due to the symmetry of the square, you will end up at the same dead end, with the numbers being a rotation or reflection of the attempt above.
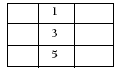
With the 1 in a middle square you can get this (and rotations and reflections of this):
Following the reasoning given above, the other two numbers in the bottom row must be 2 and 2, and this allows you to fill in all the other squares:
Explained like this, the problem seems fairly straightforward, but it will probably take the students quite a lot of trial and improvement to work it out. Carefully thinking through all the options and the effects of all the options will make their working more efficient. For example:
• When there are several squares to fill in, first fill in the squares where there is only one possible option (such as the two 2s either side of the 5 in the examples above).
• Think about the numbers that you can use. Using another 5 will mean using another 1, and this is not possible, so there must only be one 5. As explained above, 6 and above are not possible because it would mean using a 0 as well and you can use only positive numbers.
• Consider the effect of rotation and reflection (such as trying a 1 in a different corner). As explained above, this will also lead to a dead end.
Problem Two
This question is similar to Problem Four, page 11. There must be five tracks from any village to any other village. There are six villages, so it looks as if there are going to be 5 x 6 = 30 tracks. However, this method has counted every track twice. (The one from Zeebe to Uba was counted when you counted the tracks from Zeebe, and it was also counted when you counted the tracks from Uba.) So there are actually 15 tracks on Circuit Island.
Extension
“What if there were 100 villages on the island?”
Problem Three
a. There are 32 marbles altogether. If there is to be an equal number in each jar, there has to be eight marbles in each. The simplest way to do this is to take two marbles from the yellow jar and one from the green jar and put all three marbles into the blue jar.
b. The students can build on their working for part a to find the answer for part b. There are 32 marbles and 4 jars, so there is an average of 8 marbles in each jar. The two middle jars (blue and yellow), which have a difference of two marbles, will have the numbers either side of 8, that is, 7 in the blue jar and 9 in the yellow jar. The red jar will have 5 marbles, and the green jar will have 11 marbles. Check: 5 + 7 + 9 + 11 = 32.
Note that because there are an even number of jars, none of the jars in this scenario will contain the average number of marbles. This might be slightly difficult for the students to grasp. They would probably find the problem easier if there were an odd number of jars, in which case the middle jar would contain the average number of marbles. For example, if there were three jars: the first has two fewer marbles than the second and the second has two fewer marbles than the third. Altogether, there are 30 marbles in the jars. How many in each jar? There’ll be an average of 10 marbles in each jar, so there’ll be 10 in the second jar, 8 in the first jar, and 12 in the third jar.
Some students may approach the problem algebraically:
r = number of marbles in red jar
b = r + 2
y = r + 4
g = r + 6
r + b + y + g = 32
r + (r + 2) + (r + 4) + (r + 6) = 32
4r + 12 = 32
4r = 20
r = 5
so b = 7, y = 9, and g = 11
If the students have trouble with these strategies, they could use trial and improvement to find four consecutive odd numbers that add up to 32.
Problem Four
This problem is very similar to Activity One, page 23, in Measurement, Figure It Out, Level 3.
You could give the students this activity first as a warm-up. Refer also to the teachers’ notes for this activity.
a. If you cooked four patties on both sides and then the remaining two, the time taken would be 5 minutes plus another 5 minutes = 10 minutes. However, the following steps show a different story:
• Place four patties on the griller.
• After 3 minutes, flip two of the patties and remove two (place in a warmer). Add the two remaining patties.
• After 2 minutes, remove the two patties that are now cooked on both sides.
• After another minute, flip the two remaining patties and add the two “half-cooked”
patties that were placed in the warmer.
• Remove the four patties after a further 2 minutes.
Total time elapsed is 3 + 2 + 1 + 2 = 8 minutes.
Notice that if there were five patties, the same method would work if you split the patties into one group of three and another of two. After 3 minutes, two of the cooking patties would be flipped and the other placed in the warmer while the two remaining raw patties would be started up. If, on the other hand, there were seven patties, nothing would be gained. It would take 10 minutes to cook seven patties, just as it would for eight.
b. It would take 13 minutes to cook 10 patties. This is because 10 = 6 + 4.
It takes 8 minutes to cook six patties (shown above) and another 5 minutes to cook the remaining four. So the time needed is 8 + 5 = 13.
Extension
An extension question could be: “How long do you need to cook 25 patties?”
The most efficient patty cook-up is when you have multiples of 4. 25 is not a multiple of 4. The situation that wastes time is when one patty has to be cooked alone, so breaking 25 up into six lots of four with one remaining is not efficient. But by cooking five lots of four and then the remaining 5, you can do it in 5 x 5 minutes + 1 x 8 minutes = 33 minutes. The same could be achieved by grouping as follows:
Four lots of four, one lot of six, and then the remaining three patties gives
4 x 5 + 1 x 8 + 1 x 5 = 20 + 8 + 5
= 33.
Hints for Students
1. Try placing the 1 first. Work systematically to fill in the other squares.
Experiment with different arrangements of numbers.
2. Can you find a quick way to count the tracks?
Try a smaller case first.
3. Start by counting all the marbles. What will you need to do to find out how many marbles need to go in each jar?
You could use trial and improvement to find the answer for part b, but can you find a quicker way to find the answer?
4. Experiment. Possibly try a smaller number of patties first.
For part a, cooking four patties on both sides and then the remaining two patties on both sides is not the quickest way to cook the patties.
Answers to Problems
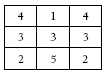
1. One way of setting out the solution is:
Note that the order of the rows and columns could change with rotation or reflection.
2. 15, including existing tracks
3. a. Two from the yellow jar and one from the green jar go in the blue jar, making eight marbles in each.
b. The red jar has 5, the blue jar has 7, the yellow jar has 9, and the green jar has 11.
4. a. 8 minutes
b. 13 minutes