This unit looks at Fibonacci numbers and how they occur in nature. Fibonacci numbers provide a rich context in which to apply algebra at Level 4. It is recommended that students already have some experience with Level 4 algebra, prior to the introduction of this unit.
- Use a recursive rule to generate the sequence of Fibonacci numbers.
- Create a Fibonacci spiral using squares with Fibonacci side lengths.
- Find a pattern of odd and even numbers in the sequence.
- Identify and represent patterns we find for consecutive numbers in the sequence.
In this unit we look at Fibonacci numbers and how they occur in nature. We also look at situations where the next number in a sequence is created by adding the previous two numbers. We explore some intriguing patterns that occur with the Fibonacci sequence and try to explain why some of those patterns occur.
Fibonacci numbers are a specific example of sequences that are generated by rules that dictate how to operate on the previous term to get the next term. Such rules are called recurrence relations because they can be applied infinitely in a ‘recurring’ way. The Fibonacci sequence is created using the recursive rule Fn = Fn-2 + Fn-1. That rule means that the nth Fibonacci number is the sum of the previous two Fibonacci numbers.
The sequence progresses as 1, 1, 2, 3, 5, 8, 13,.. Other sequences can be created using the same rule but different starting numbers, e.g. 2, 1, 3, 4, 7, 11, … (Lucas numbers).
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- physically acting out scenarios using people or materials. This could include creating a family tree of direct relatives with class members
- using recording tools such as tables and branch diagrams (featured in the PowerPoints, and of your own creation in response to students’ needs) to support students’ search for patterns
- pacing the sequencing of patterns appropriately allowing time for students to discuss their predictions with others
- using calculators to ease the cognitive load associated with making calculations with larger whole numbers, so students can focus more on pattern and less on finding answers
- providing opportunities for students to work in mixed groupings, pairs, as individuals, and with the whole class. This will allow them to benefit from the sharing and justification of ideas, collaboration (mahi tahi) and peer learning (tuakana teina)
- providing opportunities for students to demonstrate their learning, and scaffold the learning of others, through the creation and sharing of presentations that reflect their understanding (e.g. digital, paper, audio, oral)
- directly and explicitly instructing students on key foundational concepts, such as square numbers, consecutive numbers, the golden ratio.
The contexts for this unit are, and can be, varied. The Fibonacci sequence is found in a variety of natural and human-made phenomena, which is reflected throughout this unit. Investigate related situations that are of interest to your students, such as Fibonacci in human proportion, in spirals (fern fronds), in nautilus shells, and in the construction of famous buildings. Students might investigate Fibonacci in real life situations and apply the sequence to a situation in their life.
Te reo Māori kupu such as raupapa (sequence) and ture (rule, formula) could be introduced in this unit and used throughout other mathematical learning.
Lesson One
In this lesson we explore how to generate the Fibonacci sequence. Show the students Slide One of PowerPoint One. After the first sequence, show the tree growing until it has 13 branches.
Watch carefully how the tree grows new branches each spring.
Is there a pattern to the growth?
How many branches will the tree have after next spring?
Click on the mouse to reveal that the tree has 21 branches next spring.
Do students notice that each new branch does not sprout another branch until its second spring?
Do they notice that each new number of branches is the sum of the two springs before it?
Progress to Slide Two which shows the growing family tree of a male bee. Male bees have only one parent, a mother (female). Female bees have two parents, a father (male) and a mother (female). Watch the animation until three generations are past. Comment that some plants sprout in this manner, though often conditions like weather and animals mean that branches get lost.
How many ancestors are in the family tree after five generations?
Ask students to draw the family tree to five generations. Slide Three has a model answer. Create a table of values for the numbers of ancestors and their genders.
| Generation | Male ancestors | Female ancestors | Total number |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 1 | 2 |
| 3 | 1 | 2 | 3 |
| 4 | 2 | 3 | 5 |
| 5 | 3 | 5 | 8 |
Ask the students to consider what will happen in the next two generations:
- Each male ancestor will have only a mother.
- Each female ancestor will have both a mother and father.
- There will be a female ancestor for each bee in the layer below, but a male ancestor only for each female bee.
The next layers of the table are:
| Generation | Male ancestors | Female ancestors | Total number |
| 6 | 5 | 8 | 13 |
| 7 | 8 | 13 | 21 |
Students should note that the same sequence of numbers 1, 2, 3, 5, 8, 13, 21,…, occurs in the tree branching pattern and the bee’s ancestor patterns.
What is similar about both situations?
Students might note that extra branches or ancestors are added by splitting into two. They might also observe that there is a delay of one spring or generation. Branches must wait one spring before sprouting other branches, and male bees must wait one generation before they have another female male ancestor.
Slides 5 and 6 show Fibonacci numbers appearing in the growth spirals of plants. The pinecone has 13 rows of bracts spiralling outwards. Similarly, the aloe vera plant has 5 spirals of leaves. The pineapple has 8 rows of scales spirally from the base to the top. 13, 5, and 8 are Fibonacci numbers.
Given the frequency of Fibonacci numbers appearing as spirals in nature it is no surprise that these same numbers can generate a beautiful spiral. Slide 9 shows how to create the spiral using arrangements of squares with sides lengths that are consecutive Fibonacci numbers. Copymaster One is provided for students to create their own spiral pattern. Slides 10-12 show examples of where the spiral occurs in nature.
Slide 13 shows the areas of the squares in the spiral design appearing. Click once for the areas to appear in sequence.
What do these numbers represent?
You may need to remind students about the connection between the side length of a square and its area. Slides 14 and 15 provide two examples. Ask your students to complete the areas on their version of Copymaster One.
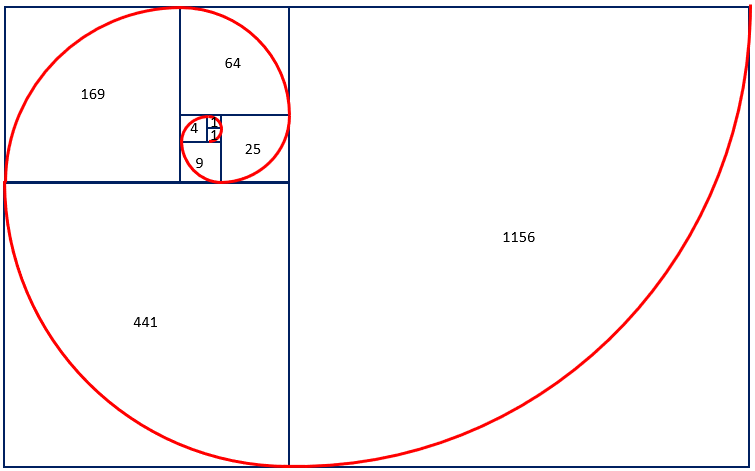
Why do the areas increase so rapidly?
Two things contribute to the rapid growth in area: the Fibonacci numbers themselves grow non-linearly (greater and greater differences), and those numbers being multiplied by themselves.
Use the following problem as an extension task (see Slide 16). Roam to ensure students have correctly completed the area model and understand how to identify the two Fibonacci numbers that are equal to the square of their place (n).
Here are the first few Fibonacci numbers:
| n | 1 | 2 | 3 | 4 | 5 | 6 | … |
| Fibonacci Number | 1 | 1 | 2 | 3 | 5 | 8 | … |
There are two Fibonacci numbers that are equal to the square of their place (n). Ask students to identify them.
You may need to illustrate some non-examples, such as:
The 6th Fibonacci number is 8. 6 x 6 = 36 so the sixth Fibonacci number is not six squared.
Both the first and twelfth Fibonacci numbers, 1 and 144, are the square of their place (n). 144 is the 12th Fibonacci number, and 12 x 12 = 144 (122 = 144).
Lesson Two
In the next two lessons students explore Fibonacci numbers in context and some of the patterns that exist with numbers in the sequence.
Introduce the Property Developers Problem using PowerPoint Two. For small numbers of sections in a row, it is easy to find all the possible layouts. For example, there are five layouts for a row of four sections (see Slide Five). Look for students to be systematic about finding all the possible layouts, so none are omitted. You might discuss symmetry when considering these layouts. Copymaster Two can be used by students to cut and paste the layouts in their workbooks or on a poster.
Let’s organise the data we have in a table. Call on students to fill in the cells for numbers of layouts.
| Number of sections | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Number of layouts | 1 | 2 | 3 | 5 | ? | ? | ? |
Does anything look familiar in the way the number of layouts is growing?
Students should notice that the pattern is the Fibonacci sequence.
Is there a way to check that the sequence works for any number of sections?
Students might suggest testing to see if the numbers of layouts for 5, 6, and 7 sections are Fibonacci numbers. This will give evidence that the pattern continues but not conclusive proof that it holds for any number of sections. You might use code to list all the layouts for 5, 6, and 7 sections.
5 sections (Begin with all that has S first, then move to D first)
- S, S, S, S, S.
- S, D, S, S.
- S, S, D, S.
- S, S, S, D.
- S, D, D.
- D, S, S, S.
- D, D, S.
- D, S, D.
6 Sections
- S, S, S, S, S, S.
- S, S, D, S, S.
- S, S, S, D, S.
- S, S, S, S, D.
- S, S, D, D.
- S, D, S, S, S.
- S, D, D, S.
- S, D, S, D.
- D, S, S, S, S.
- D, D, S, S.
- D, S, S, D, S.
- D, S, S, S, D.
- D, S, D, D.
Listing gets increasingly cumbersome with more sections. Support the attendance of your students as to why the Fibonacci numbers work in this case.
Slide Six has a systematic listing of layouts to four sections.
Can you use the listings for three, and four sections to work out how many different layouts are possible for five sections?
Let students discuss how they might predict the number of layouts for five sections. Slide Six animates how a systematic listing may be done.
What two ways can a layout start? (S or D)
Suppose we start a six-section layout with S. How can we find all the layouts that start with S? (Go to all the five section layouts since there are five sections to fill)
How can we find all the layouts that start with D? (Go to all the four section layout since there are four sections to fill)
How many six-section layouts are possible? (8 + 5 = 13)
Challenge your students, in small groups or pairs, to write down a convincing argument about how to find the number of different layouts for any number of sections. Look for the following:
- Do they say anything about the importance for the first section layouts?
- Do they specify how the two previous numbers of layouts help to create the number of layouts for a given number of sections? (e.g. To find the number of 10 section layouts go to the numbers of layouts for 8 and 9 sections)
- Do they explain why the two previous numbers of layouts are helpful?
Finish the lesson with the Assembly Problem which is similar but subtly different to the housing layout problem. If allocating 1 to a talker and 0 to a listener means the problem can be represented using strings of 1s and 0s. For three seats there are eight possible arrangements:
111, (three talkers)
110, 101, 011, (two talkers, one listener)
100, 010, 001, one talker, two listeners)
000 (three listeners)
The underlined arrangements are not allowed as there are two talkers together. There are five possible arrangements. Five is a Fibonacci number.
If there are four seats, then either a 1 or 0 can be used as the first seat. If 0 is used, then all five three seat arrangements can be ‘tacked on.’ If 1 is used, then only the three-seat arrangement starting with 0 can be used. There are three of those arrangements, 010, 001, and 000. In total 5 + 3 = 8 arrangements are possible with four seats. 3, 5 and 8 are Fibonacci numbers.
Lesson Three
In this lesson students explore some number patterns in the Fibonacci sequence. Use PowerPoint Three to drive the lesson. Begin with displaying the sequence using Slide One. Use mouse clicks to ask students to anticipate the next numbers in sequence.
Which of these Fibonacci numbers are even?
Is there a pattern to where they occur?
Continue the sequence to see if your predictions are correct.
A second row of Fibonacci numbers appear when you click the mouse. Students can check their sequence and confirm whether their prediction about when even numbers occur.
Can you explain why even numbers occur every third Fibonacci number?
Look for students to notice that the sequence goes:
Odd, odd, even, odd, odd, even, odd, odd, even, …
If two odd numbers occur consecutively the third number must be even since two odd numbers add to an even number. The next two numbers must be odd since an odd and even number make an odd sum.
Work through the second slide that shows a pattern with sets of four consecutive Fibonacci numbers. The example uses the numbers, 2, 3, 5, and 8.
2 + 8 = 10 and 10 ÷ 2 = 5. The sum is five, the third number in the set of four.
Is that just lucky, or does it happen all the time?
Let students investigate the pattern with other sets of four Fibonacci numbers. Here are some examples.
| Fibonacci numbers | Sum | Sum divided by two |
| 2, 3, 5, 8 | 2 + 8 = 10 | 10 ÷ 2 = 5 |
| 3, 5, 8, 13 | 3 + 13 = 16 | 16 ÷ 2 = 8 |
| 5, 8, 13, 21 | 5 + 21 = 26 | 26 ÷ 2 = 13 |
| 8, 13, 21, 34 | 8 + 34 = 42 | 42 ÷ 2 = 21 |
Challenge your students to explain why the pattern occurs. An informal proof is possible if students assign arbitrary names like a, and b to the first two numbers in the set of four.
If the set of four numbers start with a and b, what will the third and fourth numbers be? (a + b, and a + 2b, since the sequence is produced by adding consecutive terms to get the next)
What do we get if we add the first and last terms, a + (a + 2b)? The sum is 2a + 2b, or two lots of a + b, 2 (a + b).
If 2a + 2b is divided by two, what do you get? (a + b)
Which number of the set of four is that?
For students who find the use of variables difficult, you might try examples where the numbers are known. Cuisenaire rods or a stack of connecting cubes can act as a model. Slides 3 and 4 show how specific examples can be modelled to help students to see the structure of what occurs. They might then try to describe that structure.
Slide Five introduces a different pattern with four consecutive Fibonacci numbers. The example uses the numbers, 2, 3, 5, 8. 2 x 8 = 16 and 3 x 5 = 15. There is a difference of one.
Is there always a difference of one, no matter which four consecutive Fibonacci numbers you choose?
Let your students investigate whether the pattern works for other sets of our consecutive numbers. It does though the differences oscillate between positive and negative. Here are some examples:
| Fibonacci numbers | Products | Difference |
| 2, 3, 5, 8 | 2 x 8 = 16, 3 x 5 = 15 | -1 |
| 3, 5, 8, 13 | 3 x 13 = 39, 5 x 8 = 40 | +1 |
| 5, 8, 13, 21 | 5 x 21 = 105, 8 x 13 = 104 | -1 |
| 8, 13, 21, 34 | 8 x 34 = 272, 13 x 21 = 273 | +1 |
An explanation of why the pattern occurs will probably be beyond students at this level. Using a and b as the first two Fibonacci numbers and a + b, and a + 2b as the third and fourth requires algebra that is normally accessible at Level 6.
Lesson Four
Pattern One
In this lesson students investigate patterns that occur when Fibonacci numbers are squared. They may not be aware that they did this in Lesson One after constructing the Fibonacci spiral. Slide One of PowerPoint Four reminds them of this. Slides One and Two ask students to create a table of squares. You may need to discuss the notation, n is the ordinal number, Fn is the nth Fibonacci number, and (Fn)2 is the square of Fn. Copymaster Three can be used to speed this process up.
Look at the table. Try adding consecutive pairs of squares. For example, 4 and 9 are consecutive. 4 + 9 = 13.
What do you notice?
After a suitable period, bring the students back together to share their findings. They should notice that each sum is a Fibonacci number. Slide Three shows those results.
That’s interesting but can you be more specific? Let’s look more carefully.
Can you predict where the Fibonacci can be found?
Let’s take the sum of two squared and three squared. What Fibonacci number is thirteen? (Thirteen is the 7th Fibonacci number so it can be written as F7.)
It is the sum of squares of what two Fibonacci numbers? (22 + 32 = 13, and 2 is F3 and 3 is F4).
Write:
(F3)2 + (F4)2 = F7
What do you notice? Does this happen all the time?
Check some other examples.
Students should find several examples and conclude that “If you know the first Fibonacci number (Fn) then the sum of the two squares is Fn + Fn+1 (or F2n+1).”
You might write this as (Fn)2 + (Fn+1)2 = Fn+n+1. Proving the theorem takes algebra that is too complex for this level.
Pattern Two
Slides Four to Seven reintroduce the students to the arrangement of rectangles they used to create the Fibonacci spiral. They are asked to find the area of given rectangles. The area of the rectangles can be found by summing the areas of the squares within them.
Record the results in sequential order like this:
1 + 1 + 4 + 9 + 25 = 40
1 + 1 + 4 + 9 + 25 + 64 = 104
1 + 1 + 4 + 9 + 25 + 64 + 169 = 273
1 + 1 + 4 + 9 + 25 + 64 + 169 + 441 = 714
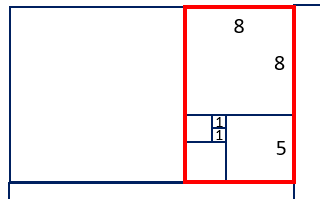
Return to Slides Eight and Nine of PowerPoint Four to pose the problem of finding side lengths. To do so students will have to work backwards from the areas to find the side lengths. Using the square root function on the calculator is one way to do this. For example, a square with area of 169 has side lengths of 13 since √169= 13. The side lengths of both rectangles are Fibonacci numbers since they are the sum of consecutive Fibonacci numbers.
For example, to find the side lengths of this rectangle students must first find the side lengths of the internal squares. Using √64= 8 and √25= 5 gives side lengths of 8 and 8 + 5 = 13. The area of the rectangle equals 8 x 13 = 104 square units.
The side lengths for the larger rectangle on Slide are 34 and 34 + 21 = 55, using √1156= 34 and √441= 21. Both 34 and 55 are Fibonacci numbers and the total area is 34 x 55 = 1870. Introduce this new information to the sequence you started previously:
1 + 1 + 4 + 9 + 25 = 40 = 5 x 8
1 + 1 + 4 + 9 + 25 + 64 = 104
1 + 1 + 4 + 9 + 25 + 64 + 169 = 273
1 + 1 + 4 + 9 + 25 + 64 + 169 + 441 = 714
1 + 1 + 4 + 9 + 25 + 64 + 169 + 441 + 1 156 = 1870 = 34 x 55
Ask students what they notice. Draw attention to both the addends and factors:
The squares add up to multiplication of Fibonacci numbers.
Copymaster Three requires students to complete the middle equations and add to the set above and below. The aim is for students to get more specific about what they notice. Completed patterns might look like this:
1 + 1 + 4 + 9 = 13 = 3 x 5
1 + 1 + 4 + 9 + 25 = 40 = 5 x 8
1 + 1 + 4 + 9 + 25 + 64 = 104 = 8 x 13
1 + 1 + 4 + 9 + 25 + 64 + 169 = 273 = 13 x 21
1 + 1 + 4 + 9 + 25 + 64 + 169 + 441 = 714 = 21 x 34
1 + 1 + 4 + 9 + 25 + 64 + 169 + 441 + 1 156 = 1 870 = 34 x 55
1 + 1 + 4 + 9 + 25 + 64 + 169 + 441 + 1 156 + 3025 = 4 895 = 55 x 89
Ask the students to attempt a rule for the pattern. You make need to support them with introducing series notation, such as:
(F1)2 + (F2)2 + (F3)2 +… + (Fn)2 to represent the sum of squares up to the square of the nth Fibonacci number. Specific examples might help the student to define the factors that combine to the sum.
12 + 12 + 22 + 32 + 52 + 82 = 104 = 8 x 13
12 + 12 + 22 + 32 + 52 + 82 + 132 + 212 = 714 = 21 x 34
The first factor is always Fn and the second factor is Fn+1, the next Fibonacci number after it. The theorem can be written as:
(F1)2 + (F2)2 + (F3)2 +… + (Fn)2 = Fn × F(n+1)
There are many other number patterns arising from the Fibonacci sequence.
Lesson Five
PowerPoint Five has a final problem set for the students to attempt independently or in small groups. The context of a telephone tree will be unfamiliar, but they should notice the Fibonacci sequence occurs as the number of new people are added with each minute. Continuing the tree will be very cumbersome so students should be encouraged to use the number pattern.
| Minutes | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
| New People | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | … |
Note that the sequence begins at minute zero, so the Fibonacci numbers are Fn+1, that is, one term along. Slide Four of PowerPoint Five has a continuation of the tree to support students who find drawing it difficult.
The answer is found by summing the Fibonacci numbers until 143 is reached or exceeded. That occurs when nine minutes elapse.
Discuss why the Fibonacci sequence is involved. Through drawing the tree students will see that the conditions for the sequence apply:
- It begins with 1, 1.
- Callers from both the previous layers of the tree contribute one new person.
Students might be interested that the sum of consecutive Fibonacci numbers to any n is always Fn+2 – 1. They might also be interested to note that all the rectangles in the spiral diagram are very similar, that is, they are scaled copies of one another. Slide Five shows some rectangles in sequence of size. Note that the sides are always consecutive Fibonacci numbers. The rectangles have similar side ratios, that is the long side divided by the short side. Slide Six has the beginnings of a table that students might continue. The ratio converges on a special number 1.61803398875, which is known as the golden ratio, and represented by the Greek letter phi, φ .
Slide Seven shows the Parthenon, in Athens, with a superimposed Fibonacci spiral. This could inspire students to investigate local or culturally-significant buildings and places that can demonstrate the Fibonacci spiral in the same manner. Some students might like to investigate the connection between Fibonacci numbers and the golden ratio further.
Dear family and whānau,
This week in class we have been investigating the Fibonacci sequence. Fibonacci numbers are a specific example of a sequence that is generated by rules dictating how to operate on the previous term to get the next term. The Fibonacci sequence is created using the recursive rule Fn = Fn-2 + Fn-1. That rule means that the nth Fibonacci number is the sum of the previous two Fibonacci numbers. This rule can be applied infinitely in a ‘recurring’ way. The sequence progresses as 1, 1, 2, 3, 5, 8, 13,..
Ask your child to tell you about some natural and human-made phenomena that reflect the Fibonacci sequence. You might even be able to find some examples of the sequence around your own house!