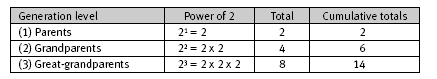This is a level 5 number link activity from the Figure It Out series. It relates to Stage 8 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (217 KB)
investigate powers of 2
FIO, Link, Number, Book Four, Family Trees, page 13
A calculator (optional)
Be aware when using this activity that family trees can get quite complicated if the students want to include relationships and second or third marriages. It is important not to make assumptions and to handle this activity with sensitivity.
An exponent indicates how many times a factor is repeated. For example, the small “5” in 25 is an exponent telling how often 2 is used as a factor in naming the product. Products expressed using exponents, for example, 25, are called powers. The fifth power of 2 is 25, which is 2 x 2 x 2 x 2 x 2 = 32. Exponents are used
to save time and space when writing out mathematical equations or large numbers.
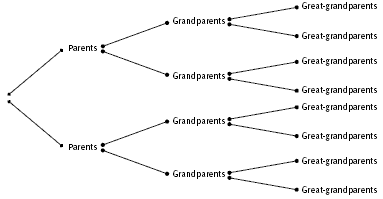
In question 1 of this activity, a tree diagram makes it easy to visualise how the number of grandparents progresses.
The students need to be aware that they must calculate a cumulative total of all three generations and not just the last in the sequence. To this end, they may find it useful to develop a table, such as the one below, as a problem-solving strategy for the more complex calculations required in questions 2–4.
For question 2, it is a matter of establishing the time span for one generation by dividing the years by the number of generations involved (75 ÷ 3). Then the students need to work out the number of generations altogether by dividing the total number of years by the time span for one generation (175 ÷ 25). Finally, they must extend the table created earlier so that they can include this seventh generation of grandparents.
After students working in small groups have attempted question 2, they should be able to share strategies with the class. You should also be able to ask: “How could you use your calculators with this investigation? What patterns have you seen?”
The total researched for each generation progresses in a doubling sequence that is easy to generate using the calculator constant: 2 x = = = = = = 128 . Note that there is always one more power of 2 than the number of = pressed because the 2 entered initially before the x needs to be included as a power. On a calculator with a yx key, you can enter 2 yx 7 = .
For the number researched, the cumulative total will always be 2 less than the total number of the next generation. The students can choose between keeping a cumulative frequency or waiting until they have all the generations listed and simply adding each generation, as outlined in the Answers.
The students can calculate question 3 by pressing the constant keys for multiplying by 2 and counting the sequence until they reach 1 000. Question 4 builds further on the strategies for questions 2 and 3. By now, the students will probably have realised the advantages of using a calculator. As an extension, some students could write and solve their own exponential stories. You should check that their stories make sense.
Answers to Activity
1. 14. (21 + 22 + 23)
2. a. 7
b. i. 128
ii. 27
c. 254
(21 + 22 + 23 + 24 + 25 + 26 + 27
= 2 + 4 + 8 + 16 + 32 + 64 + 128
= 254)
3. By the ninth generation (29 = 512), making a total of 1 022 people
4. a. 219 = 524 288
b. 1 048 574 (21 + 22 + 23 … + 219 or 524 288 x 2 – 2)