The purpose of this series of lessons is to develop understanding of the connection between division and fractions. In the unit both types of division, sharing and measurement, are explored to establish a need for fractions and to develop generalisations about division and fractions.
- Apply the understanding that fractions can be quotients (i.e. the result of division), e.g. 3 ÷ 5 = 3/5.
- Model and represent division problems with fractions that involve a measurement or sharing interpretation of division.
- Write and solve division problems that involve fractions.
Students need to understand and use the appropriate mathematical language for the numbers and symbols in division equations. Students need to understand and apply addend plus addend equals the sum for addition, and factor (multiplier) times factor (multiplicand) equals product for multiplication. Mathematical language for division allows for clear definition of the symbols, i.e., the meaning of those symbols, and allows for succinct expression of generalisations. In division, the dividend is partitioned by the divisor and this results in the quotient.
a (dividend) ÷ b (divisor) = c (quotient)
Division models the operation of equal partitioning in two different, but connected, types of situations. The first situation is sharing or partitive division, which often involves answering the question, “If a objects are equally shared among b parties, how many objects does each party get?” The second form of division is the measurement interpretation (sometimes referred to as quotative division). Here the number in the group, or size of each measure is known. That group or quantity becomes the unit of measure. The unknown in measurement division, is the number of those units that can be made from a given amount. This interpretation is often associated with repeated subtraction, as one way to solve this kind of problem is to keep removing the given equal groups (measures) from the whole amount, until nothing is left. Counting each repeated subtraction gives the solution to the question.
Measurement division situations are the easiest contexts for division by fractions. Problems with division by a fraction involve finding how units of a given (i.e. fractional size) ‘fit within’ another fraction quantity. For example, 1 1/2 ÷ 1/4 is interpreted as how many units of one quarter measure 1 1/2?
When students carry out the operation of division with whole numbers, their expectation is that the quotient will be smaller than the dividend, for example, 20 ÷ 2 = 10, and sometimes smaller than both the dividend and the divisor, for example, 20 ÷ 5 = 4. It is a conceptual shift for students to come to understand that when they are dividing a fraction by a fraction the quotient may be larger than both the dividend and the divisor, for example 1/2 ÷ 1/4 = 2.
There are many real-life occasions when we divide fractions by fractions, however, the fractions are frequently presented as decimals in measurement situations. For example, if you pay $15.00 for three quarters of a kilo of prime lamb and you want to know the price per kilo, that will involve you dividing a whole number by a fraction, i.e. 15 ÷ 3/4 =$20. Providing simple fractional problems in context, and asking students to consider and create their own contexts, is helpful to their connection of mathematics to the real world.
Links to the Number Framework
Stages 7 - 8
This unit supports and complements the learning activities in Book 7 Teaching Fractions, Decimals and Percentages.
Students can be supported through the learning opportunities in this unit by differentiating the nature and complexity of the tasks, and by adapting the contexts. Ways to support students include:
- providing a physical model, particularly of discrete objects (cubes, counters, etc.), and fraction strips so students can represent relationships and their thinking
- modelling how to represent division problems with fractions diagrammatically and with equations
- using mathematical vocabulary to identify common features in situations and the equations that represent those situations
- seeking generalisations of properties of operations from whole numbers, and applying the generalisations to fractions
- encouraging students to work collaboratively, and share their ideas.
Task can be varied in many ways including:
- Alter the complexity of the problems by simplifying the difficulty of the fractions and whole numbers that are used. Begin with fractions, such as halves, quarters, thirds, and fifths that students may be most familiar with.
- Provide access to physical representations so students can make sense of the actions in a situation, alongside using symbols.
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. Fractions can be applied to a wide variety of problem contexts, including making and sharing food or land from inheritance, constructing items, travelling distances, working with money, and sharing earnings. The concept of equal shares and measures is common in collaborative settings. Be conscious that fair sharing is not necessarily equal in whānau or community groups, e.g., bigger families might get more of a share. In te ao Māori, the sharing of food with visitors reflects manaakitanga. Hākari (feasts) are often included as a part of the celebrations of special events. In Samoan culture, food is an important part of events (e.g. weddings, funerals, church celebrations). Food, like other forms of wealth, is often shared evenly amongst the aiga (extended family). The learning in these sessions could be linked to learning about the tikanga (customs) of sharing food in the different cultures reflected in your classroom. In turn, this could foster greater connections and understanding amongst your learners.
Te reo Māori vocabulary terms such as hautau waetahi (unit fraction), hautua (fraction, part of a whole), whakarea (multiply), whakawehe (division, divide), toharoha (share, distribute), rautaki tohatoha ōrite (equal sharing strategy) and ōrite (equal) could be introduced in this unit and used throughout other mathematical learning.
- Unifix (or interlocking) cubes, or counters
- Strips of paper
- Scissors
- Calculators
- PowerPoint 1
- PowerPoint 2
- PowerPoint 3
- PowerPoint 4
- PowerPoint 5
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
Consider adapting this problem to suit the context of your class. It could be reframed as 84 students are taking part in Polyfest this year. They stand in 6 rows, with an equal number of students in each row. How many students stand in each row?
Note that most of the fractions in these teachers’ notes are displayed as typed text, meaning that the vinculum (the line between the numerator and the denominator) is diagonal rather than horizontal. When writing fractions on the board or in students’ books it is recommended that you use a horizontal vinculum.
Session 1
Activity 1
- Begin this session by showing this problem (Slide One of PowerPoint 1). These problems could be adapted to reflect the current interests and cultural makeup of your class (e.g. instead of a sports day focus, the context could be 180 students visiting the marae. 12 students can fit in the school van. How many trips need to be made to transport all students to the marae?)
On school sports day there are 180 students. They are put into teams of 12 students. How many teams are made? - Ask students to solve the problem without a calculator, then discuss their strategies with a partner. Encourage your students to record their work, to ease memory load and as a way to communicate their strategies.
- Ask students to record the problem equation on the chart (15 x 12 = 180 or 180 ÷ 12 = 15) and explain their strategy to the class. (for example: 10 x 12 = 120, 5 x 12 = 60 (halving), 120 + 60 = 180, and 10 + 5 = 15).
Note that many students are likely to use ‘build up’ strategies to find a solution. This strategy involves creating sets of 12 students until the total is exhausted. Their approach might be additive (repeated adding of twelves) or multiplicative (tracking the number of twelves as 180 is approached). - Ask: Is there a single operation that tells how many twelves can fit into 180?
- Model 180 ÷ 12 = 15 with a calculator. Discuss what the symbols in the equation mean, including the numbers (dividend (180), divisor (12), quotient (15)) and the signs (“measured in” (÷) and “is the same quantity as” (=)).
- Change the problem slightly to read (Slide Two of PowerPoint 1):
On school sports day there are 54 students. They are put into teams of 12 students. How many teams are made? - Let students work on their solution individually then in pairs. Share a few strategies as a whole class and record equations, such as:
[ ] x 12 = 54
54 ÷ 12 = [ ] - You might act out the problem using linking cubes as students. Discuss how to deal with the ‘leftover’ students. Students might suggest changing the number of students so an exact number of teams would work.
How many students should be in each team? (teams of six and nine students work evenly because 54 is divisible by both 6 and 9) - Solve 54 ÷ 12 = 4.5 using a calculator.
What does “point five” mean? (0.5 is the decimal for one half)
What does 4.5 tell us about the number of teams that can be made? (Four teams can be made with one half of a team remaining) - Use Side Three of PowerPoint 1 to show how six is one half of twelve. In this problem a team of 12 players is the unit of measurement.
4.5 can also be written as 4 ½. - Provide another problem for students to solve (Slide Four of PowerPoint 1):
For the Basketball tournament there are 62 students. They are put into teams of 8 students. How many teams are made?
Students might use the basic fact 8 x 8 = 64 to recognise that nearly 8 teams can be made. 7 x 8 = 56 indicates that 7 full teams can be made with 6 students left over.
What fraction of a team of 8 players is that? (6/8 or 3/4)
What will the calculator say when I use division? What equation shall I enter? (62 ÷ 8 = 7.75)
Recognising that 0.75 equals three quarters or six eighths involves equivalent fractions that will be accessible to many students. - Use Slide Five of PowerPoint 1 to model the fractions.
6/8 = 3/4 = 75/100 = 0.75
Activity 2
- Provide your students with Copymaster 1 that contains a series of group worthy problems about division with remainders. Encourage students to work in pairs or threes. Consider arranging these pairs to include more and less mathematically-confident students. Some students may benefit from working with the teacher on the first few problems. Provide calculators, whiteboards or scrap paper, and cubes/counters for students who need extra support.
- Roam the room and look for the following:
- Do students use addition or multiplication build-up strategies, or do they apply their knowledge of multiplication and division facts?
- Can students treat the team size as the unit of measure?
- Can students name the remainder as a fraction of the unit of measure?
- Do students connect the remainder, as a fraction, and the decimal they get from the calculator entry?
- After a suitable time, bring the class together to discuss their answers. Particular points to focus on are:
What question do you ask yourself to solve each problem?
For example, Question Two might be answered by “How many tens are in 93?”
How do you find the number of teams as quickly as possible?
How do you name the remainder as a fraction?
What kinds of numbers always have a remainder when divided into teams? (Primes) - Write on the class/group chart and pose this, or a similar question.
At the junior school sports day there are 86 students. If there are 7 in each group, how many groups are there? - Have students work in pairs. Tell them that their task is to solve the problem, discuss their strategy and write down how this problem is different from the first problem and suggest (show) how a younger child might solve the problem. Set a short time limit.
- Summarise the types of problems students have been solving.
What is the same about all the problems you have solved?
Aim to support students to understand that the situations have all involved measurement division. The team size is the unit in all problems, the divisor, and the total number of players is the dividend.
What does the answer, quotient, represent? (The number of teams)
Session Two
In this session students explore division as sharing into equal parts. They learn that sharing situations can also be answered using measurement division.
Activity 1
- Use Slide One of PowerPoint 2 to introduce this problem:
There are 84 students in Learning Environment Three.
The teacher wants to sort all students into six equal teams for the quiz.
How many students should be in each team?
Consider adapting this problem to suit the context of your class. It could be reframed as 84 students are taking part in Polyfest this year. They stand in 6 rows, with an equal number of students in each row. How many students stand in each row?
- Give the students time to attempt the problem independently then share their strategies in pairs. You might use Slide Two of PowerPoint 2, or use cubes, to illustrate strategies that students use.
As with measurement division students may use addition and multiplication build up strategies. For example, 6 x 5 = 30 (five students in each team), 6 x 10 = 60 (ten students in each team), 6 x 11 = 66, 6 x 12 = 72, …, 6 x 14 = 84 (14 students in each team)
How might the problem be solved in one operation? (84 ÷ 6 = 14)
Why would you ask yourself, “How many sixes are in 84?”
Look for students to explain that putting one person in each team makes a six. Finding out the number of sixes in 84 tells how many times one person can be allocated to each team. - Use Slide Three of PowerPoint 2 to introduce this problem:
32 students are in Room 8.
The teacher wants to share the students equally into five tug o’ war teams.
How many students will be in each team? - Ask students to attempt the problem in pairs. Look to see that they use the accessible fact, 6 x 5 = 30, to solve the problem. How do they deal with the remainder?
Students might suggest that three teams might have six players and the other two teams have seven players. Agree that equal teams are not possible.
What will the calculator say? - Invite predictions then ask students to key in
32 ÷ 5 = 6.4
What fraction is “point four?” (Students may know that 0.4 equals 2/5 or 4/10) - Use Slide Four of PowerPoint 2, or cubes, to enclose equals sets of six and connect them to the set rings. The remaining two people are two fifths of five, the number needed to give another person to each team.
- Pose another similar problem, such as:
Three working groups are made to weed the school vegetable garden.
There are 47 volunteers to do the work.
If all three gangs are equal, how many volunteers go into each gang? - Discuss strategies to solve the problem and the meaning of a calculator answer:
47 ÷ 3 = 15.66666666
Point six recurring (written as 0.6) equals two thirds, since two people remaining is two thirds of the number of volunteers needed for another single share.
Activity 2
- Ask students to work in pairs to write their own summary of the two kinds of division (measurement and equal sharing). Consider relating their problems to a shared context of learning from another curriculum area (e.g. your problems should be linked to what we have learnt about the Treaty of Waitangi).
Ask them to write a simple number problem for each kind of division, and write a division equation for each problem. As a class, you could develop sentence stems, starters, or guidelines to ensure everyone knows how to start writing their problem.
(NB. This task can be challenging. Focus on the language of sharing/each or number of groups). After an appropriate time, let students roam the room to get ideas from the work of other pairs. - Record a summary on the class chart. Use the words: dividend, divisor and quotient.
Show the meaning of each number and symbol in division equations, like this:
180 (dividend) ÷ 12 (divisor) = 15 (quotient).
= means “is the same quantity as”
÷ means “equally shared among” or “measured in units of” - Ask students to provide an example of a problem where the quotient has a remainder. For example, “22 players are put into teams of four. How many teams can be made?” written as 22 ÷ 4 = 5.5 or 22 ÷ 4 = 5 ½
- Reminded students about the meaning of the fraction in a quotient.
That fraction of the unit, or of a full share, remains.
Session 3
In this session, division as equal sharing is applied to problems with continuous whole, rather than the sets situations used in the previous two sessions. Students come to understand that quotients can sometimes be fractions, the result of division in which ones (wholes) are not sufficiently accurate.
- Use PowerPoint 3 to pose the following problems. These problems could be adapted to reflect a context that is more relevant to your learners (e.g. a tray of pani popo is shared between 3 people, how much does each person get?)
- 1 pizza shared between 3 people. How much does each person get?
Record the equation 1 ÷ 3 = 1/3 and discuss the meaning of the symbols. Note that the equal share is one third of a whole pizza. - 3 pizzas shared between 4 people. How much does each person get? (Slide Three of PowerPoint 3)
Let students create paper pizzas, or drawings, and share the pizzas physically. Some may cut the pizzas into halves first and give one half to each person. If they halve the remaining halves, they get quarters, so each person gets one half and one quarter of a whole pizza. In total each person gets one half and one quarter, or three quarters of a whole pizza. (See Slide Four)
Record a division equation for the operation, with emphasis on the meaning of the ‘divided by (÷)’ symbol as “equally shared among.”
3 ÷ 4 = 3/4 - 5 pizzas shared among two people. How much does each person get? (Slide Five of PowerPoint 3)
Notice that the number of pizzas is greater than the number of shares. That situation produces equal shares greater than one whole pizza, an important generalisation for students to make.
5 ÷ 2 = 5/2 = 2 ½
- 1 pizza shared between 3 people. How much does each person get?
- Slides Five and Six show two different ways to share five pizzas equally among two people. Usually students share out whole pizzas first then divide the remaining pizza among the two people. A generalised way to share equally involves cutting each pizza in half then giving each person one half from each pizza.
- Pose several other sharing problems for students to solve, such as:
- 2 pizzas shared between 5 people. How much does each person get?
- 4 pizzas shared between 3 people. How much does each person get?
- 5 pizzas shared between 8 people. How much does each person get?
- Ask students to work in pairs to create their solutions. Encourage students to draw diagrams and record equations to communicate their ideas. Some students will benefit from physically cutting paper circles to act out each problem. More advanced students could write new problems for their partner, or for other pairs of students.
- As students work, roam the room looking for the following:
- Do students create and correctly name the equal shares, using fractions?
- Do they exhaust all the pizza?
- Do they record division equations to model the situations?
- Do they notice the generalisation that a ÷ b = a/b?
- Gather the class to share solutions. Bring out the points above through discussion. It is particularly important that students recognise the symbolic generalisation. That generalisation is used extensively in algebra and whenever a fraction is converted to a decimal using a calculator, e.g. 3 ÷ 4 = 0.75.
- The Figure It Out series contains the following activity that can be used as independent activity for your students. A PDF is provided for the students to read and teacher notes are included.
Pizza split looks informally at division as non-commutative in a pizza sharing context, i.e., a ÷ b ≠ b ÷ a.
Session Four
- In this session students explore division when the dividend is a mixed number or fraction and the divisor is a whole number. They are encouraged to rename the mixed number as an improper fraction, e.g. 2 ¾ = 11/4. The problems involve sharing (partitive), and measurement (quotative) division.
Use Slide One of PowerPoint 4 to present this sharing (partitive) problem:
Problem dividend divisor quotient I have this much pizza (4½).
I want to share the pizza equally among the three people at my party.
How much pizza should each person get?
- Read the problem together.
What would the division equation for this problem look like? (4 ½ ÷ 3 = [ ])
Why is this problem difficult to solve? - Let students attempt to solve the problem in pairs. Encourage access to paper circles, and diagrams, so students can experiment and verify their answers. Some students may apply their learning from the previous lessons to find 4 ÷ 3 = 1 1/3, then divide the remaining one half among the three people. The result is 1 1/3 + 1/6 which equals 1 ½.
Could we look at the dividend (starting amount of pizza) in a way that makes the problem easier? - Slide Two of PowerPoint 4 shows the renaming of 4 ½ as 9/2. Sharing nine objects among three people is simple. Each person gets three objects.
How could we rewrite our equation? (9/2 ÷ 3 = 3/2)
Note that the dividend is nine halves, so the equal shares are three halves. - Complete the table to list the dividend, divisor, and quotient of the equation.
- Slide Three of PowerPoint 4 shows another problem where the dividend is a mixed number and divisor is a fraction. However, the situation involves measurement division.
I have 4 ½ metres of cloth.
Each bag is made from ¾ of one metre of cloth.
How many bags can I make? - Make strips of paper and scissors available to pairs of students.
Ask them to solve the problem and discuss their solutions with another pair.
Some students may approach it this way:
Students may realise that two units of three quarters equal one and one half. There are three units of one and one half in four and one half.
If we rename the divisor into quarters, how does that make the problem easier to solve?
How many quarters are in one? How many quarters are in 4 ½? (Slide Four of PowerPoint 4 shows the renaming of 4 ½ = 18/4.)
If I have 18 quarters, how many bags can I make? Each bag uses 3 quarters.
How can we write the problem as an equation? (18/4 ÷ 3/4 = 6) Record the discussion using the table used in problem one.
Problem dividend divisor quotient I have 4½ metres of cloth.
Each bag is made from ¾ of one metre of cloth.
How many bags can I make?
4 ½
or
18/43/4 6 - Make paper strips, fraction pieces and set collections (e.g. cubes or counters) available to the students. Distribute Copymaster 2, and discuss how to complete the task. Together complete the second example. Have students work in pairs to complete the empty sections, including writing their own fraction word problems.
- Have students pair share and mark answers.
Questions 6 and 7 require students to use the information provided. For example, Question 6 responses must involve 1 ½ ÷ 6 = ¼ . Sharing division provides the easiest contexts, e.g. “Jim has one, and one half hours to wash six cars. What fraction of an hour should he spend on each car?” Measurement division is more complex, “It takes Jim six hours to paint the fence. What fraction of the fence can he paint in one, and one half hours?”
Question 7 requires students to apply inverse thinking to identify the dividend. Since 8 x 2/5 = 16/5 = 3 1/5 the division problem must be 3 1/5 ÷ 2/5 = 8. Problems will probably involve measurement, e.g. “Kaylene has three and one fifth metres of ribbon. It takes two fifths of one metre to tie each bouquet. How many bouquets can Kaylene tie?
Session Five
In this session students explore division where the dividend is a whole number and the divisor is a fraction, e.g. 1 ÷ 2/5 = 5/2 = 2 ½. Fraction strips (See Copymaster 3) are used as the physical representation since length is the simplest attribute for students to use. The problems involve measurement division since a fractional number of shares makes no sense. For example, 1 ÷ 2/5 means “How many quantities of two fifths equal one?”
- Begin with Slide One of PowerPoint 5. You may like to use an online manipulative tool for fraction strips. There are many available.
Jamal cycles two thirds of a kilometre in one minute.
How much time does he take to cycle one kilometre?
Animating the slide allows two thirds to be shown as a unit. Treating a non-unit fraction as a single unit is a major conceptual challenge for students.
Possible answers might be:
“One” (Disregarding the extra part)
“Not quite two” (Accepting the extra part but not being precise)
“One and a bit”
The challenge is to name the ‘bit’ in terms of the divisor of two thirds. There are one and one half lots of two thirds in one. Jamal takes one and one half minutes to ride one kilometre.
What is one and one half as a fraction? (1 ½ = 3/2)
How can the operation be written as an equation? (1 ÷ 2/3 = 3/2) - Use Slide Two of PowerPoint 5.
Arohia cycles two fifths of a kilometre in one minute.
How long does she take to cycle one kilometre?
Students should establish that two, and one half lengths of two fifths make one. Record the equation as:
1 ÷ 2/5 = 5/2 = 2 ½
Why is the answer five halves? (There are five fifths in one, and two fifths are used each time. The answer should be the same as the answer to
5 ÷ 2 = 5/2 = 2 ½ - Use Slide Three of PowerPoint 5.
Mere cycles three eighths of a kilometre in one minute.
How long does she take to cycle one kilometre?
What is this problem as division? 1 ÷ 3/8 = [ ]
What is the answer? 1 ÷ 3/8 = 8 ÷ 3 = 8/3
Mere takes two and two thirds minutes to cycle one kilometre. - Use Slide Four to show the answers so far.
Is there a pattern?
Students should notice the reciprocal (upside down) relationship between the divisor and the quotient.
For example, the numerator of 3 in the divisor results in a denominator of 3 in the quotient, and the denominator of 8 results in a numerator of 8 in the quotient.
1 ÷ 3/8 = 8 ÷ 3 = 8/3 - Provide the students with Copymaster 4 to work from in pairs. Students may need access to fraction strips in physical, or online virtual form, to solve the problems.
- Roam the room as students work. Look for the following:
- Do your students identify the divisor as a unit of measurement?
- Can they draw an appropriate strip diagram to model each problem?
- Are they able to express the number of times the unit fits into one (whole) using fractions?
- Do they apply the generalisation that 1 ÷ a/b = b/a ?
- Bring the class together to share solutions. Interesting points to raise are:
- Question Six:
The diagram looks like this: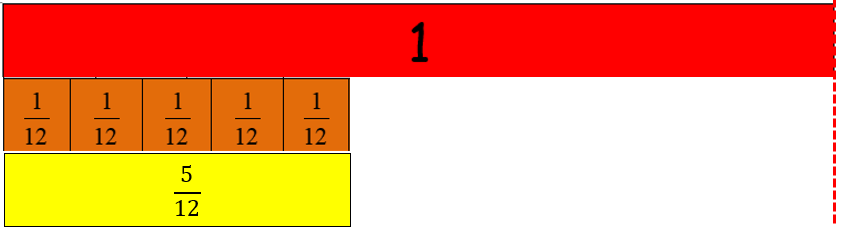
How can we figure out how many times a unit of five twelfths fits into one? (12 ÷ 5 = 12/5) - Questions Five and Seven:
These are inverse problems, that is 1 ÷ a/b = 7/3 and 1 ÷ a/b = 5/2 though the algebra is not necessary.
Connect these problems to whole number division, e.g. 15 ÷ [ ] = 5. To solve the whole number problem students might choose [ ] x 5 = 15 or 15 ÷ 5 = [ ]. So, 1 ÷ 7/3 = 3/7 gives the answer to Question Five and 1 ÷ 5/2 = 2/5 gives the answer to Question Seven.
- Question Six:
- You may like to finish the unit by asking students to create a poster or a journal entry about the connection between division and fractions. You might create a class poster for display in the mathematics area of your classroom.
Dear parents and whānau,
We have been exploring the connection between division and fractions in class.
You might enjoy solving these two problems together to see what they have been learning.
Problem One: Four people equally share three doughnuts. How much of one doughnut does each person get?
Problem Two: If each person needs three eighths of a big pizza, how many people can be fed with one and one half pizzas?