The purpose of this activity is to engage students in finding a pattern from multiplying dimensions and to generalise this pattern with a rule.
This activity assumes the students have experience in the following areas:
- Use side lengths to calculate areas of rectangles and triangles.
- Scale figures by a given factor and understand the effect of the transformation.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
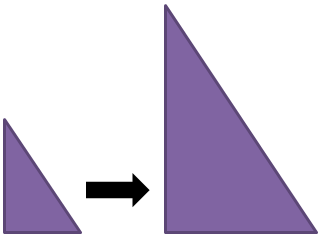
If a triangle is enlarged by scale factor 2, what is its increase in area?
What if the scale factor was 3?
What if the scale factor was n?
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- Do I understand the situation? (Students may need support to understand the meaning of enlargement, especially the use of scale factor. The scale factor is the multiplier that maps side lengths in the original figure to corresponding side lengths in the image.)
- Will it matter which triangles I try? (Equilateral, right-angled, scalene, etc.) Will that make a difference to what happens to area?
- Can I visualise what the change in area might be for a scale factor of 2, using the picture? How will my image change for a scale factor of 3?
- What will a solution look like? (A rule for change in area of a triangle as scale factor changes.)
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What strategies can I use to get started? (Drawing on squared paper is a good first step to generate examples.)
- What examples will be best to try first?
- What mathematics am I going to need? (Finding the area of triangles is required.)
- Do I expect there to be a pattern?
- How will I record to make the pattern visible?
- What tools (digital or physical) could help my investigation?
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Have I tried many examples of triangles with different scale factors?
- How can I be sure my calculations of area were correct?
- Did I record my data in an organised way?
- Have I got enough examples? What other examples would be useful?
- Do I see a pattern? How might I describe the pattern I see?
- Could I draw diagrams of triangles to show confirm the pattern? (Partitioning the image triangle into units of the original triangle is helpful.)
- Do I have a rule connecting scale factor and area?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is my solution?
- Is my working clear for someone else to follow?
- How would I convince someone else I am correct?
- What is the best way to express my solution?
- Are there examples that my rule doesn’t work for?
- Could I use algebra to prove that my rule always holds?
- What connections can I see to other situations, why would this be? (Does varying the original image effect the change in area?)
- What mathematics have I learned? What mathematics do I need to learn more about?
Examples of work
Work sample 1
The student finds the areas of an original triangle and an enlarged triangle and relates the scale factor to the increased area of the enlarged triangle. The student works with natural (counting) numbers for scale factors.
Click on the image to enlarge it. Click again to close. 
Work sample 2
The student finds the areas of an original triangle and an enlarged triangle, and generalises the increase in area, in terms of the scale factor. They use algebra to generalise the effect on area of varying the scale factor.

