The purpose of this activity is to support students in applying linear relationships to find unknown values of the explanatory variable, the x-value or value of n, when given the value of the response variable, the y-value or nth term. Students are not expected to master solving linear equations, though the strategy should be introduced in context.
- Squared paper
- PowerPoint (in paper form or displayed on a shared screen)
- Show students slide 1 of the PowerPoint.
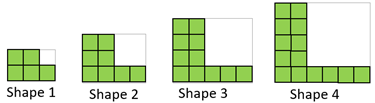
Find a general rule for this growing pattern.
Can you write the rule using algebra?
Can you graph the relation between Shape Number and number of squares?
Let students find a general rule individually or in small groups. You might organise these groups to encourage tuakana-teina.
- Gather the students and discuss their strategies. Look for the following:
- Using a table of values to find a general (function) rule.
| Shape Number | 1 | 2 | 3 | 4 | 5 | ... | n |
| Number of squares | 5 | 8 | 11 | 14 | 17 | ... | 3n+2 |
| Change in number of squares | +3 | +3 | +3 | +3 |
- Using schematic diagrams to structure the pattern (see slide 2).
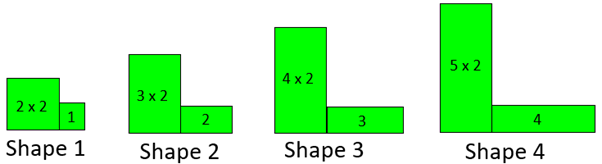
Look at what changes and what stays constant as the pattern grows.
The general rule for the nth term must have □ x 2 + ∆
□ is always one more that the Shape Number (n + 1).
∆ is always the Shape Number (n).
The general rule is (n + 1) x 2 + n that can be written as 2(n + 1) + n and rearranged as 3n + 2.
The general rule can be written as a linear equation. The first step is to assign letters to represent the variables. A mathematician would write something like this:
Let n be the Shape Number and s be the Number of squares.
They would write s = 3n + 2. That is an equation since it contains an equal sign.
- Challenge students with this problem:
The pattern grows until it takes 92 squares to make the shape.
What is the Shape Number, n?
Let students work on the problem in appropriate groupings. Some students might benefit from working independently, whilst others may need further teacher support.
After a suitable time, gather the students to share their strategies. One possible strategy is continuing the table of values by repeatedly adding three until 92 squares is reached. While this recursive (one after the other) strategy works, it is inefficient. Emphasise the use of more efficient strategies (mentioned above).
Shape Number 1 2 3 4 5 … 30 Number of squares 5 8 11 14 17 … 92 Change in number of squares +3 +3 +3 +3 - Extend the graph using digital graphing technology, such as Desmos.
Reading the order pair as (30, 92) shows that Shape Number 30 is made of 92 squares.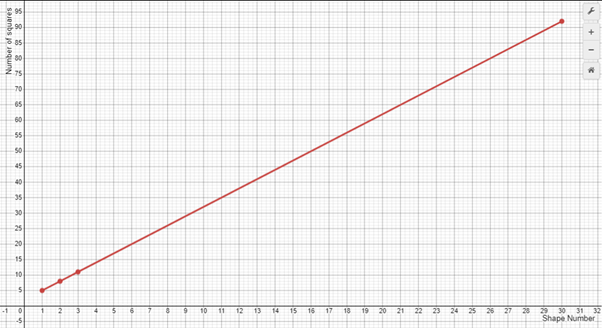
- Use algebra by setting the number of squares to 92 in the equation.
92=3n+2
Find the value for n that makes the equation true. Guess and improve methods might be used, or the same operation might be applied to both sides. For example:
- 90=3n (Subtracting two off both sides)
- 30=n (Dividing both sides by three)
To provide more support for students in solving simple linear equations use the Visual Linear Algebra Tools.
- Provide further examples for which students need to develop a general rule and apply that rule to find an unknown Shape Number, given the number of squares.
- Slide 3 of the PowerPoint has a decreasing ‘growth’ pattern.
How many squares are in the L shape to start? (192. This is an interesting problem in itself)
Let’s call that shape Zero.
Animate the slide. Small L shapes are removed at each stage automatically to form a new shape each time.
What Shape Number will have zero squares?
Students might form the general rule for the nth term as 192 – 3n which gives the equation s = 192 – n. They may use tabular, graphic, or algebraic strategies to find the solution, n = 64. Graphically the solution look like this: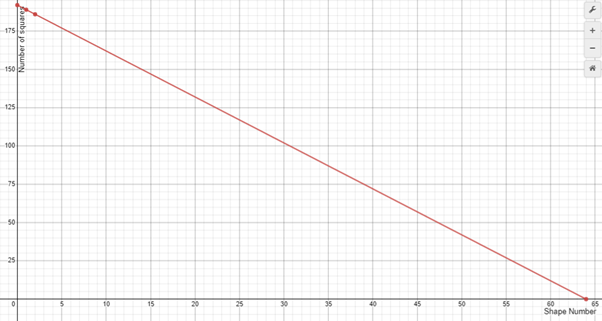
Algebraically the problem can be solved as:
0=192-3n
3n=192
n=64
- Revisit the pattern of the growing person (see slide 4).
What is the general rule for this pattern?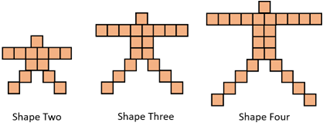
Together, construct a table of values.
Shape number 1 2 3 4 5 6 7 8 9 10 Number of squares 7 13 19 25 31 37 43 49 55 61 Change in number of squares +6 +6 +6 +6 +6 +6 +6 +6 +6
Students may recall that the number of squares is always six times the Shape Number plus one. The nth term can be written as 6n + 1. This gives the equation y=6x+1.
If 91 squares were used to make a shape in this pattern, what Shape Number was it?
Look for students to use graphical and algebraic strategies to find the solution to 91=6x+1 ? (Shape number equals 15).
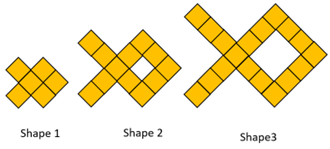
- Use the horse pattern on slide 5.
What is the equation for this growing pattern?
General rules may vary since only one shape in the pattern is given.
However, settle on y=4x+1, where x is the Shape Number and y is the number of squares.
If 413 squares were used to make a shape in this pattern, what was the Shape Number?
Look for students to solve y=4x+1, to find x = 103.
Use the fish pattern on slide 6.
Write an equation for this relation, using x for the Shape Number and y for the number of squares. (y = 6n + 2).
320 squares were used to make a fish shape in this pattern. What was the pattern number?
Look for students to solve 320=6n+2.
Next steps
- Provide students with opportunities to use digital platforms, such as Desmos, to predict the equation of a given linear graph.
Start with minor variations of y = x , such as y = 2x , and y = 5x , to explore the effect of changing the coefficient of x (Changes the steepness/slope).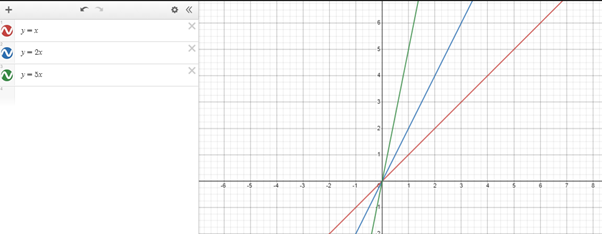
- Explore keeping slope the same but changing the point where the graph crosses y-axis. Start with minor variations like y = 2x , y = 2x+1 , y = 2x+5.
Look for students to anticipate the graph of a linear equation, such as y = 0.5x-2.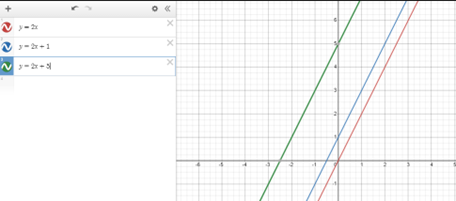
- Extend the range of relations to include patterns that do not linear relations. Pay particular attention to simple exponential growth patterns. Use technology to calculate the next terms.
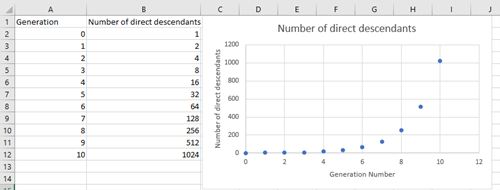
For example, here is a diagram of direct ancestors (parents, grandparents) in a whakapapa.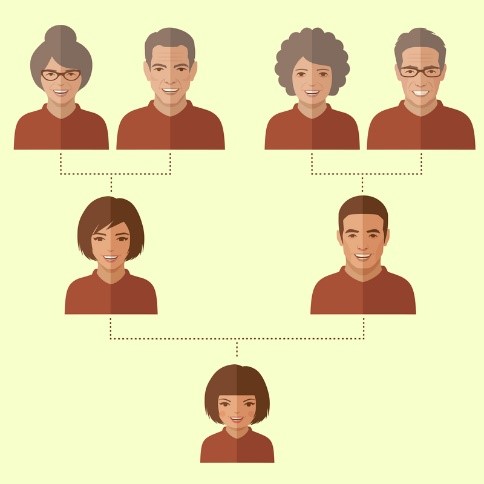
How many direct ancestors do you have if you go back ten generations?
- Look for students to notice that the number of ancestors doubles with each generation.
- Use a spreadsheet to calculate the values and graph the relation. Students are not expected to write exponential equations.