New Zealand Curriculum: Level 2-3
Learning Progression Frameworks: Measurement sense, Signpost 4 to Signpost 5
Target students
These activities are intended for students who can apply their understanding of whole number place value with two-, and possibly three- digit numbers. By the beginning of Level 3 students are expected to use scales, such as a ruler, to measure the length of objects using appropriate metric units. They are also expected to solve problems in which metric units and combined or partitioned. Students are developing an understanding of choosing an appropriate degree of precision for a measuring task. They are also learning to estimate measures where the divisions on the scale do not align with the object being measured.
The following diagnostic questions indicate students’ understanding of, and ability to use, linear scales to measure length. (show diagnostic questions)
The questions should be presented orally and in a written form so that the student can refer to them. The questions have been posed using realistic measurement contexts though the arrangements of the ruler/s is deliberately aimed at assessing students’ understanding of scales. You may prefer to use authentic tasks, measuring objects in your own classroom.
- How long is the envelope?
How do you know? Write down the measurement.

Signs of fluency and understanding:
Recognises the units of length as centimetres, correctly reads 22cm from the ruler, and writes the measure as 22cm or 22 centimetres.
What to notice if they don’t solve the problem fluently:
Sees that the measure is 22 but does not identify the unit as centimetres. This indicates a lack of familiarity with metric units for length.
Names the measure as 22 centimetres but does not record it as 22cm. This indicates lack of experience with recording metric measures of length.
Supporting activity:
Measuring in centimetres with a ruler
- How long is the pen?
How do you know? Write down the measurement.
 |
|
Signs of fluency and understanding:
Recognises that the baseline is at 3cm rather than zero and adjusts the measure accordingly, either by imaging the pen shifting to the left by 3cm or finding 16 – 3 = 13cm.
Explains that the baseline is not zero, so the endpoint measure needs to be adjusted.
Records the measurement as 13cm.
What to notice if they don’t solve the problem fluently:
Reads the measurement as 16cm. This indicates that the student has not noticed the non-zero baseline or considering the endpoint of the object as the indicator of length, irrespective of the position of the object.
Sees that the measure is 13 but unsure of the unit as centimetres. This indicates a lack of familiarity with metric units for length.
Names the measure as 13 centimetres but does not record the measure as 16cm. This indicates a lack of experience with recording metric measures of length.
Supporting activity:
Using the baseline
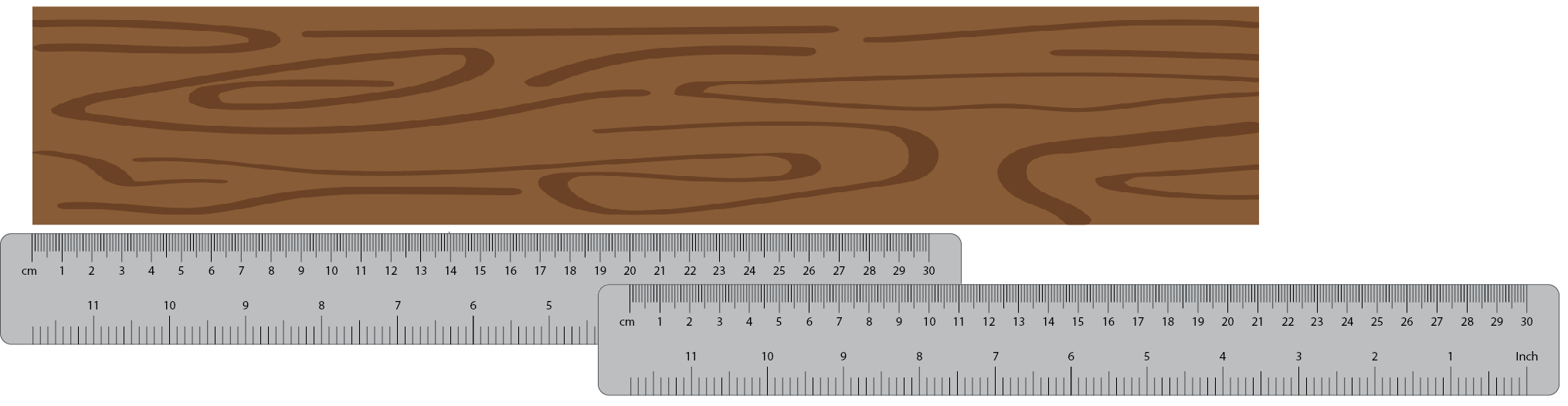
- How long is the wooden strip?
How do you know? Record the measurement.
Signs of fluency and understanding:
Recognises that the two measurements can be combined to find the overall length of the wooden strip. Calculates 20 + 21 = 41cm and records the measure correctly. This shows the student understands that measurements are iterations (copies) of a unit and can be treated just like sets are in any calculation context.
What to notice if they don’t solve the problem fluently:
Reads the endpoint of the object as the total length of 21 cm. This indicates that the student does not notice the two components of length or is unaware that two measures can be combined.
Supporting activity:
Joining measures of length
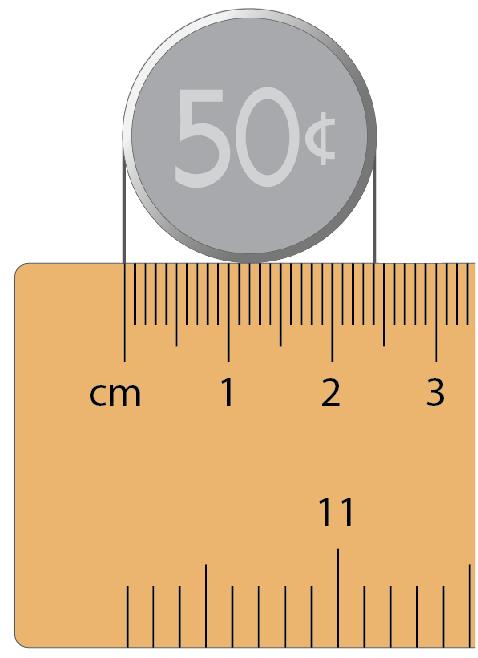
- How wide is the coin?
How do you know? Record the measurement.
Signs of fluency and understanding:
Recognises that the whole number units are not accurate enough and expresses the width of the coin either in millimetres, 24 mm, or as a decimal amount of centimetres, 2.4 cm.
What to notice if they don’t solve the problem fluently:
Uses whole numbers of units to measure the width, most likely 2cm but possibly 3cm. This indicates that the student is unaware of partitioning of centimetres into ten parts to create millimetres.
Sees that 24 smaller marks measure the width but cannot express the measure using millimetres or decimals of centimetres. This indicates the student is unfamiliar with tenths of centimetres as millimetres.
Supporting activity:
Choosing units of length for greater precision
How long is the pencil?
How do you know? Record the measurement.

Signs of fluency and understanding:
Estimates the length of the pencil in either centimetres or millimetres using one of two processes:
- Equally partitions the length between zero and 20 centimetres, possibly by halving then finding quarters. Concludes that the pencil in about 15cm or 150mm long.
- Uses the space between 20 and 21cm to find a unit of 1cm. Iterates (copies) the unit with no gaps or overlaps, to estimate the length. The student may build up from zero or come back from 20cm. Estimate will be about 15-16cm or 150-160mm. The student might use a fingernail as a unit as they iterate.
What to notice if they don’t solve the problem fluently:
Estimates with little accuracy, far from 15-16cm or 150-160mm. This indicates a lack of experience with estimating by either partitioning an interval or iterating a unit. Shows uncertainty about which unit to use, centimetres or millimetres. This may result in estimates such as 14 or 18 millimetres and indicates that the student lacks a ‘feel’ for the size of the units and/or a sense of benchmarks such as 10cm.
Supporting activity:
Using scales
Teaching activities

 |
| 

