New Zealand Curriculum: Level 4
Learning Progression Frameworks: Patterns and relationships, Signpost 5 to Signpost 6
Target students
These activities are intended for students who use a broad range of strategies for addition, subtraction, and multiplication of whole numbers. They should have knowledge of most basic facts for addition, subtraction, and multiplication and have experience with making predictions about further members of spatial growth patterns (see Finding and expressing relationships at Level 3)
The following diagnostic questions indicate students’ understanding of, and ability to identify which features of a growth pattern change and which remain constant. The questions also explore students’ knowledge of representing growth patterns as word rules, tables, graphs, and equations. Allow access to pencils, paper and a calculator (for checking answers) if needed. (show diagnostic questions)
The questions should be presented orally and in a written form so that the student can refer to them. The questions have been posed using a square tiles context but can be changed to other contexts that are engaging to your students, such as tukutuku panels or tapa cloth.
What does the 20th shape in this pattern look like?
How many squares are in the 20th shape?
Signs of fluency and understanding:
Structures the 20th shape by seeing what features change and what features stay constant as the pattern progresses. Explains that the twentieth shape will have 22 squares on each side of a square with the bottom right square missing. May use various methods to calculate the number of squares, including:- Drawing a schematic diagram (rather than individual squares) and calculating the edge lengths as 22 + 21 + 20 + 20 = 83.
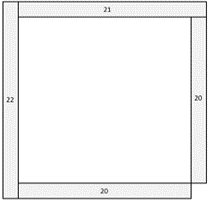
- Imagining the square is complete and subtracting one square and calculating the edge lengths as (2 x 22) + (2 x20) – 1 = 83.
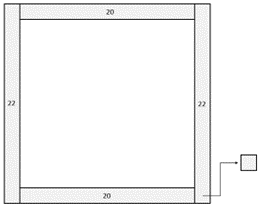
Using a table of values to generate a function rule:
Shape number 1 2 3 4 ... n Number of squares 7 11 15 19 ... 4n+3
Explains the rule as “multiply the shape number by four and add three” rather than using algebraic symbols.
What to notice if they don’t solve the problem fluently:
Begins a table of values, as above, but uses additive strategies to extend the table values, i.e., add four each time. Use questioning (for example “Is there a way to work out how many squares shape 20 has without adding four each time?”) to prompt further thinking. This strategy indicates that the student prefers to use recursive (one after the other) rules. They should be given support to look for function rules that connect the variables (shape number and number of squares in this pattern).
Attempts to draw shape 20 by attending to some structural features. For example, the student might draw a square figure with an incorrect number of squares on each side or draw a rectangular figure that is not square. This indicates that the student looks for organisation (structure) in the pattern without identifying all the important features. The student needs support in identifying the relevant features and connecting the shape number to those features.
Supporting activity:
Creating function rules
- Drawing a schematic diagram (rather than individual squares) and calculating the edge lengths as 22 + 21 + 20 + 20 = 83.
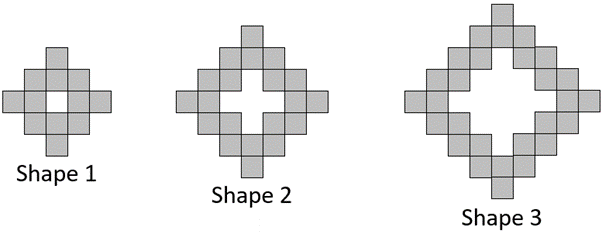
Here is the third shape in a growing pattern.
What do you notice about the way the shape is made?
How many squares make up Shape 20 in the pattern? Explain how you know.
Signs of fluency and understanding:
Structures the third shape as having a central square and four arms of three squares. Transfers the structure to imaging the 20th shape having a central square and arms of 20 squares. Calculates (4 x 20) + 4 = 84.
Note that there are many ways to imagine the pattern growing, such as only adding to three arms or two arms. Students may develop equally correct growth scenarios. There are also other ways to structure shape 3 such as having a horizontal arm of seven squares and two vertical arms of three squares each. Transferring that structure to shape 20 leads to a total of 41 + 2 x 20 = 81 squares.
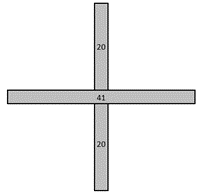
What to notice if they don’t solve the problem fluently:
Draw the previous and next shape in the pattern to get a sense of how it grows.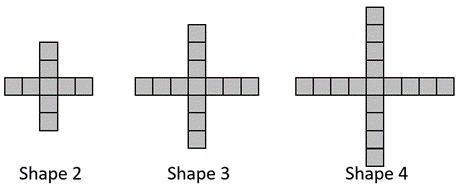
May create a table of values and extend the table to find the total number of squares in shape 20, using the additive pattern of adding four each time.Shape Number 1 2 3 4 5 … 20 Number of Squares 5 9 13 17 21 … 81 Look out for the ratio error of finding the number of squares for shape 5 and multiplying the answer by four, 4 x 21 = 84.
These strategies suggest that the student needs experience in noticing structure in a single shape in a pattern and applying that structure to create function rules.
Supporting activity:
Reasoning from one shape
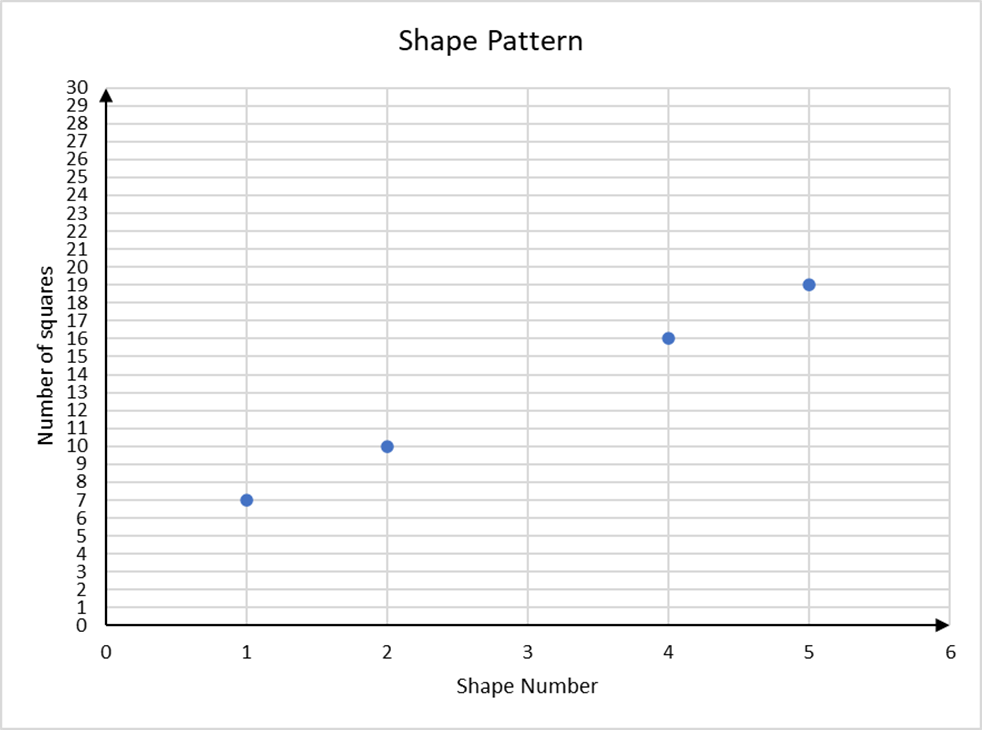
- Here is a graph of a growing pattern of shapes.
Draw points to show the number of squares that make up shapes 3 and 6.
What patterns do you see in the graph?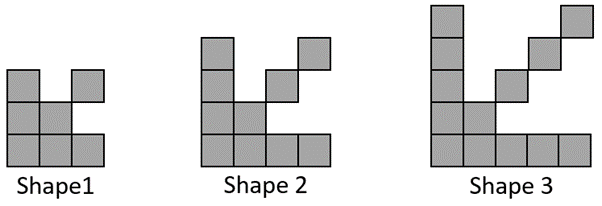
Signs of fluency and understanding:
Coordinates the values of shape number and number of squares as an ordered pair and represents (3, 13) and (6, 22) as points on the number plane.
Explains the meaning of each point in terms of shape number and number of squares.
Notices that the points on the graph lie on a line. It is not necessary for the students to describe the reason the points are linear, or the slope and intercept of the line.
What to notice if they don’t solve the problem fluently:
The student may be unable to represent the ordered pairs (3, 13) and (6, 22) as points on the graph. This suggests that the student needs experience with graphing relations on a number plane.
Attempts to locate the points but is unclear of which number, shape or number of squares, relates to horizontal distance and which number relates to vertical distance. This indicates that the student needs experience with identifying the independent (explanatory) variable and the dependent (response) variable in relations, and graphing ordered pairs as horizontal and vertical movements.
Supporting activity:
Graphing relations
Leeana, Cody, and Prakesh create their own rules for the number of squares of any shape in the pattern.
They use n to represent the shape number.
Leeana pictures the pattern like this and writes her rule as (n + 1) + 2n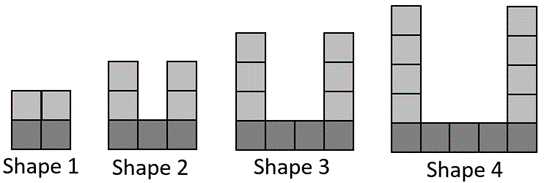
Write Cody and Prakesh’s rules as algebraic expressions.
Cody pictures the pattern like this: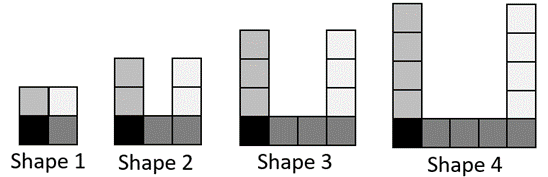
Prakesh pictures the pattern like this:
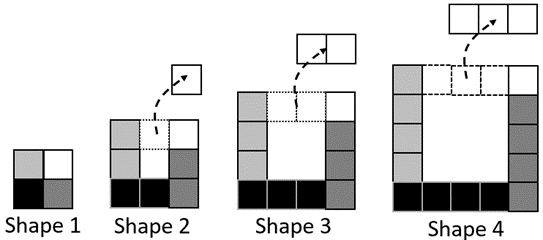
Signs of fluency and understanding:
Interprets the diagrams by connecting the shape number to the units of squares.
They may do so by reasoning from one shape in the pattern.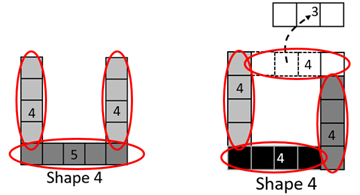
Use algebraic conventions to express the general rules algebraically. These expressions might take the following different forms:
n+1+2n 4n-(n-1)
Look for students to express the number one more or less than n as n+1 and n-1, respectively, and correctly record n times a number, e.g. 4n for “n multiplied by four.”
What to notice if they don’t solve the problem fluently:
The student may have difficulty interpreting how Cody and Prakesh structured the spatial patterns. Discuss the shading of blocks of squares then ask the student to reattempt the question.
Identifies the key parts of the diagram for each person’s rule but is unable to relate the size of the parts to the shape number to develop a rule for the nth pattern. This suggests that the student needs support to express the value of one variable in terms of another which may involve identifying the nature of relationship and/or learning the conventions for expressing relationships algebraically.
Supporting activity:
Expressing general rules
If you use 100 squares, what is the largest numbered shape in this pattern you can make?
Let students have access to a calculator, or a computer spreadsheet if they are familiar with using one.
Signs of fluency and understanding:
Establishes that the general rule connecting shape number, n, with the number of squares is 8n+4.
Works backwards from the general rule, in either of two ways:
1. Informally, such as subtracting 4 from 100 the dividing 96 by 8 to get 12 as the shape number. Some students may use trial and error methods which are not as efficient, that is, try different values for n to see which value gives 100.
2. Formally using algebraic manipulation, as follows:
8n+4=100
8n = 96
n=12
If familiar with using a spreadsheet, the student might extend a table or values or extrapolate from a graph to find the missing value.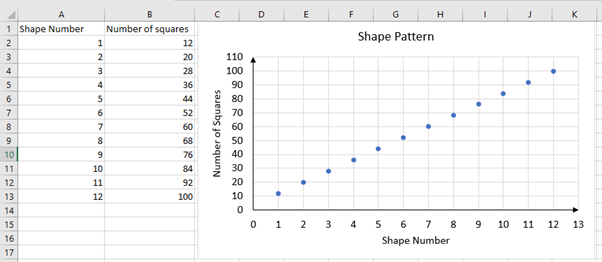
What to notice if they don’t solve the problem fluently:
The student may have difficulty finding a general rule connecting the shape number with the number of squares. This indicates they need more experience in developing general rules for spatial growing patterns.
Creates a table of values for the first few shapes and uses additive thinking until a total of 100 squares is found.Shape number 1 2 3 4 5 6 7 8 9 10 11 12 Number of Squares 12 20 28 36 44 52 60 68 76 84 92 100 +8 +8 +8 +8 +8 +8 +8 +8 +8 +8 +8 This suggests that the student needs support to develop function rules from a table of values. A function rule connects the numbers in each ordered pair, so works from the shape number to the number of squares, rather than adding on horizontally to find the next number of squares.
Supporting activity:
Working backwards