Finding and expressing relationships (Level 3)

The questions should be presented orally and in a written form so that the student can refer to them. The questions have been posed using a square tiles context but can be changed to other contexts that are engaging to your students, such as tukutuku panels or tapa cloth.

1. Draw the shape that comes next in this pattern.  
   How many squares is it made up of? How do you know?  
     
   
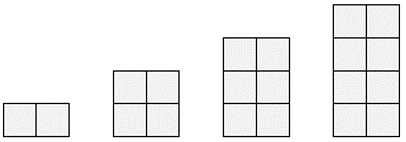
   Signs of fluency and understanding:  
   Attends to the constant width of each tower and to the change of one layer with each progression. Draws a 2 x 5 tower and says the number of square equals ten, either by subitizing (recognising a tens frame), by skip counting, addition of 5 + 5, or with multiplication.  
   
   What to notice if they don’t solve the problem fluently:  
   Unable to create any drawing, or draws a tower of squares that lacks the structure of the pattern (for example, the tower may be arranged in an array but is not 2 x 5). This indicates that the student needs experience noticing what changes and what stays the same in growing patterns.  
   
   Supporting activity:  
   Next shape  
    

2. Here is a pattern. How many squares are in Shape 10?  
   Use a calculator if you need to. Explain your answer.  
     
   
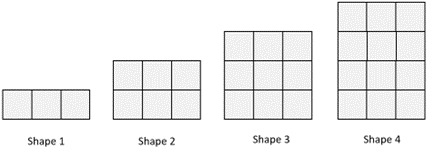
   Signs of fluency and understanding:  
   Recognises that the width of the tower stays constant, and the tower grows by one layer each time. Identifies that the shape number gives the number of layers in each tower, and recognises that therefore the tenth tower will be made up of ten layers of three squares. Calculates 10 x 3 = 30 squares. This strategy shows functional thinking, by finding a relationship between variables.  
   Possibly creates a table of values:

   Shape Number	1	2	3	4	5	6	7	8	9	10
   Number of Squares	3	6	9	12	15					30

   Notices that the pattern grows by three and repeatedly adds three until the tenths shape is found. This is an additive  strategy based on recursion (one after the other) thinking.  
   
   What to notice if they don’t solve the problem fluently:  
   Creates a pattern of drawings in which the tower grows by a layer of three each time. This strategy shows that the student recognises how the pattern grows, but needs experience in representing growth patterns with numbers. Use questioning, such as “can you think ahead to shape six. What will it look like?" to further prompt this thinking. 
   Draws a collection of squares arranged in an array but with no evidence of understanding the width and height of the tower. This indicates that the student needs experience in looking for organization (structure) in growing patterns.  
   
   Supporting activity:  
   Predicting ahead  
    

3. What will the twelfth shape in this pattern look like?  
   How many squares will be in the shape? Explain how you know.  
     
   
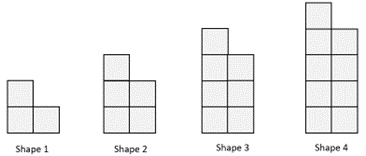
   Signs of fluency and understanding:  
   Recognises that the shapes are made up of a tower that is two squares wide with an additional square on the top left hand side. Explains that the twelfth shape will have a tower that has 12 x 2 = 24 squares and an extra square on top making a total of 25 squares.   
   Continues a table of values until the number of squares in the twelfth shape is found. Recognises that the pattern grows by two each time. Although this is a useful strategy, further development of functional thinking is needed.

   Shape number	1	2	3	4	5	6	7	8	9	10	11	12
   Number of squares	3	5	7	9	11							25

   
   What to notice if they don’t solve the problem fluently:  
   Creates a table of values and applies ratio thinking inappropriately. Explains that the fourth shape has nine squares, so the 12th shape has three times as many squares, 27. This indicates that the student needs experience with growth patterns where ratio thinking needs adjustment.  
   Unable to organise the pattern (structure the pattern) and therefore resorting to speculative drawing or guessing the number of squares. This indicates that the student needs further experience in looking for constant and changing features in growth patterns.  
   
   Supporting activity:  
   Predicting ahead by structuring  
    

4. This is the fourth shape in a pattern. What do you notice about the shape?  
   Draw the third and fifth shapes in the pattern, the shape before this one and the shape after.  
   Explain how you know what to draw.  
     
   
   Signs of fluency and understanding:  
   Sees structure in the shape, such as layers that decrease one square with each step up or columns that decrease by one square with each step to the right. Notices that the width and height of the tower are four and conjectures that the third and fifth shapes will have widths and heights of three and five. Draws the following shapes:  
     
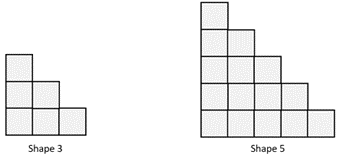
   Creates a pattern of shapes that uses the given shape and builds on and back in a consistent way, such as:  
     
   
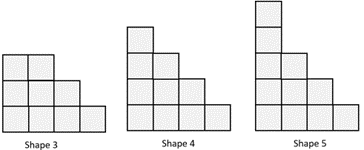
   What to notice if they don’t solve the problem fluently:  
   Cannot explain the way the shape is structured. Tends to see individual squares rather than spatial arrangements so finds it difficult to draw the next shape in the pattern. This indicates that the student needs experiences in looking for structure in spatial patterns and predicting ways that the spatial patterns can be extended.  
   Attempts to draw arrangements of squares that have some structural similarities to the given shape, such as layers or a staircase. May not be able to connect the width and height of the staircase with the pattern number. This indicates the student looks for structure in spatial patterns but needs support in noticing key features.  
   
   Supporting activity:  
   Creating patterns from a single shape