New Zealand Curriculum: Level 3
Learning Progression Frameworks: Geometric Thinking, Signpost 4 to Signpost 5
Target students
These activities are intended for students who can recognise and name two-dimensional (flat) shapes. Students should be able to sort two-dimensional shapes into classes using properties like the number of sides and angles, parallel and non-parallel sides, and symmetry. They should understand that some shapes are members of more than one class of shape. For example, the set of squares is included in the set of rectangles.
The following diagnostic questions indicate students’ degree of sophistication in classifying three-dimensional shapes by features, and then by properties. A feature is a perceptual (visual) characteristic, such as straightness of sides or pointiness of corners. A property is pattern or consistency that connects features, such as the solid has six sides that are all squares. (show diagnostic questions)
The questions should be presented orally and in a visual form, so the student can refer to them.
- Here are some pictures of three-dimensional (solid) shapes. Please tell me the name of each shape.

Why is the shape a ……?
Do you know something in the world that is a …….?
Note: Have students answer orally rather than in written form.
Signs of fluency and understanding:
Names all three shapes correctly using the mathematical words, cube, pyramid, and cone.
Explains some features of each shape, such as square faces, apex, straight edges, and gives a real-life object of that shape, such as ice cube, dice, Egyptian pyramid, icecream, or traffic cone.
What to notice if they don’t solve the problem fluently:
Provides their own name for the shapes, such as “a 3D triangle” for the pyramid. May be able to describe some features, such as “a round bottom” or “a sharp point.” This indicates the student needs experience with locating three-dimensional shapes in their environment and describing the properties of the shapes.
Supporting activity:
Finding three-dimensional shapes, identifying, and describing the features
- What three-dimensional shapes are in this picture?
Name each shape you find and say how you know what it is.

Signs of fluency and understanding:
Correctly identifies and names the cube, pyramid, cone, cylinder, and sphere. May also name some or all of the prisms or the octahedron.
Uses mathematical words to describe the properties of the solids.
For example:
Pyramid – square base, 4 triangular sides, apex.
Cube – 6 faces that are squares, 8 corners (vertices)
Sphere – no sides, a curved shape.
Cylinder – two circles top and bottom, a curved surface.
What to notice if they don’t solve the problem fluently:
Recognises that the shapes look like object in real life, such as the sphere is a ball, and the cylinder is a can. This indicates the student needs opportunities to learn the mathematical names for the three-dimensional shapes.
Know some mathematical names for the shapes, such as cone and pyramid, but cannot describe properties of those shapes. This indicates that the student needs opportunities to sort three-dimensional shapes by properties and to use mathematical words such as faces, vertices, edges, and surfaces to describe the properties.
Supporting activity:
Identifying and describing properties of three-dimensional shapes
- Cut out the shapes on the last page of the question sheet so they are each on a separate rectangular card. Note: If your school has a set of relational solids, you could use the 3D models rather than cards. Alternatively collect objects that are examples of the shapes, such as packets, balls, and blocks.
Sort these three-dimensional shapes so that the shapes that are the same are in the same set (group).
Signs of fluency and understanding:
Sorts the solids into categories (classes) based on common properties of the shapes. Explains the properties common to the shapes in each subset, such as:
“These shapes have curved surfaces. These shapes have flat faces. These shapes have a mixture of curved and flat surfaces.”
“These two shapes all have a single point at the top.”
“These shapes all have rectangular faces.”
What to notice if they don’t solve the problem fluently:
Unable to create subsets and identify the common features or properties. This suggests that the student needs further experience noticing similarities and differences between two or more shapes. This should draw on students’ everyday language and provide opportunities to learn topic-specific, mathematical vocabulary.
Creates subsets of shapes without credible commonality. This suggests that the student needs further experience with sorting items by given features progressing to sorting items by self-chosen features.
Supporting activity:
Sorting three-dimensional shapes by given properties
- Use the cards made from the last page of the question sheet or use real solid shapes if you have them (match the shapes in the sheet).
Sort these shapes into two groups, shapes that have vertices (corners) and those that have no vertices.
What can you say about all the shapes that have corners?
Re-sort the shapes in a different way. Make two groups; shapes that have any rectangular faces and those that have no rectangular faces.
What can you say about all the shapes that have rectangular faces?
Signs of fluency and understanding:
Sorts the shapes accurately using the criteria provided.
For the first sorting, strictly, the apex of the cone is a vertex. However, excuse the student not including a cone in the set of shapes with vertices.
For the second sorting, ignore the placement of the cylinder. The wrapping surface of a cylinder is a rectangle when laid flat though in three dimensions that wrapping is curved so cannot be a flat shape, like a rectangle.
What to notice if they don’t solve the problem fluently:
Unable to consistently sort shapes by either criterion. For example, may be confused between edges and vertices. This may indicate that the student needs further experience sorting three-dimensional shapes by given properties.
Difficulty interpreting drawings as representations of solid shapes. May be unable to visualize unseen parts of the shape or make incorrect assumptions. For example, the views of square-based and triangular-based pyramids are viewed a similar. This indicates that the student needs opportunities to draw three-dimensional solids and to use construction materials to build three-dimensional solids from drawings.
Supporting activity:
Sorting three-dimensional shapes by similarity and difference
- Someone put shapes that are the same into these two rings. (Point)
What is the same about the three-dimensional shapes in each ring?
There are three more shapes to sort. (Point to three shapes)
Which ring does each shape belong in? Explain why.
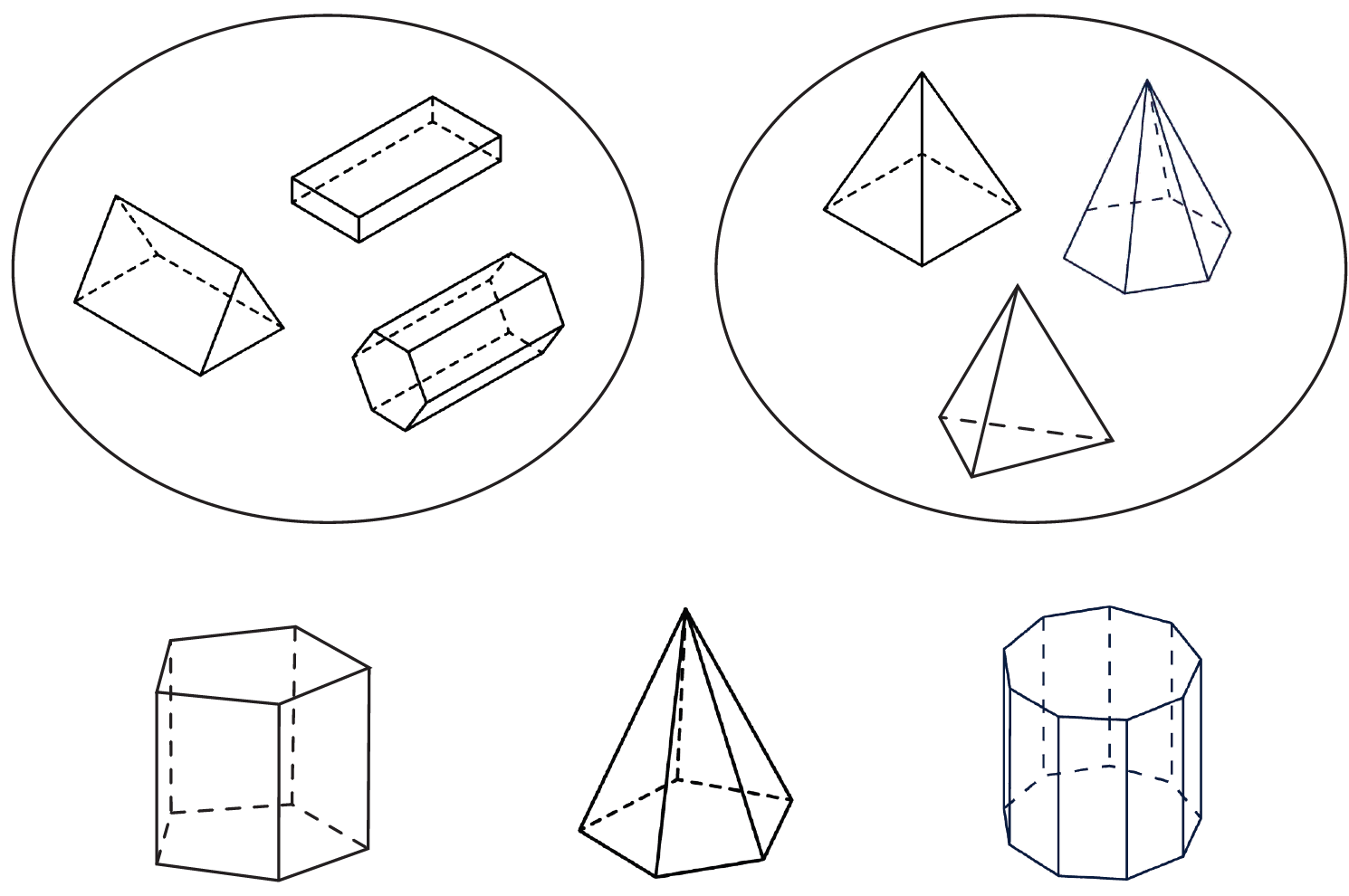
Signs of fluency and understanding:
Establishes similar properties in the shapes within each set. May know the mathematical names for the sets. The properties might include:
Left side (Prisms) – End faces that are the same, rectangular faces that wrap around the end faces, constant cross-section (the defining property of prisms).
Right side (Pyramids) – Apex at the top, triangular lateral faces (sides), base shapes (the source of a pyramid’s name).
Correctly locates the three additional shapes as below. Provides explanation of the location using defining properties. For example, this belongs in this set because it has a top point and triangular sides (faces).
What to notice if they don’t solve the problem fluently:
Unable to establish a legitimate criterion for inclusion in each set, so allocates the three shapes randomly. This indicates that the student needs further experience classifying three-dimensional shapes by properties, including finding examples and non-examples.
Supporting activity:
Classifying three-dimensional shapes
Teaching activities


