This problem solving unit is suitable for Level 5 (or Level 6) students.
In this problem solving unit, we look at the way numbers can be written as the sum of consecutive strings of whole numbers. The point of this unit is to give students a chance to
- see how mathematicians operate
- display ingenuity and creativity
- practice arithmetic in context
- learn what generalisations, extensions, conjectures, theorems, and proofs are
- see that some proofs are ‘nicer’ than others
- work through a completely novel situation and try to develop a mathematical theory around it
- Solve a mathematical problem.
- See how to generalise and extend a problem.
- Understand why and how mathematical statements may be justified.
- Work with others to solve a problem and generate new ideas.
Like all of the Problem Solving units, this one aims to introduce students to the underlying ideas of mathematics through a problem. The problem here requires a knowledge of arithmetic and the use of some algebra. In this unit we see how a mathematical theory might develop through experimentation, conjecturing, proving, generalising and extending.
This unit lies between the two problem solving units V-numbers and the Six Circles in difficulty. Students should try the V-numbers first and move on to Six Circles. Perhaps the three units could be spread over two years.
As with all of these units it is difficult to break the development here up into lessons as we can never be quite sure how any particular class will progress. This will depend both on their ability and on your scaffolding. The right question asked at the right time will enable more rapid progress. However, you don’t want to make it too rapid!; You would like most of the class to be able to follow what you are doing while not having to struggle too much to get a worthwhile distance into the problem.
Anyway, the sessions that we have used to set out this unit are definitely not of equal length. You may well want to run some sessions over into more than one lesson, while others may not take a whole lesson.
The W and worm problems develop from a particular example to an attempt to see a general situation. This is the course that all mathematics takes. So students here are getting an appreciation of the way that mathematicians work. It is important that they understand this and realise that what they are doing here is different from other mathematics lessons where they practice what someone else has produced. There is always the chance that they can find out something new during this process. (If they do, then we would like to hear about it. With their permission we would then like to share it with other users of the site.)
In view of what has just been said it is worth letting them know that mathematics develops roughly according to the following diagram.
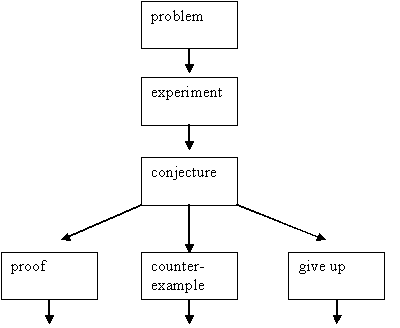
We have tried to give full background notes split up session by session. Please contact us if more details are required.
This problem is on the NRICH web site (www.nrich.maths.org). There students are able to manipulate the numbers on screen. Click here to go straight to the problem.
Background
First we start off with the problem.
Problem 1: Look at the W shape made by the circles below. Can you put each of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 into the circles below, so that the sum of the three numbers in each straight section of the W is 13?
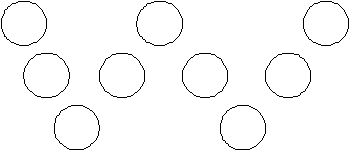
There are several ways to do this. We’ll show three methods that increase in level of sophistication.
Method 1: Guess and check.
There’s not much to say about this really. You just keep guessing and checking that the numbers in the straight sections add up to 13. If you do this systematically, then you’ll eventually get an answer.
How might you go about this systematically? Well, you could think about where the 9 might go. Because of the symmetry of the W shape and the fact that the numbers in the two end circles on each side can be swapped around, there are only four places to put the 9. Then think about what makes 13 with 9 and try to place those numbers. Then move on to 8.
While this is not a brilliant way to do this problem it does have some advantages. First it helps you to see what the problem is all about. It has to do with the numbers 1 through 9; some bits have to add up to 13; and no number can be used more than once. Second it might get you thinking about the fact that the number 13 is important. How can you get 13 with three numbers from 1 through 9?
Method 2: The idea of the last method about 13 can be used to produce a more efficient method. How can we make 13 using three numbers from 1, 2, 3, 4, 5, 6, 7, 8, and 9? We’ll list all the sums systematically below:
9 + 3 + 1; 8 + 4 + 1; 8 + 3 + 2; 7 + 5 + 1; 7 + 4 + 2; 6 + 5 + 2; 6 + 4 + 3.
The way to get this list is to start with the biggest number, 9, and see how you can make 13 using it. You can’t use 9 + 2 + 2 because every number has to be used at least once. So no number can be used twice.
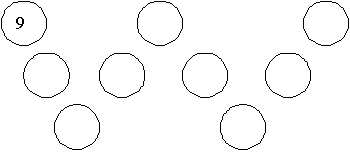
Diagram A
When you’ve completed the sums with 9, go down to the sums with 8. Then go to 7 and then 6. When you get to 5, you’ll see that 5 + 4 + 3 = 12. So we can’t get a new sum involving 5 that we haven’t already got. The same is clearly true for 4, 3, 2, and 1.
The advantage of this method is that we immediately see that 9 can’t be put in a circle that is on two straight sections of the W (a corner circle). If it could, then it would have to be in at least two of the sums in our list. So there are really only two places for the 9. We show these in the diagrams A above and B below.
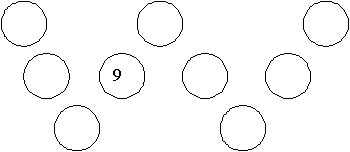
Diagram B
The problem now is where to put the 1 and the 3.
Consider Diagram A. If 1 is not used in the corner circle then we have only the following sums left in our list as we can’t use 1 again.
8 + 3 + 2; 7 + 4 + 2; 6 + 5 + 2; 6 + 4 + 3.
This means that we have to use either 8 + 3 + 2 or 6 + 4 + 3 next as 3 is in the corner. If we are using 8 + 3 + 2, then we can delete 6 + 4 + 3 from our list. That means that we have to use 7 + 4 + 2 and 6 + 5 + 2. But we can’t use the 2 three times!
So we have to use 6 + 4 + 3. But that means that 8 + 3 + 2 is struck from our active list as we can’t use 3 again. But that is a problem because now we can’t use 8 at all.
This means that in Diagram A, 1 has to be in the first corner. With 3 now gone from contention, our list for the final three sides is reduced to:
8 + 4 + 1; 7 + 5 + 1; 7 + 4 + 2; 6 + 5 + 2.
If we try 8 + 4 + 1, then 8 is in the middle and 4 is on the second corner. The only sum left with a 4 is 7 + 4 + 2. If you put 7 in the third corner, then you can’t use the 6. So 2 goes into the third corner. The final straight is taken up with 6 and 5. So we have the first answer that we show below.
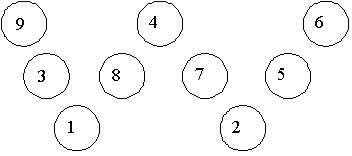
At this point you have to decide whether you have one or four or even eight answers. It depends on whether you allow the 3 and the 9 to be interchanged and the 5 and the 6 to be interchanged. And it also depends on whether you think that reflecting the W about an axis through its centre gives another answer. We prefer to say that these are essentially all the same. Once you have one you can easily get all of the others. So we are going to say that so far, we have only one answer.
This raises the question of whether once we have got one answer we should try to see if there are any more. Certainly it’s nice to know one way or the other, so we’ll keep on going.
Let’s now look at Diagram B. Again we will need to go systematically through it if we are to be sure not to leave anything out. So we either have the 1 in the first corner circle or the second corner.
If 1 is in the first corner, then we could have 8 + 4 + 1 or 7 + 5 + 1 along the first side. If we used 8 + 4 + 1, then the sums left are:
7 + 4 + 2; 6 + 5 + 2.
None of these has a 3 so we can’t continue past the second corner. So 3 is in the first corner. We therefore have 8 + 4 + 1 or 7 + 5 + 1 along the first side of the W.
If it’s 8 + 4 + 1, then we are left with only the 6 + 5 + 2 as one number has been used from all of the other sums. If 7 + 5 + 1 is on the first side, we are left with just two sums (8 + 3 + 2; and 6 + 4 + 3). Both of these has a 3 so both have to be used on the third straight.
It looks like (i) there is only one answer; and (ii) there ought to be a better way to settle this problem (maybe we should have given up when we found the answer from Diagram A).
Method 3: This is the case of the missing seven. If you think about it we can count the sums of the numbers in two ways. First we have four straights that each sum to 13. This gives us 4 x 13 = 52. Then we can add up the numbers form 1 to 9. This gives us 45. But we have missed something 52 – 45 = 7. Where did the missing 7 go?
Of course, we forgot to add in the corners. 52 = 45 + the numbers used twice in the corners. So the corners must give us the extra 7. There are three corners, so we need to find all of the ways that three numbers can add to 7. Ah! Fortunately 7 is small. It can only be obtained by 1 + 2 + 4! So 1, 2, and 4 go in the corners. But that means we still have several cases. Unless … Unless you note that if 1 and 2 were in adjacent corners we would need a 10 to make 13 for that piece of straight. So, without loss of generality (i.e., because of the symmetry of the W), we can start with the situation in Diagram C.
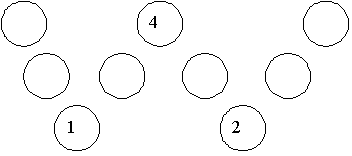
Diagram C
But now life is all down hill. It’s clear that we have 8 between the 1 and the 4, and it’s clear that we have 7 between the 2 and the 4. There is only one sum with a 9 and that has a 1 too. So the first straight is 9 + 3 + 1. The last two numbers follow by elimination of all the others that we have used.
Don’t you like that method a lot better?
Teaching Sequence
- Introduce the problem and make sure that the class understands it. Let them go off in their groups with the instruction that they are to find as many answers as they can and to use as many methods to solve the problem as they can.
- Go round the groups and check on their progress. Help those groups that are struggling with an appropriate hint. For those groups that have found an answer, suggest that they try another method.
- After 20 minutes or so, bring the whole class together to report on what they have found. This may help some of the struggling groups.
- Let the groups continue working.
- Bring them together near the end of the session to discuss methods of solution and answers. In particular discuss whether there is really only one answer or whether there are eight. Allow individual students the chance to tell the others what they have found. Make sure that different students are given this opportunity. Each student’s contribution should be respected by the others.
- Give the students the time to put the results of this session into their books.
(If necessary, this problem might be completed for homework.)
Session 2
In this session students get a chance to push Problem 1 a little further by extending it in a special case.
Background
We now start to extend Problem 1. This is the strategy that we have used in V-numbers and the Six Circle problem.
Problem 2: Look at the W shape made by the circles below. Can you put each of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 into the circles below, so that the sum of the three numbers in each straight section of the W is 14?
Encourage the class to think Method 3. In that case, we need to worry about 4 x 14 – 45 = 11. The corners add to 11. This time, unfortunately, there is more than one way to make 11. Let’s be systematic and see how many there really are.
1 + 2 + 8; 1 + 3 + 7; 1 + 4 + 6; 2 + 3 + 6.
Four isn’t too bad, especially as … But we’re getting ahead of ourselves.
Case 1, 1 + 2 + 8: Since 1 + 2 + 11 = 14, we have to have the 1 in the first corner, the 2 in the third corner and the 8 in the second corner. We show this in Diagram D.
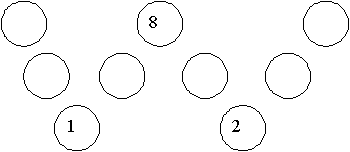
Diagram D
It’s easy to fill it up from here.
Case 2, 1 + 3 + 7: Again the 1 and the 3 can’t be adjacent. So we get the situation int Diagram E below.
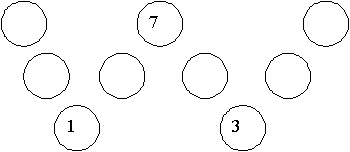
Diagram E
Finishing that off should be straightforward.
Case 3, 1 + 4 + 6: In this case we can’t have 4 and 6 adjacent as they require another 4. So here we go with Diagram F.
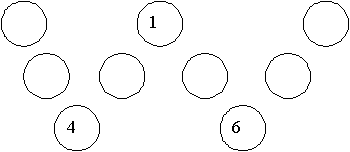
Diagram F
You can quickly finish that.
Case 4, 2 + 3 + 6: And 2 and 6 can’t be adjacent (they would need another 6). So we have Diagram G that is easy to complete.
.gif)
Diagram G
So we have four answers to Problem 2.
Teaching sequence
-
Remind the class of Problem 1. Get them to say what they recall from the last session. Especially remember the techniques that they used to solve Problem 1. Discuss with them how the problem might be extended or generalised. Make sure that Problem 2 arises in these discussions.
-
Tell them that in this session they are going to solve Problem 2.
-
Let them work in their groups on Problem 2. Wander around the groups helping them to recall points from the last session, giving them hints for the present problem, and suggesting new directions for the prompt finishers.
-
Bring the class together to discuss their answers. Let individuals report to the class what they have found. Make sure that different students get a chance in this discussion from those who were heard in the last one.
-
Give them the opportunity to think about where the W problems might go next.
-
Allow the students time to record in their books what has been done.
(You might let them try to find some extensions for homework.)
Session 3
In this session, we open up the two problems that we have worked on to the case where there is no restriction on the sums on each of the straight sides. This will lead to a general solution to the W problem.
Background
We now extend Problem 1 even more. This is the same strategy that we have adopted in V-numbers and the Six Circle problem.
Problem 3: Look at the W shape made by the circles below. Can you put each of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 into the circles below, so that the sum of the three numbers in each straight section of the W is the same?
The question really is this, we have seen how to solve the W problems for a sum on the straight sections of 13 and 14, but what other straight side sums are possible?
This can be done experimentally but the algebraic approach is the most efficient.
Let the sum of the three numbers on the straight pieces be s. Then
4s = 45 + (sum of the corners).
First notice that the sum of the corners lies between 6 (1 + 2 + 3) and 24 (7 + 8 + 9). But we can cut this down quite a lot by noticing that the left side of the last equation is divisible by 4. So the right hand side has to be too. This means that we only need to take the sum of the corners that, when added to 45 gives a multiple of 4.
The required corner sum are 7 (s = 13); 11, (s = 14); 15 (s = 15); 19 (s = 16); and 23 (s = 17). We have already worked the problem out for s = 13 and s = 14, so we now only have to get s = 15, 16 and 17.
Case 1, s = 15: One way that the corners could sum to 15 is if we had 3 + 5 + 7. But if we put 3 and 5 in two adjacent corners we would require the 7 in the middle of that straight piece. That means that we would have to use 7 twice – once in a middle circle and once in a corner one. We can’t use any twice, so this is not possible. But the same argument applies no matter what the three numbers are that we add to make 15. We simply can’t have the corners and the straight summing to 15. There are no answers here.
Case 2, s = 16: Using the Method 3 we get four answers.We list them below:
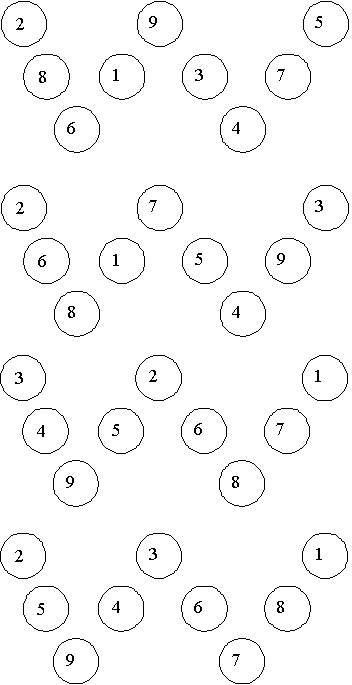
Case 3, s = 17: Using Method 4 we get one answer. We list it below.
.gif)
Having got this far you might just stop and relax in awe at what you have done but there is one more thing to note. Did you notice that there is only one answer for s = 13 and one for s = 17. There are four answers for s = 14 and four for s = 17. Is this a coincidence?
Of course not! But what is the relation between them? Well try replacing the number x in the s = 13 answer by the number 10 – x. What happens? Why? Then try replacing the number x in s = 14 answers by the number 10 – x. What happens? Why?
Suppose that p + q + r = 13. Then (10 – p) + (10 – q) + (10 – r) = 30 – (p + q + r) = 30 – 13 = 17!
Suppose that p + q + r = 14. Then (10 – p) + (10 – q) + (10 – r) = 30 – (p + q + r) = 30 – 14 = 16!
Suppose that p + q + r = 16. Then (10 – p) + (10 – q) + (10 – r ) = 30 – (p + q + r) = 30 – 16 = 14!
Suppose that p + q + r = 17. Then (10 – p) + (10 – q) + (10 – r ) = 30 – (p + q + r) = 30 – 17 = 13!
So the x to 10 – x map, sends us between 13 and 17 and between 14 and 16. It is in fact, a one to one map between both pairs. This means that we needn’t have done the work above for s = 16 and s = 17. We could have deduced it straight from the x to 10 – x map! But how were we to know that beforehand?
Teaching Sequence
-
Recall what has occurred in each of the last two sessions. Give the class the opportunity to contribute as much as possible. Recall, or lead them to suggest, any extensions of Problems 1 and 2.
-
Let the class know that their task for this session is to solve Problem 3. Discuss what this means. Even talk about how they might go about it. Underline one of the important principles of problem solving “Have I seen a problem like this before?”
-
Set them to work in their groups. Walk around to give assistance. You may need to encourage some of them into thinking algebraically. Hear their justifications for what they have found. Get them to write down their work in preparation for presenting it to the whole class.
-
There is more than one way to solve the problem. The method that we have given in the Background is probably the most efficient but other ways are possible. Show the students that any correct argument is equally valid. However, let them see that some routes take less time than others. Try to get the class to appreciate the algebraic method as being quite efficient.
-
Make sure that somewhere during the session you introduce the idea of changing the numbers x to 10 – x. (It is something that you could hint at to the students who finish early, either in this session or the last one.) What is the advantage of this?
-
After a while bring the class together and allow students to present their work. This needs to be done in a supporting atmosphere where everyone is heard and everyone’s views are treated with respect.
-
The edited work of the groups should be written down as a record of what happened.
Session 4
In this session we look at a new problem that is similar to the ones that we have been working on for the last three sessions. The students should have a chance to solve this with little prompting.
Resources
It may help your students to have some worm shapes available to start them off. You can find these in Copymaster 2.
Background
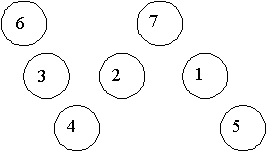
Problem 4: Look at the worm shape made by the circles below. Can you put each of the numbers 1, 2, 3, 4, 5, 6, 7 into the circles below, so that the sum of the three numbers in each straight section of the worm is the same?
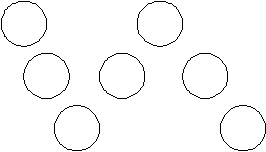
If we use Method 3 of Session 1, we see that 3 times the sum of each straight section is equal to the sum of the numbers from 1 to 7 plus the two numbers in the corners. In other words,
3s = 28 + (sum of corners).
But the sum of the numbers in the corners lies between 3 (if the corners are 1 and 2) and 13 (if the corners are 6 and 7). On the other hand, the left side is a multiple of 3. So 28 + (sum of corners) has to be a multiple of 3. This means that the sum of the corners is either 5, 8, or 11. We use each of these in turn to get seven possible answers.
Case 1, sum of corners = 5: We can get 5 in two ways: 1 + 4 and 2 + 3. Each of these gives an answer. We show these below. They are obtained in the usual way once we notice that if the sum of corners = 5, then s = 11.
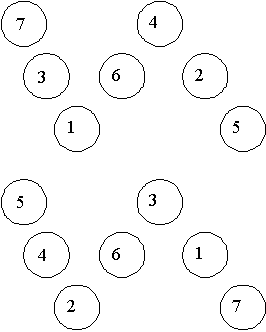
Case 2, sum of corners = 8: We can get 8 in three ways: 1 + 7; 2 + 6; and 3 + 5. Each of these gives an answer. We show these below. They are obtained in the usual way once we notice that if the sum of corners = 8, then s = 12.
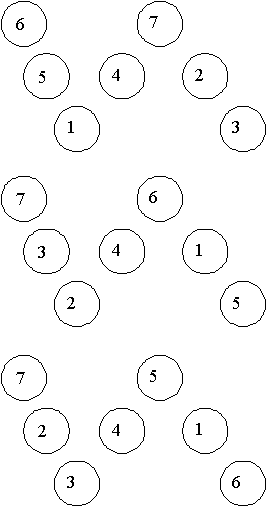
Case 3, sum of corners = 11: We can get 11 in two ways: 4 + 7 and 5 + 6. Each of these gives an answer. We show these below. They are obtained in the usual way once we notice that if the sum of corners = 11, then s = 13.
.gif)
But hang on; we should have been able to save ourselves some time here. Remember the trick of changing x to 10 – x in the W problem? Surely the equivalent here is changing x to 8 – x. Check it out. It will change the Case 1 answers to Case 3 and vice versa. (Unfortunately it will only change the case 2 answers to themselves. But some help is better than none.)
Just to make sure it works let p + q + r = 11. Then (8 – p) + (8 – q) + (8 – r ) = 24 – (p + q + r) = 24 – 11 = 13. You can do the rest.
Teaching Sequence
-
Revise what has happened in the last three sessions. Get the students to recall the problems the method of solutions and the answers. Remind them of the basic principle “Have I seen a problem like this before?”
-
Pose Problem 4 and without any more discussion set them to work in their groups.
-
Walk among the groups giving hints and keeping students on track. Watch for opportunities to extend the more able students without giving away the ideas of Session 5.
-
Give students who haven’t presented their work before the chance to do so in front of the whole class.
-
Get the students to summarise their work in their books.
Session 5
This is potentially a longer session than the other four.
Background
In both the W of Session 1, 2 and 3 and the worm of Session 4 we have seen that we can get answers with using consecutive numbers. What sets of numbers can be used with the W and the worm so that the straight line segments in each case add up to the same?
Case 1, the worm: Label the circles as shown below.
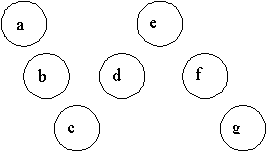
Now since a + b + c = s = c + d + e = e + f + g, then we can simplify a bit to give
a + b = d + e; and c + d = f + g.
Any set of seven numbers that satisfies the equations above will give an answer to the worm problem. However, it’s not easy to test a set of seven numbers to see whether it satisfies the two equations.
Case 2, the W: Label the circles as shown below.
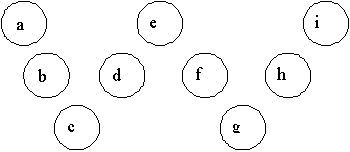
Doing the algebra here we get
a + b = d + e; c + d = f + g; and e + f = h + i.
Any set of nine numbers that satisfies the equations above will give an answer to the W problem. However, it’s not easy to test a set of nine numbers to see whether it satisfies the three equations.
Teaching Sequence
- Recall the worm problem. You used the numbers 1 to 7 there. What other numbers could you use and still have the problem work. In other words, what sets of 7 numbers can you find, so that the three numbers on the straight pieces of the worm all add up to the same sum?
- Experiment in class. Let students suggest various numbers and then try to see if they work or not. Any sets that you can’t get to work immediately put to one side. It’s not always easy to see how to manipulate the numbers even if they do fit the worm in the way that we are asking.
- Give the students time in their groups to find as many sets as they can. While they are doing this, they should be looking for patterns.
- Once they have all get a few sets that work and some that they think don’t work, encourage them to try to use an algebraic approach.
- Come together and discuss the algebraic solution of the Background above. Let them think about how they would tell if a given set of numbers satisfies that rule. Test the sets that you had put to one side as being hard to see if they worked or not.
- Repeat steps 1 to 5 above with the W problem.
In this final session we are aiming to completely solve the two problem ideas that we have been working on in the last four sessions. We want students to think about what sets of numbers could fit into the W or worm set ups so that the sums of the numbers on each straight piece were equal.