V-numbers

Lesson Sequence

Session 1

Background

First we start off with the problem on which this whole unit is based.

Basic Problem: Can you put the numbers 1, 2, 3, 4, and 5, one per circle, so that the numbers on the left hand side of the V add up to the same as the numbers on the right hand side of the V?

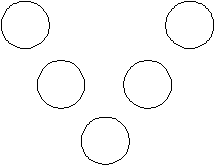
Before you take the problem to the class it’s worth giving it a bit of thought. There are a few things that need to be considered.

1. What constitutes an answer? For instance, are the two answers below the same or different?

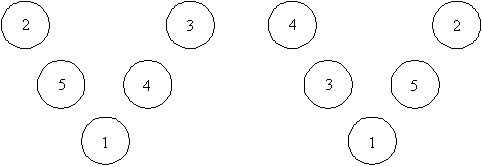
It doesn’t matter whether you decide that they are essentially the same or that they are different. Let students put forward their ideas and then make a class decision. Whatever decision they make will need to be maintained through the rest of the unit. In this unit we will assume that they are the same. This, of course, has the advantage of enabling us to write fewer diagrams. But it is probably the way that mathematicians would go as it means that they can pack several pieces of information into one. After all, once this decision has been made, four answers are encapsulated in one. All of these four ‘different’ answers can be recouped when, or if, needed.

2. How many different answers exist?

Given the decision that we made in (i) there are only three answers. (If the other decision is made there will be 12.) These will have 1, 3 and 5, respectively, in the bottom circle of the V.

3. Why are there no other answers? Why cannot 2 or 4 be in the bottom circle?

Many students will say ‘it’s obvious’ or something similar. But don’t accept this. Why is it obvious? Get them to try to explain why they think it is clear.

There are at least three ways of doing this. First, if you put 2 in the bottom circle, then 1 has to go somewhere. If you try successively to put 3, 4 and 5 with 1, no answer is possible – there is no way of balancing the numbers on either side of the V.

Second, 1 + 3 + 4 + 5 = 13. If these numbers are to be used in an answer, then 13 would have to be even as half must go on one side of the V and half on the other.

Third, 1, 3, 4, and 5 contains three odd numbers. So one must go on one side of the V and two on the other. But then one side of the V must have an odd number for it’s sum and the other an even number. An even number can’t equal an odd number. So there is no way to get an answer here.

Exactly the same methods can be used if 4 is in the bottom V circle.

Now you’re ready to take it to the class.

Teaching Sequence

1. Treat this like any of the Problem-solving lessons that can be found elsewhere on this site. Introduce the problem and discuss it to ensure that all of the students understand what the question is asking and how it might be tackled. Then give students the chance to solve the problem in groups of 2 to 4. They may find Copymaster 1 useful for them. It’ll help them to keep their results arranged in a tidy fashion.
   
   As groups come up with answers, encourage them to find more answers. When they think that they have found all of the possible answers, encourage them to prove that the answers that they have found are the only ones that exist. Give everyone a chance to make some progress on the problem. During this phase of the lesson, you may find it necessary to discuss different parts of the development of the problem. Allow them to make major decisions for themselves, such as what constitutes an answer.
2. Have a class discussion on the results of the exploration above pulling in all of the points (i), (ii), (iii) above. The reason for this is to make sure that everyone knows that there are precisely three answers; that most students have a chance to contribute; and that some discussion takes place on the proof of (iii) above. As far as the proof goes, let the students discuss it until they are convinced that it works.
3. Get each student to write up their solution to the problem and then share it with someone else.
4. Finally have a think-tank session to generate ideas for the next lessons. Think of the different properties that this problem has and see if you can produce similar ones. (In what way can you get more problems from the basic one?)
   
   As you try more of these units we hope that you will find it easier to produce generalisations and extensions.
   
   Note that you may well think of ideas that we do not cover here. It is important that you follow them through to see where they lead. If you get some nice results please let us know so that we can tell others. We’ll certainly acknowledge anything of yours that we put on the web.

Session 2 and 3

Background

To help us with the rest of the unit, we define a V-set to be a set of five distinct numbers that can be put into the five circles that form a V, so that the sum of the numbers on the left hand side of the V is the same as sum on the right hand side. Definitions like this are very important. It’s a real pain having to say a “set of five numbers that can be put into the five circles that form a V, so that the sum of the numbers on the left hand side of the V is the same as sum on the right hand side” every time.

What we try to do now is to see what has happened with the V-set {1, 2, 3, 4, 5} and see if we can find other sets that have any of the properties of that set. So let’s rehearse what we have found with {1, 2, 3, 4, 5} and then see if we can find other sets like it. At this stage anything you can think of will do, no matter how basic you think it might be. We can only think of three things at the moment (A, B and C below – you may be able to think of other ideas). Let’s see how far they take us.

1. {1, 2, 3, 4, 5} is a V-set.
2. {1, 2, 3, 4, 5} is a V-set in three ways.
3. There are two circles on each of the ‘arms’ of the V.

Possible ideas:

A1: What other sets are V-sets?
A2: Are there any sets that are not V-sets?
A3: Can we find all V-sets?
B1: What sets are V-sets in three ways?
B2: What sets are V-sets in just two ways?
B3: What sets are V-sets in just one way?
C1: What if there are three circles on each ‘arm’?
C2: What if there are two circles on one ‘arm’ and three circles on the other?
C3: Put as many circles on each side as you like.

You may find that they quickly see the following conjectures (guesses – see Problem Solving Background).

Conjecture A1: Any set of 5 consecutive numbers is a V-set.

Conjecture A2: Any set of 5 numbers in arithmetic progression (there is a common difference between each pair of consecutive numbers) is a V-set.

This conjecture is a generalisation of Conjecture 1 as the common difference between each pair of consecutive numbers is 1.

Conjecture A3: Any V-set is an arithmetic progression.

It would be nice to settle Conjectures A2 and A3 as if they were true they would tell us all there is to know about V-sets. Unfortunately, as we shall see, Conjecture A3 is false: there are V-sets that aren’t arithmetic progressions.

Proof of Conjecture A1: Any set of 5 consecutive numbers consists of 1, 2, 3, 4, 5 plus some constant. So simply add that constant to 1, 2, 3, 4, 5 as they are in any one of the three answers we know and that will give us sums on each arm of the V that are the same. So any set of 5 consecutive is a V-set.

Proof of Conjecture A2: Any set of 5 numbers in arithmetic progression is some multiple of 1, 2, 3, 4, 5 plus some constant. (For instance, 7, 10, 13, 16, 19 is three times 1, 2, 3, 4, 5 plus 4.) So if we take an answer for 1, 2, 3, 4, 5 and multiply by the appropriate multiple and add the given constant, we get the numbers on the two sides of the V adding got the same sum.

Counter-example to Conjecture A3: {1, 2, 3, 6, 7} is a V-set (with side sum 10) and the numbers 1, 2, 3, 6, 7 are not in arithmetic progression.

So we need another idea to be able to find out what sets are V-sets.

The best we can do is so simple that some of your students may not like it or may look for something more complicated.

Conjecture A4: A set is a V-set if the sum of any two of the numbers is the same as the sum of any two of the remaining numbers.

Proof: Suppose that x + y = r + s and that the fifth number is m. Then we can put the five numbers into the V shape with m at the point, x and y on one side and r and s on the other. Clearly, m + x + y = m + r + s and we are done.

But this gives us a complete characterisation of V-sets.

Theorem A: A set of five numbers is a V-set if and only if the sum of any two of the numbers is the same as the sum of any two of the remaining numbers.

Proof. Suppose that five numbers has the property in the statement of the Theorem. Then they form a V-set by the proof of Conjecture A4. On the other hand, if five numbers are a V-set, then three of them a, b, c (b and c are on one side of the V) add to the same as a, d, e (where d and e are on the other). So b + c = d + e.

This theorem tells us all about V-sets.

Teaching Sequence

1. First continue the discussion from Session 1 and see what ideas (like the 9 above) your class can come up with. In the beginning, when they have had little practice doing this, they may need some help finding ideas. Hopefully they’ll get better as time goes on.
2. Let the class decide which of the ideas they have come up with they want to tackle. If they are novices at this game we suggest that each group tries the same idea. If they have been doing this sort of thing for a while you may want to let each group try whatever idea they like or even several ideas simultaneously. You will find that some ideas are perhaps more natural to try first. For this reason we’ll tackle A1 and A2 now. Hopefully there are advantages in trying two problems at once. (However, we’re going to consider them all at some point so don’t feel forced to follow the order we do things here.)
3. Talk about A1 and A2 with the class and then send the groups off to see what progress they can make. Get them to find as many V-sets and non V-sets as they can. Let them report back as they get success. Put up lists of V-sets and non V-sets on the board as they produce them.
4. Is there a pattern with V-sets? Can you look at any set of 5 distinct elements and tell whether or not it is a V-set? Follow the direction that they take and help them with their conjectures. However, insist that they justify any claims/conjectures that they make. (In the background material we show how to justify claims/conjectures. It is not enough to say that every example we have found so far works.)
5. You will need to judge how the class is going at this point. In this lesson, if they are able to get as far as showing that all arithmetic progressions form a V-set they have done well. It is likely that some students will go ahead or in different directions. Keep the average students as much together as possible and let others ‘do their own thing’. You can talk to these students in their group and keep them on track.

Towards the end of the Session 3, discuss the conjectures and their proofs. You might also show everyone (if one group has found the answer for themselves let them show the others how it works) the complete solution. This produces the answer to Conjecture A4.

Let the students discuss some of the proofs in order to make sure that they understand what is going on. Give everyone the chance to write up at least one of these proofs.

Session 4 and 5

Background

The big thing about our problem solving units is that if students are at sea by the end of one lesson, they can pick up and start again in the next. In the previous lesson we found out all there is to find about V-sets (or did you find more?). Here we look more carefully at deeper properties that not all V-sets possess. We do this by using the ‘B’ ideas from above. Recall that these are:

B1: What sets are V-sets in three ways? (Call these V(3)-sets.)
B2: What sets are V-sets in just two ways? (Call these V(2)-sets.)
B3: What sets are V-sets in just one way? (Call these V(1)-sets.)

What happens here is based very much on what happened in the last two sessions. Remind the class that the sets of numbers we are talking about here have two numbers whose sum is the same as some other two numbers in the set.

Here are some conjectures.

Conjecture B1: V(1)-sets are V-sets where there are a pair of numbers whose sum is the same as some other pair numbers in the set and these two pairs can be found in only one way.

Conjecture B2: V(2)-sets are V-sets where there are a pair of numbers whose sum is the same as some other pair numbers in the set and these two pairs can be found in exactly two ways.

Conjecture B3: V(3)-sets are V-sets where there are a pair of numbers whose sum is the same as some other pair numbers in the set and these two pairs can be found in exactly three ways.

This is fine but in some ways these are just different ways of stating the definitions of V(1), V(2) and V(3). So what do these sets actually look like?

Another conjecture that some of your students may get to before these is:

Conjecture B4: A set of numbers forms a V(3)-set if and only if its numbers are in arithmetic progression.

If this is correct this will explain how arithmetic progressions fit into the picture.

But around about here we are in algebra territory. From now on any proof will require some knowledge of algebra so you will need to decide whether your class can get this far.

Conjecture B5: A set of numbers forms a V(1)-set if and only if its numbers a, b, c, d, e are such that (i) a < c + d – e < c < d < e and c + d < e; (ii) c + d – e  < b < c < d < e and c + d < e; (iii) b + d – e < b < c < d < e and b + d < e; (iv) b + c – e < < b < c < d < e and b + c < e; or (v) b + c – d  < b < c < d < e and b + c < d.

Conjecture B6: A set of numbers forms a V(2)-set if and only if its numbers are such that …

In the last conjecture there are several conditions that have to be satisfied. We leave you to think about what these might be.

Proof of Conjecture B1: If the set is a V-set it has to have that property with two pairs of numbers. If that property holds there can be only one answer to the V problem.

The proofs of Conjectures B2 and B3 follow similarly.

Proof of Conjecture B4: If the set of numbers is in arithmetic progression then there have to be three answers. These model the three answers we found in Session 1 and the proof follows by the proof of Conjecture A2.

Let the V-set be {a, b, c, d, e}. Then there have to be equations that might be satisfied. These are (with the number at the point of the V before the colon):

a:  b + e = c + d   … (1);         
b:  a + e = c + d   … (2);
c:  a + e = b + d   … (3);
d:  a + e = b + c   … (4);
e:  a + d = b + c   … (5);

Note that to get the pairs of numbers required by Theorem A, one of the pairs must have smallest and the largest number.

Note that (1) and (2) can’t both be true as this implies that a = b; that (2) and (3) can’t both be true as this implies that b = c; that (2) and (4) can’t both be true as this implies that b = d; that (3) and (4) can’t both be true as this implies that c = d; that (4) and (5) can’t both be true as this implies that d = e.

So if (2) holds then (1), (3) and (4) cannot hold. This means that only (2) and (5) hold and so there are only two answers here. So (2) must be false. Similarly (4) can’t be true. So only (1), (3), and (5) are true and these give the only three answers.

Solving (1), (3) and (5) gives a, b, 2b – a, 3b – 2a, 4b – 3a. This is an arithmetic progression where4 the first term is a and the common difference is b – a.

The proofs to Conjectures B5 and B6 follow similarly.

Teaching Sequence

1. Remind students about the V-sets and what they did in the last lesson. Especially point them to the Theorem that was proved about all V-sets. To go further, we have to go back again to the experimental stage. Discuss the ideas with the class and send them off in their groups to find as many examples as you can of V-sets that have one, two and three answers.
2. As they produce examples, write them on the board so that they can all see what they look like. (Make sure that all claims are checked by other groups.)
3. When a reasonable number of examples of each type have been found, set the class to work to see if they can come up with conjectures as to which V-sets have which possibilities.
4. Discuss the conjectures that they suggest. Test them to see if the class can find any counter-examples.
5. Let the students try to prove any of the conjectures. Have a reporting back session to check out the proofs. Make sure that the proofs are discussed so that everyone understands them.
6. Give everyone the chance to write up at least one of these proofs.

Homelinks

This week in class we have been looking at V-sets. Your student will tell you what these are and some of what we did with them. We would like you to work together with them in something similar.

Can you put the numbers 1, 2, 3, 4, 5, 6 and 7, one per circle, so that the numbers on the left hand side of the V add up to the same as the numbers on the right hand side of the V?